
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон сохранения энергии для системы материальных точек. ⇐ ПредыдущаяСтр 3 из 3 Можно было бы рассмотреть и систему невзаимодействующих точек. Очевидно, что в этом случае можно просуммировать уравнения (46) и (47) написанные для каждой из частиц и получить закон сохранения в виде
Но вообще говоря большого смысла во введении такой суммарной энергии не взаимодействующих материальных точек нет. Это просто следствие того, что есть закон сохранения для каждой из материальных точек. Более важным является закон сохранения для системы материальных точек, которые взаимодействуют между собой. Для начала рассмотрим систему из двух материальных точек, которые взаимодействуют с помощью консервативных сил, задаваемых потенциальной энергией
Изменение полной кинетической энергии, складывается из изменения кинетической энергии каждой из частиц. Изменение же потенциальной энергии данной частицы равно соответствующей работе:
Если учесть, что
Дальнейшее упрощение выражения для полной работы получится, если рассмотреть приращения радиус-векторов в системе отсчета с центром, совпадающим с точкой 2. В таком случае радиус вектор
Но тогда:
И суммарная работа равна:
Мы получили, что суммарную работу можно посчитать в системе, где одна из частиц покоится. Но именно так мы и считали работу для одной частицы в поле консервативных сил. Естественно, что величина разность радиус-векторов двух точек не зависит от того, в какой системе координат эта разность вычисляется (В системе отсчета, где одна из точек покоится или в какой-то другой). Окончательно выражение для баланса энергии двух точек выглядит следующим образом: 
здесь верхние индексы (in) и (out) относятся к начальному и конечному состоянию соответственно. Случай, когда система состоит N частиц, попарно взаимодействующих друг с другом посредством консервативных сил сводится к рассмотренному, поскольку можно последовательно рассмотреть взаимодействие каждой пары частиц. В результате приходим к тому, что выражение для полной энергии такой системы дается выражением:
При написании этого выражения мы учли также, что на систему могут действовать внешние поля задаваемые потенциалами
Где
Здесь
Таким образом, представление о внешних полях является приближенным, но точность такого приближения может оказаться очень и очень высокой. Так, например, если прыгун весом 80 кгпрыгает на высоту1 м, тосмещение центра Земли конечно не нужно учитывать. Больше того, глупо даже пытаться это делать. А все-таки, каким будет смещение центра Земли в этом случае? Вспомним определение центра масс системы и запишем его для двух положений: прыгун на Земле и на высоте 1 м:
Тогда изменение положения радиус-вектора Земли равно:
Очевидно, что смещение Одно замечание по поводу законов сохранения. Различные законы сохранения возникают не только в механике, но в очень многих областях, для которых может возникнуть необходимость проводить расчеты. Самый простой пример из химии: горение водорода в кислороде:
Очевидно, что в этой реакции сохраняются следующая суммы:
При этом В заключение рассмотрим вопрос о преобразовании энергии системы при переходе из одной системы отсчета в другую. Т.ею при преобразованиях вида:
При этом скорость, как мы уже обсуждали, преобразуется по следующей формуле:
Пусть штрихованная система является системой центра масс. Это значит, что импульс системы для штрихованных скоростей равен нулю:
Найдем связь между кинетической энергией в системе центра масс и в системе, которая движется относительно системы центра масс со скоростью
Если учесть (67) то получим связь между кинетическими энергиями в рассматриваемых системах:
Эта связь называется теоремой Кёнига. Поскольку потенциальная энергия не зависит от системы отсчета, то можно написать:
Отсюда следует, что механическая энергия системы имеет наименьшую величину в системе центра масс. |
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 335. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
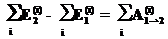 ,
,
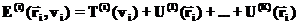 ,
,
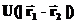 . Введем кинетическую энергию двух частиц, которая просто равна сумме кинетических энергий каждой из частиц.
. Введем кинетическую энергию двух частиц, которая просто равна сумме кинетических энергий каждой из частиц.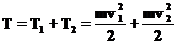 ,
,
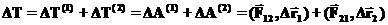
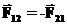 (третий закон Ньютона), то можно переписать это уравнение в более удобном для исследования виде:
(третий закон Ньютона), то можно переписать это уравнение в более удобном для исследования виде: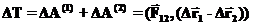
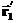 первой точки в этой системе дается выражением:
первой точки в этой системе дается выражением: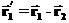
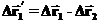
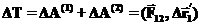
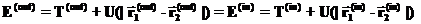 ,
,
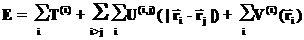 ,
,
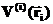 для каждой из частиц системы. В самом общем виде закон изменения энергии для системы взаимодействующих частиц можно записать в виде:
для каждой из частиц системы. В самом общем виде закон изменения энергии для системы взаимодействующих частиц можно записать в виде: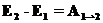 ,
,
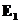 и
и 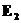 — полная энергия системы (56) в состояниях (1) и (2) соответственно, а
— полная энергия системы (56) в состояниях (1) и (2) соответственно, а 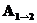 работа, совершаемая неконсервативными силами над всеми телами системы. Если неконсервативных сил нет, то, как видно из (57), полная энергия системы сохраняется. Здесь уместно сделать замечание о внешних полях. Такие поля создаются телами, которые мы не включили в нашу систему. В этом курсе мы рассматриваем только взаимодействия, которые сводятся к парным (между двумя материальными точками) и центральный характер. Такие взаимодействия задаются потенциалами, зависящими только от модуля радиус-векторов взаимодействующих частиц:
работа, совершаемая неконсервативными силами над всеми телами системы. Если неконсервативных сил нет, то, как видно из (57), полная энергия системы сохраняется. Здесь уместно сделать замечание о внешних полях. Такие поля создаются телами, которые мы не включили в нашу систему. В этом курсе мы рассматриваем только взаимодействия, которые сводятся к парным (между двумя материальными точками) и центральный характер. Такие взаимодействия задаются потенциалами, зависящими только от модуля радиус-векторов взаимодействующих частиц: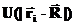
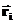 — радиус-вектор i-ой частицы рассматриваемой системы, а
— радиус-вектор i-ой частицы рассматриваемой системы, а 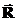 — радиус вектор частицы, не включенной в нашу систему, и которая создает внешнее поле. Если смещение внешней частицы за счет взаимодействия пренебрежимо мало (ну скажем, эта частица слишком тяжелая), то в таком случае потенциальная энергия зависит только
— радиус вектор частицы, не включенной в нашу систему, и которая создает внешнее поле. Если смещение внешней частицы за счет взаимодействия пренебрежимо мало (ну скажем, эта частица слишком тяжелая), то в таком случае потенциальная энергия зависит только 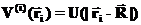 ,
,
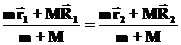 ,
,
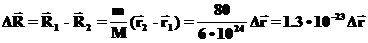 ,
,
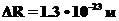 учитывать не нужно и бессмысленно. Размер атома в
учитывать не нужно и бессмысленно. Размер атома в 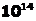 раза больше, т.е. никакого смещения нет. Таким образом, хотя понятие внешнего поля вводится на как некоторое приближение, такое приближение по сути является точным.
раза больше, т.е. никакого смещения нет. Таким образом, хотя понятие внешнего поля вводится на как некоторое приближение, такое приближение по сути является точным.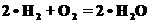 ,
,
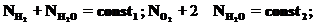 ,
,
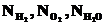 — полное число молекул водорода, кислорода и воды соответственно в данном объеме, который естественно предполагается замкнутым. И возможно кому-то из Вас придётся численно решать задачу типа этой или любую другую задачу, в которой есть какие-то сохраняющиеся величины. В этом случае проверка выполнения законов сохранения может быть использована для контроля точности решения. Больше того, можно (и так часто делают) метод расчета, который автоматически обеспечивает выполнение соответствующих законов сохранения. Возможно, знание этих фактов окажется полезным кому-то из Вас в будущей работе.
— полное число молекул водорода, кислорода и воды соответственно в данном объеме, который естественно предполагается замкнутым. И возможно кому-то из Вас придётся численно решать задачу типа этой или любую другую задачу, в которой есть какие-то сохраняющиеся величины. В этом случае проверка выполнения законов сохранения может быть использована для контроля точности решения. Больше того, можно (и так часто делают) метод расчета, который автоматически обеспечивает выполнение соответствующих законов сохранения. Возможно, знание этих фактов окажется полезным кому-то из Вас в будущей работе.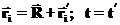 (64)
(64)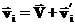 (65)
(65)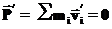
 (67)
(67)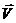 .
.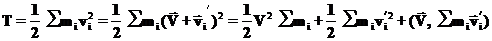 (68)
(68)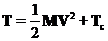 (69)
(69)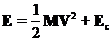 (70)
(70)