
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Связь силы и потенциальной энергии.Потенциальная энергия является очень информативным понятием, поскольку позволяет не только вычислять работу, но и определять силу, которая действует на материальную точку. Покажем, как это можно сделать. Для этого предположим, что частица смещается на малое расстояние вдоль какой-нибудь оси. Для определенности выберем в качестве такой оси, ось X. Запишем работу при перемещении частицы из точки с координатами
Разделив обе части на
Здесь введено обозначение для частной производной. Частная производная это производная по одной из переменных, когда остальные переменные считаются постоянными. Повторяя эту процедуру для каждой из осей можно написать выражение для силы:
Символ
называется градиентом скалярной функции
Однородная сила тяжести:
Упругая сила:
Гравитационные и Кулоновские силы: Запишем потенциальную энергию в общем виде. Имеется в виду, что не будем выбирать систему отсчета, для которой одна из частиц находится в начале координат. Тогда, то согласно (26) и (27) потенциальную энергию можно записать в виде:
и для гравитационных сил 
Поскольку потенциальная энергия зависит только от модуля разности радиус векторов то потенциальную энергию можно дифференцировать как сложную функцию:
Отсюда, получаем для силы, с которой частица 2 действует на частицу 1:
Это выражение мы уже писали раньше, а сейчас поясним, как был продифференцирован модуль разности радиус-векторов:
Эти выкладки поясняют, откуда получилось выражение (37). Согласно проведенным выкладкам сила, с которой частица 1 действует на частицу 2 получается из (37) заменой индексов
Здесь можно заметить, что если потенциальная энергия зависит только от модуля разности радиус-векторов взаимодействующих точек, силы, действующие на частицы равны:
Относительно такой зависимости потенциальной энергии от радиус-векторов взаимодействующих частиц, можно сделать следующие замечания: Силы, к которым приводит потенциал такого вида, автоматически удовлетворяют третьему закону Ньютона (см. (38a) и (38b)). Такой вид потенциала обеспечивает однородность и изотропию пространства. Действительно если нет выделенного направления, то потенциал может зависеть только от модуля расстояния между частицами. Если сдвинуть обе частицы на один и тот же произвольный вектор
Кинетическая энергия Из повседневного опыта мы знаем, что тело массы
Из этого выражения видно что:
Ещё одной особенностью кинетической энергии является то, что произведение массы на квадрат скорости делится на два. Чтобы понять, зачем этот множитель, посмотрим, как изменяется кинетическая энергия под действием некоторой силы
Теперь можно воспользоваться вторым законом Ньютона:
Теперь понятно, почему выражение для кинетической энергии выбирается в таком виде, включая множитель 1/2. Да потому, чтобы скорость изменения этой самой энергии была равна мощности силы (сил), за счет которых она меняется. Теперь мы можем дать ответ на вопрос о том, как изменится кинетическая энергия нашего тела при его перемещении из точки
При переходе к последнему равенству мы воспользовались связью между работой и мощностью (5). Но если сила, которая действует на тело, является потенциальной (консервативной) то работу можно посчитать как разность потенциальных энергий (23):
Или, перенося слагаемые в соответствующие части, получаем:
Мы получили закон сохранения механической энергии в поле потенциальных сил, который можно сформулировать следующим образом: «Полная энергия частицы, равная сумме потенциальной и кинетической энергии, остается постоянной величиной». Ну а если у нас на тело действуют несколько сил, то выражение (42) нужно изменить с учетом того, что работа величина аддитивная. Аддитивная означает, что работа нескольких сил равна сумме работ сил действующих на материальную точку. В этом случае изменение кинетической энергии можно записать в виде (сравни с (42)):
Если не все силы, которые, действуют на частицу, являются потенциальными, то закон сохранения энергии можно переписать в виде:
где полная механическая энергия частицы равна:
а Мы получили, что закон сохранения энергии для материальной точки, на которую действуют внешние силы как потенциальные, так не потенциальные можно сформулировать следующим образом: |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 496. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
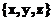 в точку с координатами
в точку с координатами  :
: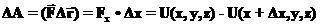
 и устремив
и устремив  получим:
получим:
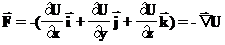
 называется набла, а вектор
называется набла, а вектор 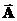 , который получается из скалярной функции
, который получается из скалярной функции  согласно правилу:
согласно правилу:

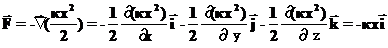

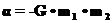 , а для Кулоновских
, а для Кулоновских  и мы учли, что в формулах (26) и (27)
и мы учли, что в формулах (26) и (27)  означает вектор, проведенный от одной частицы к другой. Из этого выражения видно, что потенциальная энергия зависит только от модуля разности радиус-векторов взаимодействующих частиц. При этом сила, которая действует на соответствующую частицу, равна:
означает вектор, проведенный от одной частицы к другой. Из этого выражения видно, что потенциальная энергия зависит только от модуля разности радиус-векторов взаимодействующих частиц. При этом сила, которая действует на соответствующую частицу, равна:

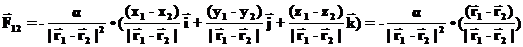
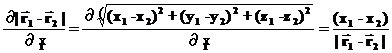
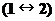 :
:

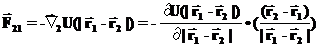
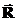 , то при таком преобразовании (оно записывается в виде
, то при таком преобразовании (оно записывается в виде  ) относительное расстояние между частицами не меняется
) относительное расстояние между частицами не меняется  , а значит и не меняется величина потенциальной энергии. Т.е. Потенциальная энергия будет одинаковой где бы не находилась частица 1, если частица 2 находится на одном и том же расстоянии от неё.
, а значит и не меняется величина потенциальной энергии. Т.е. Потенциальная энергия будет одинаковой где бы не находилась частица 1, если частица 2 находится на одном и том же расстоянии от неё. может совершить работу, если столкнется с препятствием, или, говоря другим языком, попадет в поле некоторых сил, гасящих его скорость.Спрашивается можно ли найти характеристику тела, которая характеризует способность тела совершать работу.Из школьного курса известно, что такой характеристикой является кинетическая энергия. Прежде чем напомнить определение кинетической энергии заметим, что мы не ставим вопрос о том какую работу может совершить тело за счет других источников (например, взрывчатки, бензина в баке столкнувшегося с препятствием автомобиля и т.п.). Поэтому будем считать наше тело материальной точкой. Для материальной точки массы
может совершить работу, если столкнется с препятствием, или, говоря другим языком, попадет в поле некоторых сил, гасящих его скорость.Спрашивается можно ли найти характеристику тела, которая характеризует способность тела совершать работу.Из школьного курса известно, что такой характеристикой является кинетическая энергия. Прежде чем напомнить определение кинетической энергии заметим, что мы не ставим вопрос о том какую работу может совершить тело за счет других источников (например, взрывчатки, бензина в баке столкнувшегося с препятствием автомобиля и т.п.). Поэтому будем считать наше тело материальной точкой. Для материальной точки массы  , кинетическая энергия по определению равна:
, кинетическая энергия по определению равна:

 .
.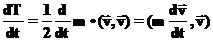

 в точку
в точку  . Заметьте, мы не спрашиваем, какие координаты будет иметь наше тело, мы только интересуемся, как изменится кинетическая энергия при переходе из одной точки в другую. Бывают случаи, когда мы точно знаем, что тело в какой-то момент времени в данной точке окажется. Самый простой, это санки, которые когда-то доедут до конца горки. Итак, изменение кинетической энергии равно (вспоминаем формулу Ньютона-Лейбница):
. Заметьте, мы не спрашиваем, какие координаты будет иметь наше тело, мы только интересуемся, как изменится кинетическая энергия при переходе из одной точки в другую. Бывают случаи, когда мы точно знаем, что тело в какой-то момент времени в данной точке окажется. Самый простой, это санки, которые когда-то доедут до конца горки. Итак, изменение кинетической энергии равно (вспоминаем формулу Ньютона-Лейбница):



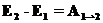 ,
,
 ,
,
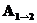 — работа неконсервативных сил.
— работа неконсервативных сил.