Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Работа сил тяготения и Кулоновских сил.Стр 1 из 3Следующая ⇒ Работа и мощность. Закон сохранения энергии Закон всемирного тяготения. Упругие силы. Силы трения. Понятие механической работы и мощности. Потенциальная энергия. Консервативные силы. Энергия упругой деформации. Закон сохранения энергии. Упругие и неупругие столкновения тел. Работа и мощность. Такие понятия как энергия, мощность работа встречались ещё в школьном курсе физики и встречаются в жизни (особенно часто понятие мощности). Напомним некоторые определения. Работа характеризует действие силы на материальную точку. Как всегда в физике бывают интегральные характеристики и дифференциальные. Элементарной работой силы
Относительно этого определения можно сделать следующие пояснения:
Суммарную (интегральную) работу силы на некотором участке можно записать в виде
В СИ единица измерения работы называется Джоулем и равна::
Наряду с работой используют также величину, которая показывает скорость измерения работы и называется мощностью:
В системе СИ мощность измеряется ваттах (Вт) (1 Вт = 1 Дж/с). И согласно (2) суммарная работа, выраженная через мощность равна:
При выполнении каких-то действий с работой или мощностью необходимо иметь в виду о работе (мощности) какой силы идет речь. Если на материальную точку действует несколько сил, то полная работа всех сил равна сумме работ каждой из сил: 
Остановимся на рассмотрении работы совершаемой некоторыми силами, которые были рассматривались раньше.
Работа однородной силы тяжести. Выберем систему координат, в которой ось Z направлена вверх и перпендикулярно поверхности Земли (направлена от центра Земли), а оси X и Y лежат в плоскости Земли. В этом случае на материальную точку массы mдействует постоянная сила:
А элементарная работа равна:
и суммарная работа по перемещению тема (материальной точки) из точки с координатами
Обратим внимание, чтосуммарная работа зависит только от положения начальной и конечной точек и не зависит от того, по какому закону (по какой траектории) двигалась точка.
Работа упругих сил. Выберем систему координат, в которой ось X направлена вдоль пружины (стержня), а оси Y и Z перпендикулярны направлению пружины. Начало координат выберем в положении равновесия. В этом случае на материальную точку массы mдействует упругая сила, которая в выбранной системе координат равна:
При этом для элементарной работы получим:
А суммарная работа дается простым интегралом:
Опять получили, что суммарная работа зависит только от начального и конечного положений. Забавная ситуация получается если мы начиная с какого-то значения
Работа сил тяготения и Кулоновских сил. При рассмотрении работы сил тяготения будем считать, что одна из частиц неподвижна и находится в начале координат, а другая частица движется под действием этой силы. Если обозначить радиус-вектор подвижной частицы через
Отсюда, элементарная работа дается выражением:
Прежде чем подсчитывать суммарную работу приведем равенство, которое позволит просто решить задачу вычисления суммарной работы:
Можно доказать это равенство в векторном виде:
По компонентам это можно пояснить следующими выкладками:
С использованием этого равенства, получаем для суммарной работы в поле гравитационных сил следующее простое выражение:
Опять выходит, что суммарную работу можно найти, зная только начальное и конечное положение материальной точки. Для Кулоновских сил выражение по структуре совпадает с тем, что дает закон всемирного тяготения с заменой масс на заряды, гравитационной постоянной на соответствующий коэффициент:
Знака минус нет, поскольку одноименные заряды отталкиваются. Отсюда понятно, что выражение для Кулоновских сил получается из выражения для работы в поле тяготения (19) с соответствующими заменами констант и знака:
Работа сил трения. В рассмотренных выше случаях работа не зависела от закона движения, а только от начального и конечного положения материальной точки. Возникает вопрос: «а для всех видов сил работу можно вычислить, зная только начальной и конечное положение частицы?» Ответ на этот вопрос отрицательный. Чтобы показать это, достаточно рассмотреть хотя бы один пример, когда это не так. Т.е. когда тело приходит из одной точки в другую по двум разным траекториям и совершает разную работу. Для этого рассмотрим перемещение тела из точки (1) в точку (2) по двум разным траекториям (Рис.1). Рис.1
Здесь Мы пришли к выводу, что существуют два типа сил.
Работу сил по замкнутой траектории можно записать как интеграл по контуру. Для консервативных сил этот интеграл равен нулю, а для неконсервативных — нет. Таким образом, условие потенциальности сил записывается в виде
Мы показали, что консервативными силами являются: 1. Однородные силы 2. Гравитационные силы 3. Кулоновские силы 4. Упругие силы Примерами неконсервативных сил являются: 1. Сила трения 2. Сила сопротивления Случай с силой сопротивления (
Потенциальная энергия. Поскольку для потенциальных сил величина работы зависит только от начального и конечного положений, то можно ввести такую функцию, которая позволяет рассчитывать работу, не вычисляя сложных интегралов. Разность значений этой функции в начальной и конечной точках будет давать нам величину работы совершенной этими силами:
Из этой формулы видно, что потенциальная энергия определяется с точностью до произвольной постоянной (константы), которая не влияет на величину разности в (23). Из рассмотренных выше примеров можно написать выражение для потенциальной энергии в случае рассмотренных выше потенциальных сил:
И начало отсчета выбирается в положении равновесия.
Константы мы всегда будем выбирать равными нулю. Они не влияют на величину работы т.к. взаимно уничтожаются при вычитании. Однако их нужно выбрать раз и навсегда. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 346. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется скалярное произведение этой силы на бесконечно малое перемещение:
называется скалярное произведение этой силы на бесконечно малое перемещение:
 )
)






 в точку с координатами
в точку с координатами  оказывается равной:
оказывается равной:



 сжали (или растянули) пружину а потом вернулись в прежнее положение
сжали (или растянули) пружину а потом вернулись в прежнее положение 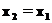 . Тогда получается (см. (12)), что мы совершили нулевую работу. Это правильный ответ, поскольку на одном участке мы сжимали пружину, и работа упругой силы была отрицательной, а когда пружина распрямлялась из сжатого положения, то те же силы совершили точно такую же положительную работу.
. Тогда получается (см. (12)), что мы совершили нулевую работу. Это правильный ответ, поскольку на одном участке мы сжимали пружину, и работа упругой силы была отрицательной, а когда пружина распрямлялась из сжатого положения, то те же силы совершили точно такую же положительную работу. , то гравитационная сила, которая на неё действует равна:
, то гравитационная сила, которая на неё действует равна:


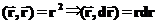



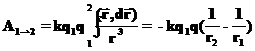

 , то выражение для соответствующих работ равно:
, то выражение для соответствующих работ равно:
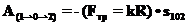
 и
и  пути пройденные частицей при перемещении по траектории (1-2) и (1-0-2) соответственно. Из рисунка видно, что пути для рассмотренных траекторий не совпадают, и силы трения совершают разную работу, хотя обе траектории начинаются и заканчиваются в одной и той же точке.
пути пройденные частицей при перемещении по траектории (1-2) и (1-0-2) соответственно. Из рисунка видно, что пути для рассмотренных траекторий не совпадают, и силы трения совершают разную работу, хотя обе траектории начинаются и заканчиваются в одной и той же точке.

 ) не рассматривался, но очевидно, что эта сила неконсервативная. Достаточно, например, рассмотреть случай, когда частица с постоянной по модулю скоростью
) не рассматривался, но очевидно, что эта сила неконсервативная. Достаточно, например, рассмотреть случай, когда частица с постоянной по модулю скоростью  описывает окружность радиуса
описывает окружность радиуса  и возвращается в прежнее положение. Очевидно, что в этом случае:
и возвращается в прежнее положение. Очевидно, что в этом случае: