
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Твердые тела. Моно- и поликристаллы⇐ ПредыдущаяСтр 20 из 20 Твердые тела (кристаллы) характеризуются наличием значительных сил межмолекулярного взаимодействия и сохраняют постоянными не только свой объем, но и форму. Кристаллы имеют правильную геометрическую форму, которая, как показали рентгенографические исследования немецкого физика-теоретика М. Лауэ (1879—1960), является результатом упорядоченного расположения частиц (атомов, молекул, ионов), составляющих кристалл. Структура, для которой характерно регулярное расположение частиц с периодической повторяемостью в трех измерениях, называется кристаллической решеткой. Точки, в которых расположены частицы, а точнее — средние равновесные положения, около которых частицы совершают колебания, называются узлами кристаллической решетки. Кристаллические тела можно разделить на две группы: монокристаллы и поликристаллы. Монокристаллы — твердые тела, частицы которых образуют единую кристаллическую решетку. Кристаллическая структура монокристаллов обнаруживается по их внешней форме. Хотя внешняя форма монокристаллов одного типа может быть различной, но углы между соответствующими гранями у них остаются постоянными. Это закон постоянства углов, сформулированный М. В. Ломоносовым. Он сделал важный вывод, что правильная форма кристаллов связана с закономерным размещением частиц, образующих кристалл. Монокристаллами являются большинство минералов. Однако крупные природные монокристаллы встречаются довольно редко (например, лед, поваренная соль, исландский шпат). В настоящее время многие монокристаллы выращиваются искусственно. Условия роста крупных монокристаллов (чистый раствор, медленное охлаждение и т. д.) часто не выдерживаются, поэтому большинство твердых тел имеет мелкокристаллическую структуру, т. е. состоит из множества беспорядочно ориентированных мелких кристаллических зерен. Такие твердые тела называются поликристаллами (многие горные породы, металлы и сплавы).  Характерной особенностью монокристаллов является их анизотропность, т. е. зависимость физических свойств — упругих, механических, тепловых, электрических, магнитных, оптических — от направления. Анизотропия монокристаллов объясняется тем, что в кристаллической решетке различно число частиц, приходящихся на одинаковые по длине, но разные по направлению отрезки (рис. 102), т. е. плотность расположения частиц кристаллической решетки по разным направлениям неодинакова, что и приводит к различию свойств кристалла вдоль этих направлений. В поликристаллах анизотропия наблюдается только для отдельных мелких кристалликов, но их различная ориентация приводит к тому, что свойства поликристалла по всем направлениям в среднем одинаковы.
31.
§ 31. Типы кристаллических твердых тел Существует два признака для классификации кристаллов: 1) кристаллографический; 2) физический (природа частиц, расположенных в узлах кристаллической решетки, и характер сил взаимодействия между ними). 1. Кристаллографический признак кристаллов. В данном случае важна только пространственная периодичность в расположении частиц, поэтому можно отвлечься от их внутренней структуры, рассматривая частицы как геометрические точки. Кристаллическая решетка может обладать различными видами симметрии. Симметрия кристаллической решетки — ее свойство совмещаться с собой при некоторых пространственных перемещениях, например параллельных переносах, поворотах, отражениях или их комбинациях и т. д. Кристаллической решетке, как доказал русский кристаллограф Е. С. Федоров (1853—1919), присущи 230 комбинаций элементов симметрии, или 230 различных пространственных групп. С переносной симметрией в трехмерном пространстве связывают понятие трехмерной периодической структуры — пространственной решетки, или решетки Бравэ, представление о которой введено французским кристаллографом О. Бравэ (1811—1863). Всякая пространственная решетка может быть составлена повторением в трех различных направлениях одного и того же структурного элемента — элементарной ячейки. Всего существует 14 типов решеток Бравэ, различающихся по виду переносной симметрии. Они распределяются по семи кристаллографическим системам, или сингониям, представленным в порядке возрастающей симметрии в табл. 3. Для описания элементарных ячеек пользуются кристаллографическими осями координат, которые проводят параллельно ребрам элементарной ячейки, а начало координат выбирают в левом углу передней грани элементарной ячейки. Элементарная кристаллическая ячейка представляет собой параллелепипед, построенный на ребрах а, b, сс углами a, b и g между ребрами (табл. 3). Величины а, bи с и a, b и g называются параметрами элементарной ячейки и однозначно ее определяют. 2. Физический признак кристаллов. В зависимости от рода частиц, расположенных в узлах кристаллической решетки, и характера сил взаимодействия между ними кристаллы разделяются на четыре типа: ионные, атомные, металлические, молекулярные. Ионные кристаллы. В узлах кристаллической решетки располагаются поочередно ионы противоположного знака. Типичными ионными кристаллами являются большинство галоидных соединений щелочных металлов (NaCl, CsCl, КВr и т. д.), а также оксидов различных элементов (MgO, СаО и т. д.). Структуры решеток двух наиболее характерных ионных кристаллов — NaCl (решетка представляет собой две одинаковые гранецентрированные кубические решетки, вложенные друг в друга; в узлах одной из этих решеток находятся ионы Na+, в узлах другой — ионы Cl–) и CsCl (кубическая объемно центрированная решетка — в центре каждой элементарной решетки находится ион) — показаны на рис. 103. Силы взаимодействия между ионами являются в основном электростатическими (кулоновскими).Связь, обусловленная кулоновскими силами притяжения между разноименно заряженными ионами, называетсяионной (илигетерополярной).В ионной решетке нельзя выделить отдельные молекулы: кристалл представляет собойкак бы одну гигантскую молекулу.
Таблица 3
Атомные кристаллы. В узлах кристаллической решетки располагаются нейтральные атомы, удерживающиеся в узлах решеткигомеополярными, или ковалентными, связями квантово-механического происхождения (у соседних атомов обобществлены валентные электроны, наименее связанные с атомом). Атомными кристаллами являются алмаз и графит (два различных состояния углерода), некоторые неорганические соединения (ZnS, ВеО и т. д.), а также типичные полупроводники — германий Ge и кремний Si. Структура решетки алмаза приведена на рис. 104, где каждый атом углерода окружен четырьмя такими же атомами, которые располагаются на одинаковых расстояниях от него в вершинах тетраэдров. Валентные связи осуществляются парами электронов, движущихся по орбитам, охватывающим оба атома, и носят направленный характер: ковалентные силы направлены от центрального атома к вершинам тетраэдра. В отличие от графита решетка алмаза не содержит плоских слоев, что не позволяет сдвигать отдельные участки кристалла, поэтому алмаз является прочным соединением.
Молекулярные кристаллы. В узлах кристаллической решетки располагаются нейтральные молекулы вещества, силы взаимодействия между которыми обусловлены незначительным взаимным смещением электронов в электронных оболочках атомов. Эта силы называются ван-дер-ваальсовыми, так как они имеют ту же природу, что и силы притяжения между молекулами, приводящими к отклонению газов от идеальности. Молекулярными кристаллами являются, например, большинство органических соединений (парафин, спирт, резина и т. д.), инертные газы (Ne, Аr, Кr, Хе) и газы СО2, О2, N2 в твердом состоянии, лед, а также кристаллы брома Вr2, иодаI2. Ван-дер-ваальсовы силы довольно слабые, поэтому молекулярные кристаллы легко деформируются. В некоторых твердых телах одновременно может осуществляться несколько видов связи. Примером может служить графит (гексагональная решетка). Решетка графита (рис. 105) состоит из ряда параллельных плоскостей, в которых атомы углерода расположены в вершинах правильных шестиугольников. Расстояние между плоскостями более чем в два раза превышает расстояние между атомами шестиугольника. Плоские слои связаны друг с другом ван-дер-ваальсовыми силами. В пределах слоя три валентных электрона каждого атома углерода образуют ковалентную связь с соседними атомами углерода, а четвертый электрон, оставаясь «свободным», коллективизируется, но не во всей решетке, как в случае металлов, а в пределах одного слоя. Таким образом, в данном случае осуществляются три вида связи: гомеополярная и металлическая — в пределах одного слоя; ван-дер-ваальсова — между слоями. Этим объясняется мягкость графита, так как его слон могут скользить друг относительно друга. Различие в строении кристаллических решеток двух разновидностей углерода — графита и алмаза — объясняет различие в их физических свойствах: мягкость графита и твердость алмаза; графит — проводник электричества, алмаз — диэлектрик (нет свободных электронов) и т. д.
Расположение атомов в кристаллах характеризуется такжекоординационным числом — числом ближайших однотипных с данным атомом соседних атомов в кристаллической решетке или молекул в молекулярных кристаллах. Для модельного изображения кристаллических структур из атомов и ионов пользуются системой плотной упаковки шаров. Рассматривая простейший случай плотной упаковки шаров одинакового радиуса на плоскости, приходим к двум способам их расположения (рис. 106, а, б). Правая упаковка является более плотной, так как при равном числе шаров площадь ромба со стороной, равной стороне квадрата, меньше площади квадрата. Как видно из рисунка, различие в упаковках сводится к различию координационных чисел: в левой упаковке координационное число равно 4, в правой — 6, т. е. чем плотнее упаковка, тем больше координационное число. Рассмотрим, при каких условиях плотная упаковка шаров в пространстве может соответствовать той или иной кристаллической структуре, приводимой ранее. Начнем строить решетку со слоя шаров, представленных на рис. 106, б. Для упрощения дальнейших рассуждений спроецируем центры шаров на плоскость, на которой они лежат, обозначив их белыми кружками (рис. 107). На эту же плоскость спроецируем центры просветов между шарами, которые обозначены на рис. 107 соответственно черными кружками и крестиками. Любой плотноупакованный слой будем называть слоем А, если центры его шаров расположены над серыми кружками, слоем В — если над красными кружками, слоем С — если над крестиками. Над слоем А уложим второй плотноупакованный слой так, чтобы каждый шар этого слоя лежал на трех шарах первого слоя. Это можно сделать двояко: взять в качестве второго слоя либо В, либо С. Третий слой можно опять уложить двояко и т. д. Итак, плотную упаковку можно описать как последовательность АВСВАС..., в которой не могут стоять рядом слои, обозначенные одинаковыми буквами. Из множества возможных комбинаций в кристаллографии реальное значение имеют два типа упаковки: 1) двухслойная упаковка АВАВАВ... — гексагональная плотноупакованная структура (рис. 108); 2) трехслойная упаковка АВСАВС... — кубическая гранецентрированная структура (рис. 109). В обеих решетках координационное число равно 12 и плотность упаковки одинакова — атомы занимают 74% общего объема кристалла. Координационное число, соответствующее кубической объемно центрированной решетке, равно 8, решетке алмаза (см. рис. 104) равно 4. Кроме двух- и трехслойных упаковок можно построить многослойные с большим периодом повторяемости одинаковых слоев, например АВСВАСАВСВАС... — шестислойная упаковка. Существует модификация карбида SiC с периодом повторяемости 6, 15 и 243 слоя. Если кристалл построен из атомов различных элементов, то его можно представить в виде плотной упаковки шаров разных размеров. На рис. 110 приведено модельное изображение кристалла поваренной соли. Крупные ионы хлора (r=181 пм) образуют плотную трехслойную упаковку, у которой большие пустоты заполнены меньшими по размеру ионами натрия (r=98 пм). Каждый ион Na окружен шестью ионами Сl и, наоборот, каждый ион Cl — шестью ионами Na.
§ 32. Дефекты в кристаллах Рассмотренные в § 71 идеальные кристаллические структуры существуют лишь в очень малых объемах реальных кристаллов, в которых всегда имеются отклонения от упорядоченного расположения частиц в узлах решетки, называемые дефектами кристаллической решетки. Дефекты делятся на макроскопические, возникающие в процессе образования и роста кристаллов (например, трещины, поры, инородные макроскопические включения), и микроскопические, обусловленные микроскопическими отклонениями от периодичности. Микродефекты делятся на точечные и линейные. Точечные дефекты бывают трех типов: 1) вакансии — отсутствие атома в узле кристаллической решетки (рис. 111, a); 2) междоузельный атом — атом, внедрившийся в междоузельное пространство (рис. 111, б); 3) примесный атом — атом примеси, либо замещающий атом основного вещества в кристаллической решетке (примесь замещения, рис. 111, в), либо внедрившийся в междоузельное пространство (примесь внедрения, рис. 111, б; только в междоузлии вместо атома основного вещества располагается атом примеси). Точечные дефекты нарушают лишь ближний порядок в кристаллах, не затрагивая дальнего порядка, — в этом состоит их характерная особенность. Линейные дефекты нарушают дальний порядок. Как следует из опытов, механические свойства кристаллов в значительной степени определяются дефектами особого вида — дислокациями. Дислокации — линейные дефекты, нарушающие правильное чередование атомных плоскостей.
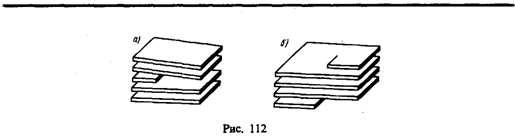
Дислокации бывают краевые и винтовые. Если одна из атомных плоскостей обрывается внутри кристалла, то край этой плоскости образует краевую дислокацию (рис. 112, а). В случае винтовой дислокации (рис. 112, б) ни одна из атомных плоскостей внутри кристалла не обрывается, а сами плоскости лишь приблизительно параллельны и смыкаются друг с другом так, что фактически кристалл состоит из одной атомной плоскости, изогнутой по винтовой поверхности. Плотность дислокаций (число дислокаций, приходящихся на единицу площади поверхности кристалла) для совершенных монокристаллов составляет 102 — 103 см–2, для деформированных кристаллов — 1010 — 1012 см–2. Дислокации никогда не обрываются, они либо выходят на поверхность, либо разветвляются, поэтому в реальном кристалле образуются плоские или пространственные сетки дислокаций. Дислокации и их движение можно наблюдать с помощью электронного микроскопа, а также методом избирательного травления — в местах выхода дислокации на поверхность возникают ямки травления (интенсивное разрушение кристалла под действием реагента), «проявляющие» дислокации. Наличие дефектов в кристаллической структуре влияет на свойства кристаллов, анализ которых проведем ниже. § 33. Теплоемкость твердых тел В качестве модели твердого тела рассмотрим правильно построенную кристаллическую решетку, в узлах которой частицы (атомы, ионы, молекулы), принимаемые за материальные точки, колеблются около своих положений равновесия — узлов решетки — в трех взаимно перпендикулярных направлениях. Таким образом, каждой составляющей кристаллическую решетку частице приписывается три колебательных степени свободы, каждая из которых, согласно закону равнораспределения энергии по степеням свободы (см. § 50), обладает энергиейkT. Внутренняя энергия моля твердого тела
где NA— постоянная Авогадро; NAk=R (R — молярная газовая постоянная). Молярная теплоемкость твердого тела
т. е. молярная (атомная) теплоемкость химически простых тел в кристаллическом
состоянии одинакова (равна 3R) и не зависит от температуры. Этот закон был эмпирически получен французскими учеными П. Дюлонгом (1785—1838) и Л. Пти (1791—1820) и носит названиезакона Дюлонга и Пти. Если твердое тело является химическим соединением (например, NaCl), то число частиц в моле не равно постоянной Авогадро, а равно nNA, где n — число атомов в молекуле (для NaCl число частиц в моле равно 2NA, так, в одном моле NaCl содержится NAатомов Na и NA атомов Cl). Таким образом, молярная теплоемкость твердых химических соединений
т. е. равна сумме атомных теплоемкостей элементов, составляющих это соединение. Как показывают опытные данные (табл. 4), для многих веществ закон Дюлонга и Пти выполняется с довольно хорошим приближением, хотя некоторые вещества (С, Be, В) имеют значительные отклонения от вычисленных теплоемкостей. Кроме того, так же как и в случае газов (см. § 53), опыты по измерению теплоемкости твердых тел при низких температурах показали, что она зависит от температуры (рис. 113). Вблизи нуля кельвин теплоемкость тел пропорциональна Т3, и только при достаточно высоких температурах, характерных для каждого вещества, выполняется условие (73.1). Алмаз, например, имеет теплоемкость, равную 3R при1800 К! Однако для большинства твердых тел комнатная температура является уже достаточно высокой. Таблица 4
Расхождение опытных и теоретических значений теплоемкостей, вычисленных на основе классической теории, объяснили, исходя из квантовой теории теплоемкостей, А. Эйнштейн и П. Дебай. § 34. Испарение, сублимация, плавление и кристаллизация. Аморфные тела Как в жидкостях, так и в твердых телах всегда имеется некоторое число молекул, энергия которых достаточна для преодоления притяжения к другим молекулам и которые способны оторваться от поверхности жидкости или твердого тела и перейти в окружающее их пространство. Этот процесс для жидкости называетсяиспарением(илипарообразованием), для твердых тел —сублимацией (иливозгонкой).
Испарение жидкостей идет при любой температуре, но его интенсивность с повышением температуры возрастает. Наряду с процессом испарения происходит компенсирующий его процесс конденсации пара в жидкость. Если число молекул, покидающих жидкость за единицу времени через единицу поверхности, равно числу молекул, переходящих из пара в жидкость, то наступает динамическое равновесие между процессами испарения и конденсации. Пар, находящийся в равновесии со своей жидкостью, называется насыщенным (см. также § 62). Для большинства твердых тел процесс сублимации при обычных температурах незначителен и давление пара над поверхностью твердого тела мало; оно повышается с повышением температуры. Интенсивно сублимируют такие вещества, как нафталин, камфора, что обнаруживается по резкому, свойственному им запаху. Особенно интенсивно сублимация происходит в вакууме — этим пользуются для изготовления зеркал. Известный пример сублимации — превращение льда в пар — мокрое белье высыхает на морозе. Если твердое тело нагревать, то его внутренняя энергия (складывается из энергии колебаний частиц в узлах решетки и энергии взаимодействия этих частиц) возрастает. При повышении температуры амплитуда колебаний частиц увеличивается до тех пор, пока кристаллическая решетка не разрушится, — твердое тело плавится. На рис. 114, а изображена примерная зависимость Т (Q), где Q — количество теплоты, получаемое телом при плавлении. По мере сообщения твердому телу теплоты его температура повышается, а при температуре плавления Tпл, начинается переход тела из твердого состояния в жидкое. Температура Tпл остается постоянной до тех пор, пока весь кристалл не расплавится, и только тогда температура жидкости вновь начнет повышаться. Нагревание твердого тела до Tпл еще не переводит его в жидкое состояние, поскольку энергия частиц вещества должна быть достаточной для разрушения кристаллической решетки. В процессе плавления теплота, сообщаемая веществу, идет на совершение работы по разрушению кристаллической решетки, а поэтому Tпл = const до расплавления всего кристалла. Затем подводимая теплота пойдет опять-таки на увеличение энергии частиц жидкости и ее температура начнет повышаться. Количество теплоты, необходимое для расплавления 1 кг вещества, называется удельной теплотой плавления.
Если жидкость охлаждать, то процесс протекает в обратном направлении (рис. 114, б; Q' — количество теплоты, отдаваемое телом при кристаллизации): сначала температура жидкости понижается, затем при постоянной температуре, равной Tпл, начинаетсякристаллизация, после ее завершения температура кристалла начнет понижаться. Для кристаллизации вещества необходимо наличие так называемыхцентров кристаллизации — кристаллических зародышей, которыми могут быть не только кристаллики образующегося вещества, но и примеси, а также пыль, сажа и т. д. Отсутствие центров кристаллизации в чистой жидкости затрудняет образование микроскопических кристалликов, и вещество, оставаясь в жидком состоянии, охлаждается до температуры, меньшей температуры кристаллизации, при этом образуется переохлажденная жидкость (на рис. 114, б ей соответствует штриховая кривая). При сильном переохлаждении начинается спонтанное образование центров кристаллизации и вещество кристаллизуется довольно быстро. Обычно переохлаждение расплава происходит от долей до десятков градусов, но для ряда веществ может достигать сотен градусов. Из-за большой вязкости сильно переохлажденные жидкости теряют текучесть, сохраняя, как в твердые тела, свою форму. Эти тела получили название аморфных твердых тел; к ним относятся смолы, мех, сургуч, стекло. Аморфные тела, являясь, таким образом, переохлажденными жидкостями, изотропны, т. е. их свойства во всех направлениях одинаковы; для них, как и для жидкостей, характерен ближний, порядок в расположении частиц; в них в отличие от жидкостей подвижность частиц довольно мала. Особенностью аморфных тел является отсутствие у них определенной точки плавления, т. е. невозможно указать определенную температуру, выше которой можно было бы констатировать жидкое состояние, а ниже — твердое. Из опыта известно, что в аморфных телах со временем может наблюдаться процесс кристаллизации, например в стекле появляются кристаллики; оно, теряя прозрачность, начинает мутнеть и превращаться в поликристаллическое тело. В последнее время широкое распространение в народном хозяйстве получили полимеры — органические аморфные тела, молекулы которых состоят из большого числа одинаковых длинных молекулярных цепочек, соединенных химическими (валентными) связями. К полимерам относятся как естественные (крахмал, белок, каучук, клетчатка и др.), так и искусственные (пластмасса, резина, полистирол, лавсан, капрон и др.) органические вещества. Полимерам присущи прочность и эластичность; некоторые полимеры выдерживают растяжение, в 5—10 раз превышающее их первоначальную длину. Это объясняется тем, что длинные молекулярные цепочки могут при деформации либо сворачиваться в плотные клубки, либо вытягиваться в прямые линии. Эластичность полимеров проявляется только в определенном интервале температур, ниже которого они становятся твердыми и хрупкими, а выше — пластичными. Хотя синтетических полимерных материалов создано очень много (искусственные волокна, заменители кожи, строительные материалы, заменители металлов и др.), но теория полимеров до настоящего времени полностью не разработана. Ее развитие определяется запросами современной техники, требующей синтеза полимеров с заранее заданными свойствами.
§ 35. Фазовые переходы I и П рода Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза — вода; газообразная фаза — смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трехфазной, в которой лед является твердой фазой. Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лед, например, встречается в пяти различных модификациях — фазах). Переход вещества из одной фазы в другую — фазовый переход — всегда связан с качественными изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую). Различают фазовые переходы двух родов. Фазовый переход I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода. Фазовые переходы I рода характеризуются постоянством температуры, изменениями энтропии и объема. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решетки. Подводимая при плавлении теплота идет не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. В подобных переходах — из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние — степень беспорядка увеличивается, т. е., согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет. Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объема, называются фазовыми переходами II рода. Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Общая трактовка фазовых переходов II рода предложена академиком Л. Д. Ландау (1908—1968). Согласно этой трактовке, фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода. Примерами фазовых переходов II рода являются: переход ферромагнитных веществ (железа, никеля) при определенных давлении в температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия (гелия I) при Т=2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести. § 36. Диаграмма состояния. Тройная точка Если система является однокомпонентной, т. е. состоящей из химически однородного вещества или его соединения, то понятие фазы совпадает с понятием агрегатного состояния. Согласно § 60, одно и то же вещество в зависимости от соотношения между удвоенной средней энергией, приходящейся на одну степень свободы хаотического (теплового) движения молекул, и наименьшей потенциальной энергией взаимодействия молекул может находиться в одном из трех агрегатных состояний: твердом, жидком или газообразном. Это соотношение, в свою очередь, определяется внешними условиями — температурой и давлением. Следовательно, фазовые превращения также определяются изменениями температуры и давления. Для наглядного изображения фазовых превращений используется диаграмма состояния (рис. 115), на которой в координатах р,Т задается зависимость между температурой фазового перехода и давлением в виде кривых испарения (КИ), плавления (КП) и сублимации (КС), разделяющих поле диаграммы на три области, соответствующие условиям существования твердой (ТТ), жидкой (Ж) и газообразной (Г) фаз. Кривые на диаграмме называются кривыми фазового равновесия, каждая точка на них соответствует условиям равновесия двух сосуществующих фаз: КП — твердого тела и жидкости, КИ—жидкости и газа, КС—твердого тела и газа. Точка, в которой пересекаются эти кривые и которая, следовательно, определяет условия (температуру Ттр и соответствующее ей равновесное давление ртр) одновременного равновесного сосуществования трех фаз вещества, называется тройной точкой. Каждое вещество имеет только одну тройную точку. Тройная точка воды соответствует температуре 273,16 К (или температуре 0,01°С по шкале Цельсия) и является основной реперной точкой для построения термодинамической температурной шкалы. Термодинамика дает метод расчета кривой равновесия двух фаз одного и того же вещества. Согласно уравнению Клапейрона — Клаузиуса, производная от равновесного давления по температуре равна
где L — теплота фазового перехода, (V2—V1) — изменение объема вещества при переходе его из первой фазы во вторую, Т— температура перехода (процесс изотермический). Уравнение Клапейрона — Клаузиуса позволяет определить наклоны кривых равновесия. Поскольку L и Т положительны, наклон задается знаком V2—V1 . При испарении жидкостей и сублимации твердых тел объем вещества всегда возрастает, поэтому, согласно (76.1), dp/dT>0; следовательно, в этих процессах повышение температуры приводит к увеличению давления, и наоборот. При плавлении большинства веществ объем, как правило, возрастает, т. е. dp/dT>0; следовательно, увеличение давления приводит к повышению температуры плавления (сплошная КП на рис. 115). Для некоторых же веществ (Н2О, Ge, чугун и др.) объем жидкой фазы меньше объема твердой фазы, т. е. dp/dT<0; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая линия на рис. 115).
Диаграмма состояния, строящаяся на основе экспериментальных данных, позволяет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить при том или ином процессе. Например, при условиях, соответствующих точке 1 (рис. 116), вещество находится в твердом состоянии, точке 2 — в газообразном, а точке 3 — одновременно в жидком и газообразном состояниях. Допустим, что вещество в твердом состоянии, соответствующем точке 4, подвергается изобарному нагреванию, изображенному на диаграмме состояния горизонтальной штриховой прямой 4—5—6. Из рисунка видно, что при температуре, соответствующей точке 5, вещество плавится, при более высокой температуре, соответствующей точке 6, — начинает превращаться в газ. Если же вещество находится в твердом состоянии, соответствующем точке 7, то при изобарном нагревании (штриховая прямая 7—8) кристалл превращается в газ минуя жидкую фазу. Если вещество находится в состоянии, соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9—10) оно пройдет следующие три состояния: газ — жидкость — кристаллическое состояние. На диаграмме состояний (см. рис. 115 и 116) видно, что кривая испарения заканчивается в критической точке К. Поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11—12 на рис. 116), т. е. такой переход, который не сопровождается фазовыми превращениями. Это возможно благодаря тому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными). Переход же кристаллического состояния (характеризуется анизотропией) в жидкое или газообразное может быть только скачкообразным (в результате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке. Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где p=0 и T=0 К.
§ 37 Понятие о зонной теории твердых тел Используя уравнение Шредингера — основное уравнение динамики в нерелятивистской квантовой механике, — в принципе можно рассмотреть задачу о кристалле, например найти возможные значения его энергии, а также соответствующие энергетические состояния. Однако как в классической, так и в квантовой механике отсутствуют методы точного решения динамической задачи для системы многих частиц. Поэтому эта задача решается приближенно сведением задачи многих частиц к одноэлектронной задаче об одном электроне, движущемся в заданном внешнем поле. Подобный путь приводит к зонной теории твердого тела. В основе зонной теории лежит так называемое адиабатическоеприближение. Квантово-механическая система разделяется на тяжелые и легкие частицы — ядра и электроны. Поскольку массы и скорости этих частиц значительно различаются, можно считать, что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Принимая, что ядра в узлах кристаллической решетки неподвижны, движение электрона рассматривается в постоянном периодическом поле ядер. Далее используется приближение самосогласованного поля. Взаимодействие данного электрона со всеми другими электронами заменяется действием на него стационарного электрического поля, обладающего периодичностью кристаллической решетки. Это поле создается усредненным в пространстве зарядом всех других электронов и всех ядер. Таким образом, в рамках зонной теории многоэлектронная задача сводится к задаче о движении одного электрона во внешнем периодическом поле — усредненном и согласованном поле всех ядер и электронов. Рассмотрим мысленно «процесс образования» твердого тела из изолированных атомов. Пока атомы изолированы, т. е. находятся друг от друга на макроскопических расстояниях, они имеют совпадающие схемы энергетических уровней (рис. 313). По мере «сжатия» нашей модели до кристаллической решетки, т. е. когда расстояния между атомами станут равными межатомным расстояниям в твердых телах, взаимодействие между атомами приводит к тому, что энергетические уровни атомов смещаются, расщепляются и расширяются в зоны, образуетсязонный энергетический спектр. Из рис. 313, на котором показано расщепление энергетических уровней в зависимости от расстояния r между атомами, видно, что заметно расщепляются и расширяются лишь уровни внешних, валентных электронов, наиболее слабо связанных с ядром и имеющих наибольшую энергию, а также более высокие уровни, которые в основном состоянии атома вообще электронами не заняты. Уровни же внутренних электронов либо совсем не расщепляются, либо расщепляются слабо. Таким образом, в твердых телах внутренние электроны ведут себя так же,как в изолированных атомах, валентные же электроны «коллективизированы» — принадлежат всему твердому телу. Образование зонного энергетического спектра в кристалле является квантово-механическим эффектом в вытекает из соотношения неопределенностей. В кристалле валентные электроны атомов, связанные слабее с ядрами,чем внутренние электроны, могут переходить от атома к атому сквозь потенциальные барьеры, разделяющие атомы, т. е. перемещаться без изменений полной энергии (туннельный эффект, см. § 221). Это приводит к тому, что среднее время жизни t валентного электрона в данном атоме по сравнению с изолированным атомом существенно уменьшается и составляет примерно 10–15 с (для изолированного атома оно примерно 10–8 с). Время же жизни электрона в каком-либо состоянии связано с неопределенностью его энергии (шириной уровня) соотношением неопределенностей DE~h/t (см. (215.5)). Следовательно, если естественная ширина спектральных линий составляет примерно 10–7 эВ, то в кристаллах DE»1¸10 эВ, т. е. энергетические уровни валентных электронов расширяются в зону дозволенных значений энергии. Энергия внешних электронов может принимать значения в пределах закрашенных на рис. 313 областей, называемыхразрешенными энергетическими зонами. Каждая разрешенная зона «вмещает» в себя столько близлежащих дискретных уровней, сколько атомов содержит кристалл: чем больше в кристалле атомов, тем теснее расположены уровни в зоне. Расстояние между соседними энергетическими уровнями в зоне составляет приблизительно 10–22 эВ. Так как оно столь ничтожно, то зоны можно считать практически непрерывными, однако факт конечного числа уровней в зоне играет важную роль для распределения электронов по состояниям. Разрешенные энергетические зоны разделены зонами запрещенных значений энергии, называемымизапрещенными энергетическими зонами. В них электроны находиться не могут. Ширина зон (разрешенных и запрещенных) не зависит от размера кристалла. Разрешенные зоны тем шире, чем слабее связь валентных электронов с ядрами.
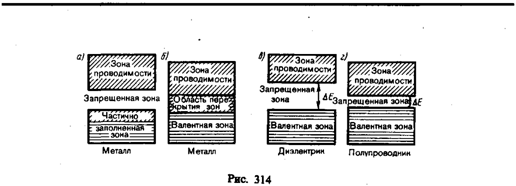
§ 38. Металлы, диэлектрики и полупроводники по зонной теории Зонная теория твердых тел позволила с единой точки зрения истолковать существование металлов, диэлектриков и полупроводников, объясняя различие в их электрических свойствах, во-первых, неодинаковым заполнением электронами разрешенных зон и, во-вторых, шириной запрещенных зон. Степень заполнения электронами энергетических уровней в зоне определяется заполнением соответствующих атомных уровней. Если при этом какой-то энергетический уровень полностью заполнен, то образующаяся энергетическая зона также заполнена целиком. В общем случае можно говорить о валентной зоне, которая полностью заполнена электронами и образована из энергетических уровней внутренних электронов свободных атомов, и о зоне проводимости (свободной зоне), которая либо частично заполнена электронами, либо свободна и образована из энергетических уровней внешних «коллективизированных» электронов изолированных атомов. В зависимости от степени заполнения зон электронами и ширины запрещенной зоны возможны четыре случая, изображенные на рис. 314. На рис. 314, а самая верхняя зона, содержащая электроны, заполнена лишь частично, т. е. в ней имеются вакантные уровни. В данном случае электрон, получив сколь угодно малую энергетическую «добавку» (например, за счет теплового движения или электрического поля), сможет перейти на более высокий энергетический уровень той же зоны, т. е. стать свободным и участвовать в проводимости. Внутризонный переход вполне возможен, так как, например, при 1 К энергия теплового движения kT»10–4 эВ, т. е. гораздо больше разности энергий между соседними уровнями зоны (примерно 10–22 эВ). Таким образом, если в твердом теле имеется зона, лишь частично заполненная электронами, то это тело всегда будет проводником электрического тока. Именно это свойственно металлам. Твердое тело является проводником электрического тока и в том случае, когда валентная зона перекрывается свободной зоной, что в конечном счете приводит к не полностью заполненной зоне (рис. 314, б). Это имеет место для щелочноземельных элементов, образующих II группу таблицы Менделеева (Be, Mg, Ca, Zn, ...). В данном случае образуется так называемая «гибридная» зона, которая заполняется валентными электронами лишь частично. Следовательно, в данном случае металлические свойства щелочноземельных элементов обусловлены перекрытием валентной и свободной зон. Помимо рассмотренного выше перекрытия зон возможно также перераспределение электронов между зонами, возникающими из уровней различных атомов, которое может привести к тому, что вместо двух частично заполненных зон в кристалле окажутся одна полностью заполненная (валентная) зона и одна свободная зона (зона проводимости). Твердые тела, у которых энергетический спектр электронных состояний состоит только из валентной зоны и зоны проводимости, являются диэлектриками или полупроводниками в зависимости от ширины запрещенной зоны DЕ. Если ширина запрещенной зоны кристалла порядка нескольких электрон-вольт, то тепловое движение не может перебросить электроны из валентной зоны в зону проводимости и кристалл является диэлектриком, оставаясь им при всех реальных температурах (рис. 314, в). Если запрещенная зона достаточно узка (DЕ порядка 1 эВ), то переброс электронов из валентной зоны в зону проводимости может быть осуществлен сравнительно легко либо путем теплового возбуждения, либо за счет внешнего источника, способного передать электронам энергию DЕ, и кристалл является полупроводником (рис. 314, г).
Различие между металлами и диэлектриками с точки зрения зонной теории состоит в том, что при 0 К в зоне проводимости металлов имеются электроны, а в зоне проводимости диэлектриков они отсутствуют. Различие же между диэлектриками и полупроводниками определяется шириной запрещенных зон: для диэлектриков она довольно широка (например, для NaClDЕ=6 эВ), для полупроводников — достаточно узка (например, для германия DЕ=0,72 эВ). При температурах, близких к 0 К, полупроводники ведут себя как диэлектрики, так как переброса электронов в зону проводимости не происходит. С повышением температуры у полупроводников растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости, т. е. электрическая проводимость проводников в этом случае увеличивается. § 39 Собственная проводимость полупроводников Полупроводниками являются твердые тела, которые при Т=0 характеризуются полностью занятой электронами валентной зоной, отделенной от зоны проводимости сравнительно узкой (DЕ порядка 1 эВ) запрещенной зоной (рис. 314, г). Своим названием они обязаны тому, что их электропроводность меньше электропроводности металлов и больше электропроводности диэлектриков. В природе полупроводники существуют в виде элементов (элементы IV, V и VI групп Периодической системы элементов Менделеева), например Si, Ge, As, Se, Те, и химических соединений, например оксиды, сульфиды, селениды, сплавы элементов различных групп. Различают собственные и примесные полупроводники. Собственными полупроводниками являются химически чистые полупроводники, а их проводимость называется собственной проводимостью. Примером собственных полупроводников могут служить химически чистые Ge, Se, а также многие химические соединения: InSb, GaAs, CdS и др. При 0 К и отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики. При повышении же температуры электроны с верхних уровней валентной зоны I могут быть переброшены на нижние уровни зоны проводимости II (рис. 315). При наложении на кристалл электрического поля они перемещаются против поля и создают электрический ток. Таким образом, зона II из-за ее частичного «укомплектования» электронами становится зоной проводимости. Проводимость собственных полупроводников, обусловленная электронами, называется электронной проводимостью или проводимостью n-типа (от лат. negative — отрицательный). В результате тепловых забросов электронов из зоны I в зону II в валентной зоне возникают вакантные состояния, получившие названиедырок. Во внешнем электрическом поле на освободившееся от электрона место — дырку — может переместиться электрон с соседнего уровня, а дырка появится в том месте, откуда ушел электрон, и т. д. Такой процесс заполнения дырок электронами равносилен перемещению дырки в направлении, противоположном движению электрона, так, как если бы дырка обладала положительным зарядом, равным по величине заряду электрона. Проводимость собственных полупроводников, обусловленная квазичастицами — дырками, называетсядырочной проводимостью илипроводимостью p-типа (от лат. positive — положительный).
Таким образом, в собственных полупроводниках наблюдаются два механизма проводимости: электронный и дырочный. Число электронов в зоне проводимости равно числу дырок в валентной зоне, так как последние соответствуют электронам, возбужденным в зону проводимости. Следовательно, если концентрации электронов проводимости и дырок обозначить соответственно пe, и nр, то
Проводимость полупроводников всегда являетсявозбужденной, т. е. появляется только под действием внешних факторов (температуры, облучения, сильных электрических полей и т. д.). В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны (рис. 316). Действительно, для переброса электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости затрачиваетсяэнергия активации, равная ширине запрещенной зоны DE. При появлении же электрона в зоне проводимости в валентной зоне обязательно возникает дырка. Следовательно, энергия, затраченная на образование пары носителей тока, должна делиться на две равные части. Так как энергия, соответствующая половине ширины запрещенной зоны, идет на переброс электрона и такая же энергия затрачивается на образование дырки, то начало отсчета для каждого из этих процессов должно находиться в середине запрещенной зоны. Энергия Ферми в собственном полупроводнике представляет собой энергию, от которой происходит возбуждение электронов и дырок. Вывод о расположении уровня Ферми в середине запрещенной зоны собственного полупроводника может быть подтвержден математическими выкладками. В физике твердого тела доказывается, что концентрация электронов в зоне проводимости
где E2—энергия, соответствующая дну зоны проводимости (рис. 316), ЕF — энергия Ферми, Т — термодинамическая температура, С1 — постоянная, зависящая от температуры и эффективной массы электрона проводимости.Эффективная масса — величина, имеющая размерность массы и характеризующая динамические свойства квазичастиц — электронов проводимости и дырок. Введение в зонную теорию эффективной массы электрона проводимости позволяет, с одной стороны, учитывать действие на электроны проводимости не только внешнего поля, но и внутреннего периодического поля кристалла, а с другой стороны, абстрагируясь от взаимодействия электронов проводимости с решеткой, рассматривать их движение во внешнем поле как движение свободных частиц. Концентрация дырок в валентной зоне
где С2 — постоянная, зависящая от температуры и эффективной массы дырки, Е1 — энергия, соответствующая верхней границе валентной зоны. Энергия возбуждения в данном случае отсчитывается вниз от уровня Ферми (рис. 316), поэтому величины в экспоненциальном множителе (242.3) имеют знак, обратный знаку экспоненциального множителя в (242.2). Так как для собственного полупроводника пe=np(242.1), то
Если эффективные массы электронов и дырок равны (
т. е. уровень Ферми в собственном полупроводнике действительно расположен в середине запрещенной зоны. Taк как для собственных полупроводников DE>>kT, то распределение Ферми — Дирака (235.2) переходит в распределение Максвелла — Больцмана. Положив в (236.2) E–EF»DE/2, получим
Количество электронов, переброшенных в зону проводимости, а следовательно, и количество образовавшихся дырок пропорциональны áN(Е)ñ. Таким образом, удельная проводимость собственных полупроводников
где g0 — постоянная, характерная для данного полупроводника. Увеличение проводимости полупроводников с повышением температуры является их характерной особенностью (у металлов с повышением температуры проводимость уменьшается). С точки зрения зонной теории это обстоятельство объяснить довольно просто: с повышением температуры растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости и участвуют в проводимости. Поэтому удельная проводимость собственных полупроводников с повышением температуры растет. Если представить зависимость lng от 1/T, то для собственных полупроводников — это прямая (рис. 317), по наклону которой можно определить ширину запрещенной зоны DЕ, а по ее продолжению — g0 (прямая отсекает на оси ординат отрезок, равный lng0).
Одним из наиболее широко распространенных полупроводниковых элементов является германий, имеющий решетку типа алмаза, в которой каждый атом связан ковалентными связями (см. § 71) с четырьмя ближайшими соседями. Упрощенная плоская схема расположения атомов в кристалле Ge дана на рис. 318, где каждая черточка обозначает связь, осуществляемую одним электроном. В идеальном кристалле при 0 К такая структура представляет собой диэлектрик, так как все валентные электроны участвуют в образовании связей и, следовательно, не участвуют в проводимости. При повышении температуры (или под действием других внешних факторов) тепловые колебания решетки могут привести к разрыву некоторых валентных связей, в результате чего часть электронов отщепляется и они становятся свободными. В покинутом электроном месте возникает дырка (она изображена белым кружком), заполнить которую могут электроны из соседней пары. В результате дырка, так же как и освободившийся электрон, будет двигаться по кристаллу. Движение электронов проводимости и дырок в отсутствие электрического поля является хаотическим. Если же на кристалл наложить электрическое поле, то электроны начнут двигаться против поля, дырки— по полю, что приведет к возникновению собственной проводимости германия, обусловленной как электронами, так и дырками. В полупроводниках наряду с процессом генерации электронов и дырок идет процесс рекомбинации: электроны переходят из зоны проводимости в валентную зону, отдавая энергию решетке и испуская кванты электромагнитного излучения. В результате для каждой температуры устанавливается определенная равновесная концентрация электронов и дырок, изменяющаяся с температурой согласно выражению (242.4).
§ 40. Примесная проводимость полупроводников Проводимость полупроводников, обусловленная примесями, называетсяпримесной проводимостью, а сами полупроводники —примесными полупроводниками. Примесная проводимость обусловлена примесями (атомы посторонних элементов), а также дефектами типа избыточных атомов (по сравнению со стехиометрическим составом), тепловыми (пустые узлы или атомы в междоузлиях) и механическими (трещины, дислокации и т. д.) дефектами. Наличие в полупроводнике примеси существенно изменяет его проводимость. Например, при введении в кремний примерно 0,001 ат.% бора его проводимость увеличивается примерно в 106 раз. Примесную проводимость полупроводников рассмотрим на примере Ge и Si, в которые вводятся атомы с валентностью, отличной от валентности основных атомов на единицу. Например, при замещении атома германия пятивалентным атомом мышьяка (рис. 319, а) один электрон не может образовать ковалентной связи, он оказывается лишним и может быть легко при тепловых колебаниях решетки отщеплен от атома, т. е. стать свободным. Образование свободного электрона не сопровождается нарушением ковалентной связи; следовательно, в отличие от случая, рассмотренного в § 242, дырка не возникает. Избыточный положительный заряд, возникающий вблизи атома примеси, связан с атомом примеси и поэтому перемещаться по решетке не может. С точки зрения зонной теории рассмотренный процесс можно представить следующим образом (рис. 319, б). Введение примеси искажает поле решетки, что приводит к возникновению в запрещенной зоне энергетического уровня D валентных электронов мышьяка, называемогопримеснымуровнем. В случае германия с примесью мышьяка этот уровень располагается от дна зоны проводимости на расстоянии DED=0,013 эВ. Так как DED<kT, то уже при обычных температурах энергия теплового движения достаточна для того, чтобы перебросить электроны примесного уровня в зону проводимости; образующиеся при этом положительные заряды локализуются на неподвижных атомах мышьяка и в проводимости не участвуют. Таким образом, в полупроводниках с примесью, валентность которой на единицу больше валентности основных атомов, носителями тока являются электроны; возникает электронная примесная проводимость (проводимость n-типа). Полупроводники с такой проводимостью называются электронными (или полупроводниками n-типа). Примеси, являющиеся источником электронов, называются донорами, а энергетические уровни этих примесей — донорными уровнями. Предположим, что в решетку кремния введен примесный атом с тремя валентными электронами, например бор (рис. 320, а). Для образования связей с четырьмя ближайшими соседями у атома бора не хватает одного электрона, одна из связей остается неукомплектованной и четвертый электрон может быть захвачен от соседнего атома основного вещества, где соответственно образуется дырка. Последовательное заполнение образующихся дырок электронами эквивалентно движению дырок в полупроводнике, т. е. дырки не остаются локализованными, а перемещаются в решетке кремния как свободные положительные заряды. Избыточный же отрицательный заряд, возникающий вблизи атома примеси, связан с атомом примеси и по решетке перемещаться не может. По зонной теории, введение трехвалентной примеси в решетку кремния приводит к возникновению в запрещенной зоне примесного энергетического уровня А, не занятого электронами. В случае кремния с примесью бора этот уровень располагается выше верхнего края валентной зоны на расстоянии DEA=0,08 эВ (рис. 320, б). Близость этих уровней к валентной зоне приводит к тому, что уже при сравнительно низких температурах электроны из валентной зоны переходят на примесные уровни и, связываясь с атомами бора, теряют способность перемещаться по решетке кремния, т. е. в проводимости не участвуют. Носителями тока являются лишь дырки, возникающие в валентной зоне.
Таким образом, в полупроводниках с примесью, валентность которой на единицу меньше валентности основных атомов, носителями тока являются дырки; возникает дырочная проводимость (проворность p-типа). Полупроводники с такой проводимостью называются дырочными (или полупроводниками p-типа). Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторами, а энергетические уровни этих примесей — акцепторными уровнями. В отличие от собственной проводимости, осуществляющейся одновременно электронами и дырками, примесная проводимость полупроводников обусловлена в основном носителями одного знака: электронами—в случае донорной примеси, дырками — в случае акцепторной. Эти носители тока называются основными. Кроме основных носителей в полупроводнике имеются и неосновные носители: в полупроводниках n-типа — дырки, в полупроводниках p-типа — электроны. Наличие примесных уровней в полупроводниках существенно изменяет положение уровня Ферми ЕF. Расчеты показывают, что в случае полупроводников n-типа уровень Ферми ЕF0 при 0 К расположен посередине между дном зоны проводимости и донорным уровнем (рис. 321), С повышением температуры все большее число электронов переходит из донорных состояний в зону проводимости, но, помимо этого, возрастает и число тепловых флуктуаций, способных возбуждать электроны из валентной зоны и перебрасывать их через запрещенную зону энергий. Поэтому при высоких температурах уровень Ферми имеет тенденцию смещаться вниз (сплошная кривая) к своему предельному положению в центре запрещенной зоны, характерному для собственного полупроводника. Уровень Ферми в полупроводниках р-типа при 0 К ЕF0 располагается посередине между потолком валентной зоны и акцепторным уровнем (рис. 322). Сплошная кривая опять-таки показывает его смещение с температурой. При температурах, при которых примесные атомы оказываются полностью истощенными и увеличение концентрации носителей происходит за счет возбуждения собственных носителей, уровень Ферми располагается посередине запрещенной зоны, как в собственном полупроводнике.
Проводимость примесного полупроводника, как и проводимость любого проводника, определяется концентрацией носителей и их подвижностью. С изменением температуры подвижность носителей меняется по сравнительно слабому степенному закону, а концентрация носителей — по очень сильному экспоненциальному закону, поэтому проводимость примесных полупроводников от температуры определяется в основном температурной зависимостью концентрации носителей тока в нем. На рис. 323 дан примерный график зависимости lng от 1/Tдля примесных полупроводников. Участок AB описывает примесную проводимость полупроводника. Рост примесной проводимости полупроводника с повышением температуры обусловлен в основном ростом концентрации примесных носителей. Участок ВС соответствует области истощения примесей (это подтверждают и эксперименты), участок CD описывает собственную проводимость полупроводника.
§ 41. Фотопроводимость полупроводников Фотопроводимость (см. § 202)полупроводников — увеличение электропроводности полупроводников под действием электромагнитного излучения — может быть связана со свойствами как основного вещества, так и содержащихся в нем примесей. В первом случае при поглощении фотонов, соответствующих собственной полосе поглощения полупроводника, т. е. когда энергия фотонов равна или больше ширины запрещенной зоны (hn³DE), могут совершаться перебросы электронов из валентной зоны в зону проводимости (рис. 324, а), что приведет к появлению добавочных (неравновесных) электронов (в зоне проводимости) и дырок (в валентной зоне). В результате возникает собственная фотопроводимость, обусловленная как электронами, так и дырками. Если полупроводник содержит примеси, то фотопроводимость может возникать и при hn<DE: для полупроводников с донорной примесью фотон должен обладать энергией hn³DЕD, а для полупроводников с акцепторной примесью —hn³DЕA. При поглощении света примесными центрами происходит переход электронов с донорных уровней в зону проводимости в случае полупроводника n-типа (рис. 324, б) или из валентной зоны на акцепторные уровни в случае полупроводника p-типа (рис. 324, в). В результате возникаетпримесная фотопроводимость, являющаяся чисто электронной для полупроводников п-типа и чисто дырочной для полупроводников p-типа.
Таким образом, если
(DEп — в общем случае энергия активации примесных атомов), то в полупроводнике возбуждается фотопроводимость. Из (244.1) можноопределитькрасную границу фотопроводимости — максимальную длину волны, при которой еще фотопроводимость возбуждается: |
||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 1313. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 Металлические кристаллы. В узлах кристаллической решетки располагаются положительные ионы металла. При образовании кристаллической решетки валентные электроны, сравнительно слабо связанные с атомами, отделяются от атомов и коллективизируются: они уже принадлежат не одному атому, как в случае ионной связи, и не паре соседних атомов, как в случае гомеополярной связи, а всему кристаллу в целом. Таким образом, в металлах между положительными ионами хаотически, подобно молекулам газа, движутся «свободные» электроны, наличие которых обеспечивает хорошую электропроводность металлов. Так как металлическая связь не имеет направленного действия и положительные ионы решетки одинаковы по свойствам, то металлы должны иметь симметрию высокого порядка. Действительно, большинство металлов имеют кубическую объемно центрированную (Li, Na, К, Rb, Cs) и кубическую гранецентрированную (Сu, Ag, Pt, Au) решетки. Чаще всего металлы встречаются в виде поликристаллов.
Металлические кристаллы. В узлах кристаллической решетки располагаются положительные ионы металла. При образовании кристаллической решетки валентные электроны, сравнительно слабо связанные с атомами, отделяются от атомов и коллективизируются: они уже принадлежат не одному атому, как в случае ионной связи, и не паре соседних атомов, как в случае гомеополярной связи, а всему кристаллу в целом. Таким образом, в металлах между положительными ионами хаотически, подобно молекулам газа, движутся «свободные» электроны, наличие которых обеспечивает хорошую электропроводность металлов. Так как металлическая связь не имеет направленного действия и положительные ионы решетки одинаковы по свойствам, то металлы должны иметь симметрию высокого порядка. Действительно, большинство металлов имеют кубическую объемно центрированную (Li, Na, К, Rb, Cs) и кубическую гранецентрированную (Сu, Ag, Pt, Au) решетки. Чаще всего металлы встречаются в виде поликристаллов.


 (73.1)
(73.1)




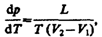 (76.1)
(76.1)



 (242.1)
(242.1)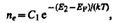 (242.2)
(242.2) (242.3)
(242.3)
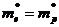 ), то С1=С2 и, следовательно, –(E2–EF)= =E1–EF, откуда
), то С1=С2 и, следовательно, –(E2–EF)= =E1–EF, откуда
 (242.4)
(242.4) (242.5)
(242.5)





 (244.1)
(244.1)