
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Просмотр Углов Ориентации Материала
Можно увидеть углы ориентации материала, которые ранее определены для плоских элементов, используя команду View ⇒ Options. Надо выбрать опцию "Element - Orientation/Shape", и включить режим "Show Orientation". Эта команда покажет маленький вектор в центре каждого элемента, для которого угол был определен. Ориентация вектора показывает выбранный угол. Обычно просто надо убедиться, что все векторы параллельны – значит, элементы выравнены.
Приложение 2. Краткие сведения о теориях разрушения ортотропных материалов
Индексы разрушения
В анализе изотропных материалов прочность не зависит от ориентации материала под нагрузкой и в нем можно сравнивать вычисленные наибольшие главные напряжения с допустимыми напряжениями, обеспечивающими целостность структуры. Напротив, слоистые композиты являются ортотропными материалами и могут проявлять разные свойства при растяжении и сжатии. Таким образом, прочность этих ортотропных слоев является функцией ориентации материала относительно действующих напряжений. Целостность структуры будет зависеть от определения допустимого поля напряжений. Основная составная часть этого определения – введение набора допустимых напряжений или сил в главных направлениях материала. Введем обозначения Xt = Допустимое растягивающее напряжение в главном направлении x (или 1) материала. Xc = Допустимое сжимающее напряжение в главном направлении х (или 1) материала. Yt = Допустимое растягивающее напряжение в главном направлении y (или 2) материала. Yc = Допустимое сжимающее напряжение в главном направлении у (или 2) материала.  S = Допустимое напряжение сдвига в главной системе материала.
Выражения для доступных в NASTRAN’е теорий разрушения показаны в таблице 1.
Таблица 1. Теории разрушения поддерживаемые в MSC/NASTRAN
Теория Хилла (Failure Theory ID = “HILL”)
где X ‑ допустимое напряжение в направлении 1 Y ‑ допустимое напряжение в направлении 2 S – допустимое напряжение сдвига и Обратите внимание на то, что теория Хилла используется для материалов, которые имеют одинаковую прочность на растяжение и сжатие. График вышеприведенного уравнения, полученный установкой индекса разрушения в 1 на плоскости
Теория Хоффмана (Failure Theory ID = “HOFF”)
Теория Хоффмана для ортотропного слоя в общем состоянии плоского напряжения задается выражением:
Индекс разрушения получается вычислением левой части приведенного выше уравнения. Обратите внимание, что эта теория принимает в учет разницу между допустимыми напряжениями растяжения и сжатия, используя линейные члены в уравнении.
Тензорная полиномиальная теория Цая-Вю (Failure Theory ID = “TSAI”)
Теория прочности для анизотропных материалов, предложенная Цаем и Вю, специализированная для случая ортотропного слоя в общем состоянии плоского напряжения:
где
и Величина
Необходимость удовлетворения критерия стабильности, вместе с необходимым условием экспериментального определения Индекс разрушения материала связующего будет вычислен как максимальное напряжение межслоевого сдвига, поделенное на допустимое напряжение связующего. Индексы разрушения для всех слоев будут записаны в OEFIT (Output Element Failure Index Table – Выходная таблица индексов разрушения элементов), которая будет выведена, если запросить вывод напряжений. Индекс разрушения элемента есть наибольшая величина индексов разрушения для всех слоев элемента.
Теория максимальных деформаций (Failure Theory ID = “STRN”)
Деформации и искривления средней плоскости выдаются NASTRAN’ом в системе координат элемента. Из них напряжение и деформации в каждом отдельном слое в направлении волокон и поперечном направлении могут быть вычислены довольно легко. Чтобы запросить вывод деформаций слоев используется PARAM,LSTRN,1.0. Критерий максимальных деформаций не имеет членов взаимодействия. Допустимые деформации, указываемые в статье MAT8 для каждого слоя, включают:
Индекс разрушения вычисляется, используя
и
Т.е. индекс разрушения:
Дополнительно пользователь должен быть проинформирован, который вид индекса разрушения критичен, т.е. продольный (1), поперечный (2), или сдвига (3). Таким образом, в выводе индексов разрушения мнемоники 1, 2, 12 напечатаны как значения FP, чтобы показать критическое направление. Способ расчета индекса разрушения для межслоевых напряжений сдвига не изменяется. Вполне возможно, что для теории максимальных деформаций пользователь может пожелать указать в статье MAT8 допустимое напряжение слоя вместо допустимой деформации. Это можно сделать, оставляя в MAT8 пустым поле STRN. Для этого случая индексы разрушения вычисляются, используя
и
т.е. индекс разрушения:
Напряжения и деформации межслоевого сдвига
Классическая слоистая теория, которая использует предположение о плоских напряжениях, не учитывает межслоевой сдвиг. В результате эта теория не может быть использована для предсказания величины этих напряжений. Высокие значения этих межслоевых напряжений могут привести к разрушению, которое характерно только для композиционных материалов. Для вычисления межслоевых напряжений сдвига используется приближенная техника. Основное предположение этой приближенной техники заключается в том, что х- и у-компоненты напряжений не зависят одно от другого. Это допущение позволяет вывести желаемый результат из рассмотрения балки с поперечным сечением единичной ширины. Межслоевые деформации сдвига вычисляются путем
Приложение 3. Примеры решения задач
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 299. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
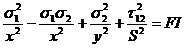
 и
и  .
.

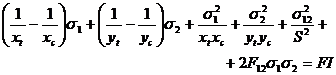

 (1)
(1) , если
, если 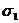 положительно, или
положительно, или 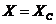 , если
, если 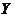 и
и  . Для члена взаимодействия
. Для члена взаимодействия  ,
,  положительно, или
положительно, или  , если
, если  дает эллипс и является анизотропным критерием текучести Хилла (позднее модифицированный Цаем и, с тех пор, иногда называемый теорией Цая-Хилла). Следовательно, если индекс разрушения, вычисленный таким образом, меньше 1, напряжения слоя находятся внутри эллипса текучести и слой называется “безопасным”; напротив, если индекс разрушения больше 1, напряжения слоя находятся вне эллипса текучести и слой поврежден.
дает эллипс и является анизотропным критерием текучести Хилла (позднее модифицированный Цаем и, с тех пор, иногда называемый теорией Цая-Хилла). Следовательно, если индекс разрушения, вычисленный таким образом, меньше 1, напряжения слоя находятся внутри эллипса текучести и слой называется “безопасным”; напротив, если индекс разрушения больше 1, напряжения слоя находятся вне эллипса текучести и слой поврежден. (2)
(2) (3)
(3)
 определяется экспериментально.
определяется экспериментально. (4)
(4) является предпочтительной альтернативой экспериментальному определению
является предпочтительной альтернативой экспериментальному определению  ‑ Допустимые деформации растяжения и сжатия, соответственно, в продольном направлении.
‑ Допустимые деформации растяжения и сжатия, соответственно, в продольном направлении.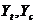 ‑ Допустимые деформации растяжения и сжатия, соответственно, в поперечном направлении.
‑ Допустимые деформации растяжения и сжатия, соответственно, в поперечном направлении. ‑ Допустимые деформации сдвига в плоскости.
‑ Допустимые деформации сдвига в плоскости.
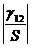
 .
.

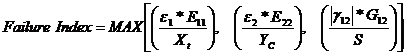
 и
и 