
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПОРЯДОК РАСЧЕТА УСТАНОВИВШЕГОСЯ СЛУЧАЙНОГО ПРОЦЕССА В СИСТЕМЕ УПРАВЛЕНИЯСтр 1 из 3Следующая ⇒ Им. Д. Ф. УСТИНОВА
КУРСОВая работа по учебной дисциплине Спецглавы теории автоматического управления
на тему Параметрический синтез нелинейной стохастической системы
студентки _____________Цыкиной Юлии Николаевны__________ Фамилия , Имя , Отчество студента
группы ______И361________
САНКТ-ПЕТЕРБУРГ 2009 г. СОДЕРЖАНИЕ
ВВЕДЕНИЕ
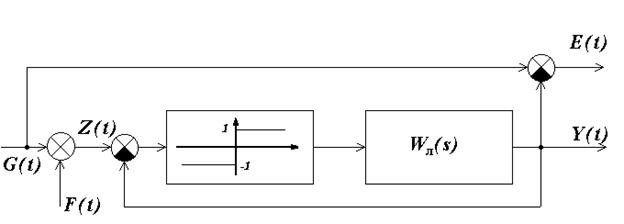
Задана структурная схема системы (рисунок 1)
Рисунок 1.
и передаточная функция детерминированной части:
Задающее воздействие детерминированное: Помеха
Требуется: 1. Рассчитать зависимости математического ожидания и дисперсии ошибки системы 2. Выбрать оптимальное значение  Исходные данные представлены в таблице.
ПОРЯДОК РАСЧЕТА УСТАНОВИВШЕГОСЯ СЛУЧАЙНОГО ПРОЦЕССА В СИСТЕМЕ УПРАВЛЕНИЯ
Для расчета установившегося случайного процесса в системе при стационарных случайных воздействиях применяется спектральный метод. Данный аналитический метод, называемый также методом передаточных функций, детально развит в рамках теории автоматического управления [1,2] и основан на использовании структурно-динамических схем систем и спектральных плотностей случайных процессов. Непосредственное использование спектральных плотностей возможно только для стационарных процессов. Поэтому данный метод позволяет строить модели процессов, соответствующих некоторым установившимся режимам в стационарных системах при стационарных воздействиях. Применение данного метода основано на использовании двух свойств линейных систем: 1. Реакция линейной системы на совокупность входных воздействий может быть определена как сумма ее реакций на каждое из них в отдельности (принцип суперпозиции). 2. Случайный сигнал на выходе физически реализуемого линейного динамического звена имеет закон распределения, близкий к нормальному (свойство фильтра). Второе свойство, строго говоря, имеет место при следующем соотношении между порядком знаменателя n и числителя m передаточной функции звена или системы: n – m ≥ 2. Однако его обычно используют во всех случаях, когда выполняется условие физической реализуемости n–m ≥ 1. Благодаря указанным свойствам оказывается возможным изолированно рассматривать преобразование линейной системой детерминированных и центрированных случайных составляющих входных сигналов и ограничиваться для выходного сигнала или ошибки системы нахождением только математического ожидания и дисперсии, полностью определяющих нормальный закон распределения. Для оценки корреляционных свойств выходных сигналов используются корреляционные функции и спектральные плотности. Каждый случайный входной сигнал преобразуется в сумму:
где mg(t) - детерминированная составляющая, или математическое ожидание входного сигнала; Модель преобразования детерминированной составляющей строится на основе стандартного аппарата передаточных функций:
L[my(t)] = Φ(p)L[mg(t)], где L[mg(t)], L[my(t)] - изображения по Лапласу детерминированных составляющих соответственно входного и выходного сигналов; Φ(p) - передаточная функция звена или системы. Выходной сигнал в установившемся процессе может быть определен по теореме о конечном значении:
Например, при mg(t)=const для асимптотически устойчивой системы получим: my=Φ(0)mg=const. Модель преобразования центрированной случайной составляющей строится для спектральных плотностей Sy(ω)=|Φ(jω)|2Sg(ω), где спектральная плотность входного сигнала определяется по его корреляционной функции
По полученной спектральной плотности выходного сигнала находят его дисперсию:
Этот интеграл обычно удается привести к форме:
где hn(jω)=b1(jω)2n-2 +b2(jω)2n-4 +...+bn, gn(jω)=a0(jω)n +a1(jω)n-1 +...+an. (1) Тогда:
где ∆n - n-й определитель Гурвица для многочлена gn(p) [3], а ∆'n получается из ∆nзаменой 1-й строки коэффициентами многочлена hn. Например, при n=4
Для системы с несколькими случайными входными сигналами, если они не коррелированы между собой, математическое ожидание и дисперсия выходного сигнала определяются на основе принципа суперпозиции:
где Таким образом, выходной сигнал определяется в форме Аналогичный подход используется при нахождении ошибки системы. Она определяется в форме: Тогда математическое ожидание ошибки определяется в виде суммы:
где Дисперсия ошибки совпадает с дисперсией выходного сигнала. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 203. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 .
.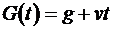 .
.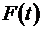 - стационарная случайная функция с математическим ожиданием, равным нулю, и спектральной плотностью
- стационарная случайная функция с математическим ожиданием, равным нулю, и спектральной плотностью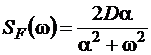 .
. от величины коэффициента передачи
от величины коэффициента передачи  в установившемся процессе. Автоколебания в системе считаются недопустимыми .
в установившемся процессе. Автоколебания в системе считаются недопустимыми .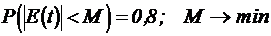 .
.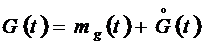 ,
, - центрированная случайная составляющая входного сигнала (случайный процесс с нулевым математическим ожиданием).
- центрированная случайная составляющая входного сигнала (случайный процесс с нулевым математическим ожиданием).


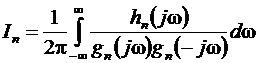 ,
, , (2)
, (2)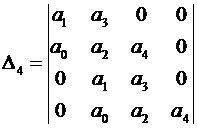 ,
,  . (3)
. (3)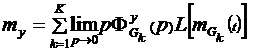 ,
, ,
, и
и  - математическое ожидание и спектральная плотность k-го входного сигнала (задающего или возмущающего воздействия);
- математическое ожидание и спектральная плотность k-го входного сигнала (задающего или возмущающего воздействия);  ;
; 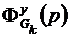 - передаточная функция системы от k-го входа к выходу.
- передаточная функция системы от k-го входа к выходу.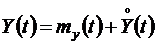 , причем центрированная случайная составляющая описывается дисперсией Dy.
, причем центрированная случайная составляющая описывается дисперсией Dy. . Пусть на систему действуют детерминированное задающее воздействие g(t) и несколько некоррелированных случайных возмущений
. Пусть на систему действуют детерминированное задающее воздействие g(t) и несколько некоррелированных случайных возмущений  , k=1,2,…,K.
, k=1,2,…,K. ,
, ,
,  , Φx(p) - передаточная функция системы по ошибке от задающего воздействия,
, Φx(p) - передаточная функция системы по ошибке от задающего воздействия, 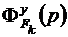 - передаточная функция системы по k-му возмущающему воздействию, k=1,2,...,K.
- передаточная функция системы по k-му возмущающему воздействию, k=1,2,...,K.