
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм розв’язку двоїстим симплексим методом. ⇐ ПредыдущаяСтр 3 из 3
Решение системы линейных уравнений, определяемое базисом, называется псевдопланом задачи, если для любого j. Двойственный симплекс-метод позволяет за конечное число итераций найти оптимальный план двойственно невырожденной задачи, или обнаружить, что множество планов пусто. Теорема 1. Если в псевдоплане, определяемом базисом из mвекторов, есть хотя бы одно отрицательное число, для которого все Координати вектора больше либо равны 0 Теорема 2. Если в псевдоплане, определяемом базисом из m векторов, есть хотя бы одно отрицательное число, для которого хотя бы одна координата вектора меньше 0, то можно перейти к новому псевдоплану, при котором значение целевой функции уменьшится. Теорема 3. При решении задачи двойственным симплекс-методом одновременно строится и оптимальный план другой (двойственной) задачи или устанавливается неограниченность снизу. Алгоритм двойственного симплекс-метода Этап 1 Находим псевдоплан задачи. Этап 2 Проверяем псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану. Этап 3 Выбираем направляющую строку с помощью определения наибольшего по абсолютной величине компоненты плана и направляющий столбец находят при подсчете наименьшей по абсолютной величине отношения элементов строки разностей к соответствующим отрицательным элементам направляющей строки. Этап 4 Находим новый псевдоплан и продолжают действия с этапа 2. Приклад № 1
Решение. 
Выберем в качестве базиса векторы:
Находим величину Направляющая строка - вторая. Тогда по величине
направляющим столбцом будет столбец
План:
Координати:
В результате получили оптимальный план |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 266. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Розглянемо задачу:
Розглянемо задачу: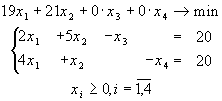 Запишем эту задачу в канонической форме:
Запишем эту задачу в канонической форме: Умножив первое и второе уравнения системы ограничений этой задачи на -1, перейдем к задаче вида:
Умножив первое и второе уравнения системы ограничений этой задачи на -1, перейдем к задаче вида: Построим для этой задачи двойственную:
Построим для этой задачи двойственную: ,
,  .
.

 Находим величину Можно выбрать первую или вторую строку направляющей. Тогда по величине направляющим столбцом будет столбец
Находим величину Можно выбрать первую или вторую строку направляющей. Тогда по величине направляющим столбцом будет столбец ,
, 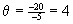 .
. План:
План: Координати:
Координати: В результате:
В результате:
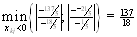
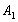 ,
,  .
.
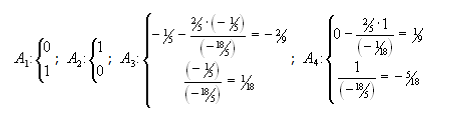

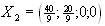 .
.