
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Види математичних моделей двоїстих задач
На підставі розглянутих несиметричних і симетричних двоїстих завдань можна зробити висновок, що математичні моделі пари двоїстих завдань можуть мати один з таких видів .Н е с и м м е т р и ч н ы е з а д а ч и (1) Вихідна задача Двоїста задача Zmin = CX; fmax = YA0; AX = A0; YA £ С. X ³ 0. (2) Вихідна задача Двоїста задача Zmax = CX; fmin = YA0; AX = A0; YA ³ С. X ³ 0. С и м м е т р и ч н ы е з а д а ч и (3) Вихідна задача Двоїста задача Zmin = CX; fmax = YA0; AX ³ A0; YA £ С. X ³ 0. Y ³ 0. (4) Вихідна задача Двоїста задача Zmax = CX; fmin = YA0; AX £ A0; YA ³ С. X ³ 0. Y ³ 0.
Таким чином, перш ніж записати двоїсту задачу для даної вихідної, систему обмежень вихідної задачі необхідно привести до відповідного виду. Запишемо, наприклад, математичну модель двоїстої завдання для наступного вихідної Знайти мінімальне значення лінійної функції Z = 2x1 + x2 + 5x3 при обмеженнях
x1 – 5x2 + x3 ³ 5, xj ³ 0 (j = 1, 2, 3). 2x1 – x2 + 3x3 ³6, Розглянута задача відноситься до симетричних двоїстим задач на відшукання мінімального значення лінійної функції. Для того щоб було можна записати двоїсту задачу, її модель повинна мати вигляд (3). Перехід здійснюється множенням першого нерівності на -1.
Вихідна задача: Zmin = 2x1 + x2 + 5x3 при обмеженнях
 x1 – 5x2 + x3 ³ 5, xj ³ 0 (j = 1, 2, 3). 2x1 – x2 + 3x3 ³6, Двоїста задача: fmin = -4x1 + 5x2 + 6x3 при обмеженнях
y1 – 5y2 - y3 £ 1, yi ³ 0 (i = 1, 2, 3). 2y1 + y2 + 3y3 £ 5, Наведемо без доведення наступну теорему. Теорема 1.1. Якщо при підстановці компонент оптимального плану в систему обмежень вихідної задачі i-тe обмеження звертається в нерівність, то i-та компонента оптимального плану двоїстої задачі дорівнює нулю. Якщо i-та компонента оптимального плану двоїстої задачі позитивна, то i-те обмеження вихідної завдання задовольняється її оптимальним рішенням як суворе рівність 2.1. Основные идеи двойственного симплекс-метода. Безпосередній додаток теорії двоїстості до обчислювальних алгоритмів лінійного програмування дозволило розробити ще один метод вирішення ЗЛП, що отримав назву двоїстого симплекс-методу, або методу послідовного уточнення оцінок. Вперше він був запропонований Лемке в 1954 р. У процесі викладення ідей, покладених в основу двоїстого симплекс-методу, ще раз скористаємося другою геометричною інтерпретацією ЗЛП. Розглянемо деяку КЗЛП (1.48). На рис. 1.11 зображений конус К позитивних лінійних комбінацій розширених векторів умов аj для випадку m = 2, n = 6, а на рис. 1.12 - (для більшої наочності) - поперечний переріз даного конуса деякою площиною L, що проходить паралельно осі аплікат. З кожним планом і завдання, двоїстої по відношенню до (1.48), можна взаємно однозначно пов'язати гіперплоскость, що проходить через початок координат і перпендикулярну вектору (-1, і). Допустимі плани двоїстої задачі (1.49) повинні відповідати умовам ІА ≥ с, які можна переписати у вигляді (1, і) А ≥ 0. Останнє означає, що всякий розширений вектор умов аj лежить «нижче» площини, яка визначається вектором (-1, і). Таким чином, будь-якому допустимому плану двоїстої задачі в даному прикладі відповідає деяка площина, розташована вище всіх розширених векторів, а отже, і конуса К. На рис. 1.12, де зображено поперечний переріз, конусу К відповідає багатогранник, а «гіперплощинами двоїстих планів» - пунктирні лінії, які є їхніми слідами.
За аналогією з інтерпретацією рішення прямої задачі процес рішення двоїстої задачі може бути представлений як пошук такої гіперплощини, яка лежить вище конуса К і перетинає пряму, проведену через кінець вектора b паралельно осі аплікат, в самій нижній точці.
F Надалі систему β={aj1, aj2,...,ajm} з т лінійно-незалежних стовпців матриці умов прямої задачі А будемо називати сполученним базисом, чи двояко допустимим базисом, якщо всякий вектор и Î Rm, задовольняє умовам, задовольняє також умовам иаj≥cj(jÎ1:n), тобто, є допустимим планом двоїстої задачі (1.49). План двоїстої задачі і, відповідний парному базису β={aj1, aj2,...,ajm}, називають опорним планом. Його «опорність» полягає в тому, що в системі обмежень uаj ≥ cj (jÎ1:n), задають область визначення двоїстої задачі D*, т нерівностей з номерами jÎ N(β) звертаються в рівності.
Останній факт є не чим іншим, як геометричною ілюстрацією твердження теореми 1.5. Описані вище властивості пари двоїстих задач лінійного програмування є ідейною основою двоїстого симплекс-методу, який являє собою ітеративний процес цілеспрямованого перебору сполучених (двоїсто припустимих) базисів і відповідних псевдопланів. У цьому й полягає його принципова відмінність від звичайного симплекс-методу, у якому послідовно розглядаються припустимі базисні плани прямої задачі*. Неважко здогадатися, що при певній структурі задачі шлях, запропонований двоїстим алгоритмом, може виявитися більш коротким.
Критерій оптимальності псевдоплану х у двоїстому симплекс-методі полягає в тому, що х одночасно повинен бути пдопустимим планом прямої задачі, тобто всі його компоненти повинні бути невід’ємні (хj ≥ 0).
Але, якщо хоча б одна з компонентів псевдоплану є від’ємною, то процес покращення значення цільової функції може бути продовжений. Геометрична ілюстрація даної ситуації наведена на мал. 1.13. Тут на площині ( для m = 2) зображена система стовпців обмежень КЗЛП, з яких {а1, а2} утворюють поточний базис. Як видно з малюнка, вектор обмежень має від’ємну координату за напрямком, що задається вектором а1. У той же час очевидні й ті базиси (наприклад, {а2, а3}), у яких b буде мати всі додатні координати. Однак це не завжди так. Приклад на мал. 1.14 ілюструє випадок відсутності припустимих планів у прямої задачі: вектор b має від’ємний компонент у поточному базисі {а1, а2} за напрямком а2, а для всіх інших небазисних стовпчиків (а3, а4) дана координата є додатньою, тобто b і стовпчики, що є кандидатами на введення в черговий базис, лежать у різних півплощинах, утворених прямою, що проходить через вектор а1,
і при будь-яких базисах, відмінних від поточного, відповідає координата вектора b однаково залишиться від’ємною. F Таким чином, у двоїстому симплекс-методі ознакою відсутності припустимих планів в розв'язуваної КЗЛП є незаперечність яких-небудь r-х компонент у всіх стовпчиках аj, представлених у поточному базисі β (ar,j(β) ≥ 0, j Î1:n) якщо br(β) < 0 l.*
С другой стороны, если br(β)<0 и в строке аr(β) существуют отрицательные Координати, то псевдоплан можно улучшить выводя из базиса столбец, находящийся на r-м месте, и вводя в него некоторый вектор al, имеющий отрицательную r-ую координату. При наличии в векторе b(β) нескольких отрицательных компонент номер вектора, выводимого из базиса, обычно определяется строкой, содержащей наименьшую (наибольшую по модулю и отрицательную) компоненту. Принцип выбора столбца, вводимого в базис, определяется необходимостью обеспечивать то, чтобы очередной базис определял опорную плоскость, ниже которой располагаются все небазисные векторы. Для этого требуется, чтобы оценки всех небазисных векторов а0,j(β) ( j Î N(β)), вычисляемые по формулам
а0,j(β) = -cj + c(β)аj(β)
(см. (1.26)), оставались положительными. Это, в свою очередь, означает, что номер вводимого столбца l должен быть определен таким образом. Чтобы
После выбора выводимого и вводимого векторов производится обычный пересчет симплекс-таблицы по формулам, аналогичным формулам (1.28)-(1.31), и процесс итеративно повторяется. В результате через конечное число шагов будет найден оптимальный план КЗЛП или установлен факт пустоты множества допустимых планов.
2.2. Алгоритм и табличная реализация двойственного симплекс-метода. Обобщая сказанное в предыдущем пункте, приведем в сжатом виде алгоритм двойственного симплекс-метода для решения КЗЛП.
I-этап. Стандартная итерация алгоритма — выполняется для очередного сопряженного базиса β(q). 1°. Проверка оптимальности текущего псевдоплана: осуществляется просмотр значений bi(β(q)), iÎ1:m. Возможны два варианта: 1΄. Для всех iÎ1:m, bi(β(q)) ≥ 0. Тогда текущий псевдоплан x(β(q)) одновременно является допустимым планом решаемой задачи, т. е. ее оптимальным планом. Вычислительный процесс закончен. Элементы оптимального плана х* определяются по формуле
а достигаемое на нем значение целевой функции равно
1". Существует по меньшей мере один номер строки rÎ1:m, для которого br(β(q))<0 . Следовательно, псевдоплан x(β(q)) — неоптимален. Выбирается строка с номером r, такая, что
Она становится ведущей и определяет номер столбца Nr(β(q)), который должен быть выведен из базиса. Переходим к пункту 2° алгоритма. 2°. Определение столбца, вводимого в базис. Рассматривается ведущая строка аr(β(q)). Возможны два варианта: 2'. Для всех jÎ1: n аr,j(β(q)) ≥ 0. Делается вывод об отсутствии допустимых планов у решаемой задачи (D = Ø) и завершается вычислительный процесс*. 2". В строке аr(β(q)) существует по крайней мере один элемент аr,j(β(q))<0. Согласно правилу (1.62) определяются l — номер столбца, вводимого в очередной базис. Переходим к пункту 3° алгоритма.
По аналогии со стандартным симплекс-методом вычислительную процедуру двойственного симплекс-метода удобно оформлять в виде таблиц, приведенных на рис. 1.5. Очевидно, что с формальной стороны их структура остается неизменной. Иногда считается целесообразным добавить к двойственной симплекс-таблице строку, содержащую строку со значениями λj, которые вычисляются на этапе определения столбца, вводимого в базис.
2.3. Особенности применения двойственного симплекс-метода. Алгоритм двойственного симплекс-метода (как и остальные симплекс-алгоритмы) предполагает знание исходного сопряженного базиса. Очевидно, что в общем случае его нахождение является достаточно непростой задачей, сводящей на нет потенциальные преимущества двойственного алгоритма. Однако в ряде случаев исходный псевдоплан может быть определен достаточно легко. Рассмотрим задачу минимизации:
при обмеженнях
где
Приведем задачу (1.66)-(1.68) к канонической форме, введя фиктивные переменные хn+1, хn+2, ... , хn+m:
Задача, двойственная к (1.70)—(1.72), будет иметь вид:
Из (1.74)-(1.75) очевиден допустимый план двойственной задачи
и исходный сопряженный базис, образуемый векторами аn+1, аn+2, …., аn+m. При этом начальный псевдоплан равен
Таким образом, при решении задачи вида (1.66)-(1.68) двойственный симплекс-метод имеет несомненные преимущества по сравнению с прямым. Другое важное направление использования двойственного симплекс-метода связано с поиском оптимальных планов в тех задачах, условия которых претерпели некоторые изменения после того, как они уже были решены с помощью стандартной симплекс-процедуры. Типичными Прикладами таких изменений являются:
Ø изменение компонент вектора ограничений b, что, допустим, может быть интерпретировано как корректировка объемов доступных ресурсов в процессе управления экономическим объектом; Ø добавление новых ограничений к системе условий задачи, что достаточно часто случается при совершенствовании используемой экономико-математической модели.
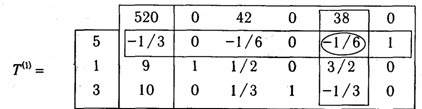
В первом случае, т. е. при изменении вектора b, достоинства двойственного симплекс-метода очевидны, так как ранее найденный оптимальный базис можно использовать в качестве исходного сопряженного базиса при продолжении решения. Второй случай более подробно будет рассмотрен в гл. 4 при рассмотрении методов решения целочисленных задач. В заключение отметим, что в настоящем параграфе был рассмотрен вариант двойственного алгоритма, соответствующий стандартному симплекс-методу. Нетрудно догадаться, что существует и вариант, построенный на базе модифицированного симплекса (схемы, связанной с преобразованием обратных матриц), но, поскольку этот вопрос представляет интерес в основном с точки зрения техники организации вычислений, мы на нем останавливаться не будем. При желании с глубоким и детальным описанием данной версии алгоритма можно ознакомиться в [1]. Отметим лишь, что она обладает теми же принципиальными преимуществами, что и модифицированный симплекс-метод. 2.4. Приклад решения ЗЛП двойственным симплекс-методом. Рассмотрим на конкретном, Прикладе процесс решения КЗЛП двойственным симплекс-методом. Для этого, опять-таки, вернемся к задаче (1.34)-(1.35), решенной в п. 1.4.3 и п. 1.5.2. Предположим, что произошли изменения в векторе ограничений b в результате которых
В результате имеем:
Поскольку b(β(2)) >0, то достигнутый базис N(β(2)) = {4,1,3} является оптимальным. Из Т(2) можно выписать оптимальный план х* = (6, 0, 32/3, 2, 0) и соответствующее ему значение целевой функции f(x*)= 444.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 289. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 x1 – x2 – x3 £ 4,
x1 – x2 – x3 £ 4,


 Слід звернути увагу на те, що не всім сполученим базисам відповідають допустимі базисні плани прямої задачі. Зокрема, вектор b не може бути розкладений з невід'ємними коефіцієнтами по базисам {а1, а2}, {а3 , а4 } чи {а4, а5}. У зв'язку з цим систему коефіцієнтів розкладання вектора b по парному базису називають псевдопланом. В тей же час базис {а2, а3} є допустимим для прямої задачі, і, більше того, з ілюстрації видно, що він, з одного боку, визначає максимум прямої задачі (найвищу точку перетину прямої, що проходить через кінець b, з конусом К), а з іншого - мінімум двоїстої (нижчу точку перетину цієї прямої з лежачою над К опорною гіперплощиною):
Слід звернути увагу на те, що не всім сполученим базисам відповідають допустимі базисні плани прямої задачі. Зокрема, вектор b не може бути розкладений з невід'ємними коефіцієнтами по базисам {а1, а2}, {а3 , а4 } чи {а4, а5}. У зв'язку з цим систему коефіцієнтів розкладання вектора b по парному базису називають псевдопланом. В тей же час базис {а2, а3} є допустимим для прямої задачі, і, більше того, з ілюстрації видно, що він, з одного боку, визначає максимум прямої задачі (найвищу точку перетину прямої, що проходить через кінець b, з конусом К), а з іншого - мінімум двоїстої (нижчу точку перетину цієї прямої з лежачою над К опорною гіперплощиною):



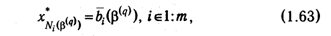



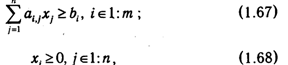

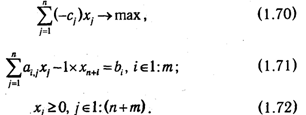




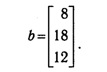


 5,
5, 