
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Несиметричні двоїсті задачі. Теорема двоїстості.Стр 1 из 3Следующая ⇒ Двойственность в линейном программировании
Поняття двоїстості. З кожною задачею лінійного програмування тісно пов'язана інша лінійна завдання, звана двоїстої. Початкове завдання називається вихідною. Зв'язок вихідної і двоїстої задач полягає в тому, що коефіцієнти Cj функції мети вихідної завдання є вільними членами системи обмежень двоїстої задачі, вільні члени Bi системи обмежень вихідної завдання служать коефіцієнтами функції мети двоїстої завдання, а матриця коефіцієнтів системи обмежень двоїстої задачі є транспонованої матрицею коефіцієнтів системи обмежень вихідної задачі. Рішення двоїстої задачі може бути отримано з рішення вихідної і навпаки. Як приклад розглянемо завдання використання ресурсів. Підприємство має т видів ресурсів у кількості bi (i = 1, 2, ..., m) одиниць, з яких виробляється n видів продукцій. Для виробництва 1 од. i-й продукції витрачається aij од. t-гo ресурсу, а її вартість становить Cj од. Скласти план випуску продукції, що забезпечує її максимальний випуск у вартісному вираженні. Позначимо через xj (j = 1,2, ..., n) кількість од. j-й продукций, Тоді вихідне завдання сформулюємо так. Знайти вектор Х =(x1, x2, …, xn), котрий задовольняє обмеженням
a21x1 + a22x2 + … + a2nxn £ b2, xj ³ 0 (j =1,2, ..., n) ………………………………… am1x1 + am2x2 + … + amnxn £ bm,
і доставляє максимальне значення лінійної функції Z = C1x1 + C2x2 + … + Cnxn, Оцінимо ресурси, необхідні для виготовлення продукції. За одиницю вартості ресурсів приймемо одиницю вартості своєї продукції. Позначимо через уi (j = 1,2, ..., m) вартість одиниці i-го ресурсу. Тоді вартість всіх витрачених ресурсів, що йдуть на виготовлення одиниці j-й продукції, дорівнює  Знайти вектор Y =(y1, y2, …, yn), котрий задовольняє обмеженням
a12y1 + a22y2 + … + am2ym £ C2, yj ³ 0 (i =1,2, ..., m) ………………………………… a1ny1 + a2ny2 + … + amnym £ Cm,
і доставляє мінімальне значення лінійної функції f = b1y1 + b2y2 + … + bmym. Розглянуті вихідна і двоїста задачі можуть бути економічно інтерпретовані наступним чином. Вихідне завдання. Скільки і якої продукції xj (j = 1,2, ..., n) необхідно зробити, щоб при заданих вартостях Cj (j = 1,2, ..., n) одиниці продукції і розмірах наявних ресурсів bi (i = 1 , 2, ..., n) максимізувати випуск продукції у вартісному вираженні. Двоїста задача. Яка повинна бути ціна одиниці кожного з ресурсів, щоб при заданих кількостях ресурсів bi і величинах вартості одиниці продукції Ci мінімізувати загальну вартість затрат? Змінні уi називаються оцінками або обліковими, неявними цінами. Багато задач лінійного програмування спочатку ставляться як вихідних чи двоїстих задач, тому має сенс говорити про пару двоїстих задач лінійного програмування.
Несиметричні двоїсті задачі. Теорема двоїстості.
У несиметричних двоїстих завданнях система обмежень вихідної задачі задається у вигляді рівностей, а двоїстої - у вигляді нерівностей, причому в останній змінні можуть бути і негативними. Для простоти доказів постановку завдання ус-ловімся записувати в матричній формі. Вихідне завдання. Знайти матрицю-стовпець X= (x1, x2, …, xn), яка задовольняє обмеженням (1.1) AX = A0, Х ³ 0
і мінімізує лінійну функціюZ=СХ. Двоїста задача. Знайти матрицю-рядок Y= (y1, y2, …, ym), яка задовольняє обмеженням (1.2) YA £ С і максимізує лінійну функцію f = YA0 В обох задачах C= (c1, c2, …, cn) - матриця-рядок, A0 = (b1, b2, …, bm) — матриця-стовпець, А= (aij) — матриця коефіцієнтів системи обмежень. Зв'язок між оптимальними планами пари двоїстих задач встановлює наступна теорема. Теорема (теорема двоїстості). Якщо з пари двоїстих Завдання одне володіє оптимальним планом, то й інша має рішення, причому для екстремальних значень лінійних функцій виконується співвідношення min Z = max f. Якщо лінійна функція одної з задач не обмежена, то інша не має рішення. Доведення. Припустимо, що вихідна задача має оптимальний план, який отримано симплекс методом. Не порушуючи спільності, можна вважати, що остаточний базис складається з т перших векторів A1, A2, ..., Am. Тоді остання симплекс таблиця має вигляд табл. 1.1. Т а б л и ц я 1.1
Нехай D — матриця, складена з компонент векторів остаточного базису A1, A2, ..., Am; тоді табл. 1.1 складається з коефіцієнтів розкладання векторів A1, A2, ..., An вихідної системи по векторах базису, тобто кожному вектору Aj в цій таблиці відповідає такий вектор Xj що (1.3) Aj= DXj(j= 1,2, ,.., n) . Для оптимального плана отримуєм (1.4) A0 = DX*, де X* = (x*1, x*2, …, x*m). Позначимо через (1.5) A = D (1.6) A0=DX*; D-1A0 = X*, (1.7) min Z= C*X*, (1.8) де С* = (C*1, C*2, …, C*m), С = (C1, C2, …, Cm, Cm+1, …, Cn), a Оптимальний план вихідної задачі має виглядX* = D-1 А0, тому оптимальний план двоїстої задачі шукаємо у вигляді: (1.9) Y* = C*D-1. Покажемо, що Y* дійсно план двоїстої задачі. Для цього обмеження (1.2) запишемо у вигляді нерівності YA — С £ 0, в ліву частину якого підставимо Y*. Тоді на підставі (1.9), (1.5) та (1.8) отримуємо Y* А – С = С* D-1А – С = С* Звідки знаходимоY*A £ С. Так як Y* задовольняє обмеженням (1.2), то це і є план двоїстої задачі. При цьому в плані значення лінійної функції двоїстої завдання f (Y *) = Y * A0. Враховуючи співвідношення (1.9), (1.6) і (1.7), маємо (1.10) f(Y*) = Y*A0 = C*D-1 A0 = C*X* = min Z(X). Таким чином, значення лінійної функції двоїстої завдання від Y * чисельно дорівнює мінімальному значенню лінійної функції вихідної задачі. Доведемо тепер, що Y* є оптимальним планом. Помножимо (1.1) на будь-який план Y двоїстої завдання, а (1.2) - на будь-який план X вихідної завдання: YAX=YA0=f (Y), YAX £ СХ = Z (X), звідси випливає, що для будь-яких планів Х іY виконується нерівність (1.11) f (Y) £ Z (X). Цим же співвідношенням пов'язані і екстремальні значення max f (Y) min Z£ (Х). З останнього нерівності укладаємо, що максимальне значення лінійної функції досягається тільки у випадку, якщо max f (Y) = min Z (X), але це значення [см. (1.10)] f (Y) досягає при плані Y *, отже, план Y * - оптимальний план двоїстої задачі. Аналогічно можна довести, що якщо двоїста задача має рішення, то вихідна також має рішенням і має місце співвідношення max f (Y) = min Z (X). Для доказу другої частини теореми припустимо, що лінійна функція вихідної завдання не обмежена знизу. Тоді з (1.11) випливає, що f(Y) £ -¥ . Цей вираз позбавлене сенсу, отже, двоїста задача не має рішень. Аналогічно припустимо, що лінійна функція двоїстої завдання не обмежена зверху. Тоді з (1.11) отримуємо, що Z (X) ³ +¥. Цей вираз також позбавлено сенсу, по-цьому вихідна задача не має рішень. Доведена теорема дозволяє при вирішенні однієї з двоїстих завдань знаходити оптимальний план іншої. Вихідна задача. Знайти мінімальне значення лінійної функції Z = x2 – x4 – 3x5 при обмеженнях
- 4x2 + x3 + 2x4 – x5 = 2, xij ³ 0 (j = 1, 2, …, 6) 3x2 + x5 + x6 = 5, Тут мятриця-рядок С = (0;. 1; 0; —1; — 3, 0), матриця-стовпець
A0 = 2 A = 0 -4 1 2 -1 0 3 0 3 0 0 1 1
2 -4 3 A’’ = 0 1 0 -1 2 0 1 -1 0 0 0 1 Двоїста задача. Знайти максимальне значення лінійної функції f = y1 + 2y2 +5 y3 при обмеженнях
2y1 – 4y2 + 3y3 £ 1, y2 £ 0, -y1 + 2y2 £ -1, y1 – y2 + y3 £ -3, y3 £ 0.
Решение исходной задачи находим симплексным методом (табл. 1.2).
Оптимальний план вихідної задачіX* = (0; 1/3; 0; 11/3; 4; 0), при якому Zmin = - 46/3, отриманий у четвертій ітерації табл. 1.2. Використовуючи цю ітерацію, знайдемо оптимальний план двоїстої задачі. Згідно теоремі подвійності оптимальний план двоїстої задачі знаходиться зі співвідношення Y* =C*D-1, де матрицяD-1 - матриця, зворотна матриці, складеної з компонент векторів, що входять в останній базис, при якому отримано оптимальний план вихідної задачі. Минулий базис входять вектори A5, A4, A2; значить,
D = (A5, A4, A2)= -1 2 -4 1 0 3 Зворотній матрицяD-1 утворена з коефіцієнтів, що стоять в стовпцяхA1, A3,A6 четвертої ітерації:
D-1 = -1/3 1/3 2/3 -2/3 -1/3 1/3
2 1 0 Y = С*D-1= (-3; -1; 1) · -1/3 1/3 2/3 -2/3 -1/3 1/3 Y*=(-19/3; -11/3; -1/3), тобто. yi = С*Хi, де Хi — коефіцієнти розкладання останньої ітерації, що стоять в стовпцях векторів первісного одиничного базису. Отже, i-ту двоїсту зміну можна отримати з значення оцінки (m + 1)-й рядки, стоїть проти відповідного вектора, що входив в початковий одиничний базиc, якщо до неї додати відповідне значення коефіцієнта лінійної функції: у1 = — 19/3 + 0 = — 19/3; y2 = -11/3 + 0 = -11/3; у3 = -1/3+0 = -1/3. При цьому план max f = -46/3.
Симетричні двоїсті задачі Різновидом двоїстих задач лінійного, програмування є двоїсті симетричні завдання, в яких система обмежень як вихідної, так і двоїстої задач задається нерівностями, причому на двоїсті змінні накладається умова не заперечності. Вихідна задача. Знайти матрицю-стовпець Х = (x1, x2, …, xn), яка задовольняє системі обмежень (1.12). АХ>А0, Х>0 і мінімізує лінійну функцію Z = СХ. Двоїста задача. Знайти матрицю-рядок Y = (y1, y2, …, yn), яка задовольняє системі обмежень YA £ C, Y ³ 0 і максимізує лінійну функцію f = YA0. Систему нерівностей за допомогою додаткових змінних можна перетворити в систему рівнянь, тому будь-яку пару симетричних двоїстих завдань можна перетворити на пару несиметричних, для яких теорема подвійності вже доведена. Використовуючи симетричність, можна вибрати завдання, зручніше для рішення. Обсяг завдання, розв'язуваної за допомогою ЕОМ, обмежений числом включаємих рядків, тому завдання, досить громіздке у вихідній постановці, може бути спрощена в двоїстому формулюванні. При обчисленнях без допомоги машин використання двоїстості спрощує обчислення. Вихідна задача. Знайти мінімальне значення лінійної функції Z = x1 + 2x2 + 3x3 при обмеженнях
x1 - x2 - 4x3 £ -3, xi ³ 0 (i=1,2,3) x1 + x2 - 2x3 ³ 6, 2x1 + x2 - 2x3 ³ 3, Очевидно, для того щоб записати двоїсту задачу, спочатку необхідно систему обмежень вихідної завдання привести до вигляду (1.12). Для цього другу нерівність слід помножити на -1. Двоїста задача. Знайти максимум лінійної функції f = 2y1+ 3y2 + 6y3 + 3y4 при обмеженнях
2y1 + y2 + y3 + y4 ³ 2, -y1+ 4y2 - 2y3 - 2y4 ³ 3, Для рішення вихідної завдання необхідно ввести чотири додаткові перемінні і після перетворення системи - одну штучну. Таким чином, вихідна симплексная таблиця буде складатися з шести рядків і дев'яти стовпців елементи яких підлягають перетворенню. Двоїсту задачу вирішуємо симплексним методом (табл. 1.3). Оптимальний план двоїстої задачі Y* = (0; 1/2; 3/2; 0), fmax = 21/2. Оптимальний план вихідної задачі знаходимо, використовуючи оцінки (m + 1)-го рядка останньої ітерації, які знаходяться в стовпцях A5, A6, A7 : x1 = 3/2 + 0 = 3/2; x2 = 9/2 + 0 = 9/2; x3= 0+ 0 = 0. При оптимальному плані вихідної задачіX* = (3/2; 9/2; 0) лінійна функція досягає найменшого значення: Zmin =21/2. Т а б л и ц а 1.3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 237. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 a11x1 + a12x2 + … + a1nxn £ b1,
a11x1 + a12x2 + … + a1nxn £ b1, . Вартість витрачених ресурсів не може бути менше вартості остаточного продукту, тому має виконуватися нерівність
. Вартість витрачених ресурсів не може бути менше вартості остаточного продукту, тому має виконуватися нерівність  . Отже, двоїсту задачу можна сформулювати наступним чином.
. Отже, двоїсту задачу можна сформулювати наступним чином. a11y1 + a12y2 + … + am1ym £ C1,
a11y1 + a12y2 + … + am1ym £ C1,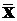 матрицю, складену з коефіцієнтів розкладання векторів Аj (j = 1, 2, ..., n), записанних в табл. 1.1. Тоді, враховуючи співвідношення (1.3) и (1.4), отримуємо:
матрицю, складену з коефіцієнтів розкладання векторів Аj (j = 1, 2, ..., n), записанних в табл. 1.1. Тоді, враховуючи співвідношення (1.3) и (1.4), отримуємо: = C*
= C*  x1 + 2x2 - x4 + x5 = 1,
x1 + 2x2 - x4 + x5 = 1,
 1 1 2 0 -1 1 0
1 1 2 0 -1 1 0 1 0 0
1 0 0 y1 £ 0,
y1 £ 0, 1 -1 2
1 -1 2 2 1 0
2 1 0 З цієї ж ітерації слідуєС* = (— 3; —1; 1). Таким чином
З цієї ж ітерації слідуєС* = (— 3; —1; 1). Таким чином 2x1 + 2x2 - x3 ³ 2,
2x1 + 2x2 - x3 ³ 2, 2y1 - y2 + y3 + 2y4 £ 1,
2y1 - y2 + y3 + 2y4 £ 1,