
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Имитационное моделирование. ⇐ ПредыдущаяСтр 4 из 4 Проведем имитацию исполнения контракта при оптимальных значениях стимулирующих выплат. Поскольку результаты деятельности фирмы в модели получены при допущении, что доход есть случайная величина, распределение которой зависит от усилий агента, необходимо имитировать её многократную реализацию. Каждая реализация соответствует малому периоду времени, по истечению которого происходит подведение итогов, с определением заработной платы агента и определением прибыли фирмы. Исходные данные Выбор величины дохода
Чтобы обеспечить реализацию этой случайной величины в MS Excel используем функцию СЛЧИС(), которая вычисляет значения равномерно распределенной случайной величины в интервале [0;1]. Пусть число будет иметь искомое распределение. Решение приведено на рис. 11-16. На рис. 11. приведены расчеты по аналитическим формулам, (ЧЧ).
Рис. 11. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Имитационное моделирование исполнения контракта при оптимальных значениях стимулирующих выплат (начало).
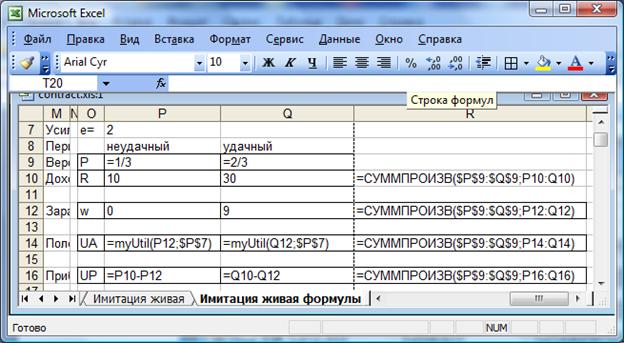
Рис. 12. Фрагмент электронных таблиц MS Excel в режиме отображения формул. Имитационное моделирование исполнения контракта при оптимальных значениях стимулирующих выплат (начало).
Сам процесс имитации реализован в строках ниже 34. Подведение итогов имитации приведено в строках 19-33. Такое расположение итогов (выше самой имитации) позволяет при необходимости увеличить количество имитируемых периодов, вставив необходимое количество строк или дописав их в конец, без сильного изменения итогов.  При имитации каждому периоду времени соответствует одна строчка таблицы. Всего промоделировано 500 временных периодов. В интервалах N34:N534 и O34:O534 содержатся реализации искомых случайных величин
Рис. 13. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Имитационное моделирование, многократного повторения производственного периода (продолжение).
Рис. 14. Фрагмент электронных таблиц MS Excel в режиме отображения формул. Имитационное моделирование, многократного повторения производственного периода (продолжение).
Подведение итогов моделирования и сравнение с расчетными результатами приведено на рис.15.-16. Анализ показал, что количество неудачных и удачных периодов при 500 повторениях производственного цикла равно 162 и 338 соответственно, а доли в общем количестве повторений равны 0,324 и 0,676 соответственно. Доли незначительно отличаются от теоретических(вероятностей) , отклонения равны 2.80% и 1.4% соответственно. Это показывает что при таком количестве повторений реализация случайной величины – дохода фирмы проведена корректно. Средние значения дохода фирмы, заработной платы работника, прибыли фирмы и полезности работника по результатам имитации находятся в интервале ячеек О27:R27 соответственно. Сравнение этих средних значений с вычисленными значениями по основным формулам проведено в интервале ячеек О30:R30. Очевидно, что они несущественно отличаются, так отклонения лежат в диапазоне от 0,80% для величины дохода фирмы до 2,80% для полезности работника. Наличие отклонений обусловлено случайностью величины дохода фирмы. Более точные значения можно, как правило, получить, увеличив количество имитаций.
Рис.15. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Подведение итогов имитационного моделирования и сравнение с расчетными результатами (окончание).
Рис. 16. Фрагмент электронных таблиц MS Excel в режиме отображения формул. Подведение итогов имитационного моделирования и сравнение с расчетными результатами (окончание).
Проведем имитацию исполнения контракта при отсутствии стимулирующих выплат. Процесс имитации аналогичен случаю, рассмотренному выше за исключением того, что выплаты работнику не являются случайной величиной, а являются константой равной
Рис. 17. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Имитационное моделирование исполнения контракта при отсутствии стимулирующих выплат (начало).
Рис. 18. Фрагмент электронных таблиц MS Excel в режиме отображения данных. Подведение итогов имитационного моделирования исполнения контракта при отсутствии стимулирующих выплат и сравнение с расчетными результатами (окончание)
Анализ показал, что количество неудачных и удачных периодов при 500 повторениях производственного цикла равно 337 и 167 соответственно, а доли в общем количестве повторений равны 0,666 и 0,334 соответственно. Доли незначительно отличаются от теоретических (вероятностей), отклонения равны 0.10% и 0.2% соответственно. Это показывает что при таком количестве повторений реализация случайной величины – дохода фирмы проведена корректно. Средние значения дохода фирмы, заработной платы работника, прибыли фирмы и полезности работника по результатам имитации находятся в интервале ячеек C27:F27 соответственно. Сравнение этих средних значений с вычисленными значениями по основным формулам проведено в интервале ячеек C30:F30. Очевидно, что заработная плата и полезности работника являются постоянными величинами и полностью совпадают с расчетными значениями. Величины дохода и прибыли фирмы отличаются на 0,08% и 0,09% соответственно, что можно расценить как несущественное отклонение. Наличие отклонений обусловлено случайностью величины дохода фирмы, ещё более точные значения можно, как правило, получить, увеличив количество имитаций. Выводы.
Задание на курсовую работу. Студентам предлагается одна из двух задач. Первая элементарная, представляющая собой модификацию задачи, разобранной выше. Вторая задача предполагает некоторую самостоятельную работу. При выборе задачи 1 студент может рассчитывать только на оценку «удовлетворительно». Во всех задачах требуется
Указание:
Задача 1. Определить наилучший контракт с точки зрения фирмы в следующих условиях. Все буквенные обозначения, введенные ранее, остаются в силе. Альтернативная стоимость работы, определяемая рыночной ставкой заработной платы, такова, что её полезность равна Функция полезности для работника имеет следующий вид:
Целевой функцией для фирмы является величина чистого дохода, т.е. величина дохода минус величина вознаграждения работника
Уровень усилий работника может принимать два значения, 1 и 2.
Рис. 20. Возможный доход фирмы в зависимости от состояния рынка (удачности или неудачности периода) при высоком уровне усилий работника.
Значения параметров a, b, c, d и u задаются преподавателем в зависимости от варианта. Задача 2. Постановка задачи
1. 2. 3. 4. Минимальное значение функции полезности для агента составляет Umin. При более низком значении агент стремится сменить место работы. Доход фирмы R является случайной величиной и зависит от уровня усилий агента S следующим образом: 1. При интенсивной работе агента Smax, высокий доход фирмы Rуд.max, случается с вероятностью Pуд.max. низкий доход фирмы Rуд.min, случается с вероятностью Pуд.min. 2. При отлынивании агента Smin, высокий доход фирмы Rнеуд.max, случается с вероятностью Pнеуд.max. низкий доход фирмы Rнеуд.min, случается с вероятностью Pнеуд.min.
Таблица 1
Варианты заданий.
РЕКОМЕНДАТЕЛЬНЫЙ БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Приложение1 Элементы теории контрактов В настоящее время экономическая теория предлагает более реалистическое описание самого процесса принятия решений, чем это предпринималось раньше. Стандартная неоклассическая модель изображает человека как существо гиперрациональное. Один из новых подходов (Неоинституциональный) отличается большей трезвостью. Это находит выражение в двух его важнейших поведенческих предпосылках --ограниченной рациональности и оппортунистического поведения. Первая отражает факт ограниченности человеческого интеллекта. Знания, которыми располагает человек, всегда неполны, его счетные и прогностические способности далеко не беспредельны, совершение логических операций требует от него времени и усилий. Одним словом, информация ресурс дорогостоящий, поэтому агенты вынуждены останавливаться не на оптимальных решениях, а на тех, что кажутся им приемлемыми исходя из имеющейся у них ограниченной информации. Их рациональность будет выражаться в стремлении экономить не только на материальных затратах, но и на своих интеллектуальных усилиях. При прочих равных условиях они будут предпочитать решения, предъявляющие меньше требований к их предсказательным и счетным возможностям. Оппортунистическое поведение определяется О.Уильямсоном, который ввел это понятие в научный оборот, как "преследование собственного интереса, доходящее до вероломства" (self-interest-seeking-with-guile). Речь идет о любых формах нарушения взятых на себя обязательств, например -- уклонении от условий контракта. Индивиды, максимизирующие полезность, будут вести себя оппортунистически (скажем, предоставлять услуги меньшего объема и худшего качества), когда это сулит им прибыль. Одной из основных формы оппортунистического поведения является отлынивание. "Отлынивание" (shirking): оно возникает при асимметрии информации, когда агент точно знает, сколько им затрачено усилий, а принципал имеет об этом лишь приблизительное представление (так называемая ситуация "скрытого действия"). В таком случае возникает и стимул, и возможность работать не с полной отдачей. Особенно остро встает эта проблема, когда люди работают сообща ("командой") и личный вклад каждого определить очень трудно. Приложение 2 Строгое решение нелинейной задачи определяемой соотношениями (24), (25),(26), (27) может быть получено с использованием теоремы Куна-Таккера. Для этого введем новые переменные Целевая функция (24) примет вид (П.1),
Ограничение (17) преобразуется к виду
Ограничение (20) преобразуется к виду
Ограничение (23) преобразуется к виду
Очевидно, что решение оптимальное решение задачи (П.1)-(П.4) достигается в той же точке, что и решение задачи определяемой соотношениями (24), (25),(26), (27). Область допустимых значений функции нелинейной оптимизации (П.1)-(П.4) в координатах
Рис.П1. Область допустимых значений задачи нелинейной оптимизации в координатах Введем функции
Преобразуем соотношения (П.2) и (П.4) используя вновь введенные функции. Ограничения (П.4) преобразуется к виду
Ограничение (П.2) преобразуется к виду
Область допустимых значений функции нелинейной оптимизации в координатах
Рис.П2. Область допустимых значений задачи нелинейной оптимизации в координатах Все функции ограничений-неравенств афинны, Для проверки выпуклости вычислим её Гессиан (матрицу вторых производных).
. Главные миноры равны Вычислим градиенты функций задачи.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 будем осуществлять с помощью генератора случайных чисел, который генерирует значение случайной величины, имеющей следующее распределение:
будем осуществлять с помощью генератора случайных чисел, который генерирует значение случайной величины, имеющей следующее распределение: является значением функции СЛЧИС(),тогда величина
является значением функции СЛЧИС(),тогда величина 





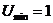 . В условиях не симметричности информации работник ожидаемо работает с низким уровнем усилий
. В условиях не симметричности информации работник ожидаемо работает с низким уровнем усилий 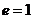 . Результаты расчетов приведены на рис. 17-18.
. Результаты расчетов приведены на рис. 17-18.

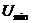 равна u.
равна u.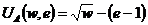
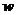 .
.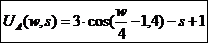

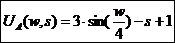
 Рассматриваются два индивида – поручитель (принципал, патрон) P и исполнитель (агент) A. Агент может выполнять свои договорные обязательства с разным уровнем усилий S, например, работать интенсивно (Smax) или отлынивать (Smin). Зарплата агента W составляет минимальную ставку Wmin или повышенную (премиальную) ставку Wmax. Функция полезности для агента UA, определяющая его заинтересованность в данной работе, определяется по номеру формулы Nф для каждого варианта. Номера формул функций полезности:
Рассматриваются два индивида – поручитель (принципал, патрон) P и исполнитель (агент) A. Агент может выполнять свои договорные обязательства с разным уровнем усилий S, например, работать интенсивно (Smax) или отлынивать (Smin). Зарплата агента W составляет минимальную ставку Wmin или повышенную (премиальную) ставку Wmax. Функция полезности для агента UA, определяющая его заинтересованность в данной работе, определяется по номеру формулы Nф для каждого варианта. Номера формул функций полезности: и
и 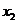 , где
, где  и
и  .
.




 ,
,  и
и  используя соотношения, приведенные ниже.
используя соотношения, приведенные ниже.




 и направление градиента в некоторых точках.
и направление градиента в некоторых точках.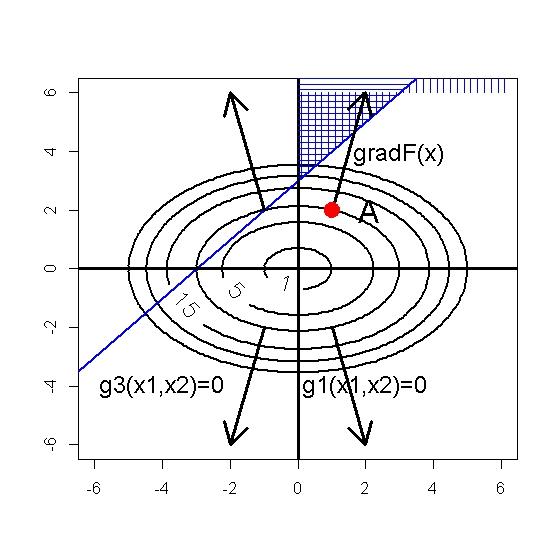
 а значит, выпуклы, поэтому область допустимых значений в задаче выпукла. Заметим, что если взять некоторую точку внутри области, например,
а значит, выпуклы, поэтому область допустимых значений в задаче выпукла. Заметим, что если взять некоторую точку внутри области, например, 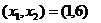 , то эта точка будет допустимой и все неравенства в ней выполняются строго
, то эта точка будет допустимой и все неравенства в ней выполняются строго  . Отсюда следует что область регулярна во всех точках.
. Отсюда следует что область регулярна во всех точках.
 и
и  положительны, поэтому по критерию Сильвестра матрица положительна определена. Поскольку для выпуклости дважды дифференцируемой функции необходимо и достаточно неотрицательной определенности Гессиана, то функция
положительны, поэтому по критерию Сильвестра матрица положительна определена. Поскольку для выпуклости дважды дифференцируемой функции необходимо и достаточно неотрицательной определенности Гессиана, то функция 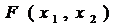 выпукла во всей области определения. Таким образом, условия Куна-Таккера будут необходимыми и достаточными условиями, определяющими решение задачи.
выпукла во всей области определения. Таким образом, условия Куна-Таккера будут необходимыми и достаточными условиями, определяющими решение задачи.
