
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Асимметричная информация об усилияхРассмотрим ситуацию, в которой принципал не может четко отслеживать (анализировать) величину усилий агента,другими словами, усилия агента являются ненаблюдаемыми для принципала, а свои усилия агент знает сам. Т.о. существует асимметричная информация об усилиях. Проанализируем базовый контракт в новой ситуации. Значение функции полезности агента имеет следующий вид при низком уровне усилий
Т.е. полезность для агента при базовом контракте и низком уровне усилий агента выше, чем при базовом. В этом случае агент проявляет оппортунистичность своего поведения. Несовпадение интересов принципала и агента проявляется в том, что первый заинтересован в высоком уровне усилий агента, поскольку это положительно влияет на его ожидаемый результат, тогда как последний заинтересован в низком уровне усилий, т.к. усилия отрицательно влияют на его полезность. Таким образом, задача заключается в нахождении таких условий контракта, которые бы максимизировали полезность принципала, одновременно стимулируя агента выбирать нужный уровень усилий. Для этого нужно решить задачу на нахождение условного максимума полезности принципала с учетом ограничений участия и самоотбора при двух уровнях усилий агента. Чтобы добиться повышенного уровня усилий работника, необходимо изменить базовый контракт таким образом, чтобы в случае большей величины дохода фирмы зарплата работника также возрастала бы. Другими словами говоря, контракт должен быть стимулирующим, т.е. если фирме необходимо, чтобы агент постоянно работал с высоким уровнем усилий(  Обозначим через
Ожидаемая полезность
Легко заметить, что стимулирующая оплата работника будет действенной, если полезность в случае высокого уровня усилий определяемая соотношением (13) будет не меньше полезности в случае низкого уровня усилий, определяемой соотношением (14), т.е.
Выражение типа (15) называется ограничением совместимости по стимулам, которое представляет собой условие, ориентирующее агента на использование высокого уровня усилий. Важным является то, что полезность, получаемая агентом при выборе усилий, желательных для принципала будет не меньше полезности получаемой агентом при любых других усилиях. Т.о. агенту не выгодно проявлять свою оппортунистичность. Заметим, что выражение (15), с учетом (13) и (14) можно преобразовать к виду
Упростив это выражение, получаем
При любом контракте должно выполняться ограничение на участие (дающее возможность агенту получить альтернативную работу),
Соотношение (18)с учетом (13) и того что
Преобразуя (19) получаем
Значение функции полезности
Очевидно, что для принципала ситуация будет оптимальной, когда
Ограничения определяются условиями (17) (ограничением совместимости по стимулам),(20)( ограничение на участие), к которым следует добавить естественное ограничение – неотрицательность фазовых переменных
Решение нелинейной задачи определяемой соотношениями (22), (17),(20), (23) может быть упрощено путем введения новых переменных Целевая функция (22) примет вид (24),
Ограничение (17) преобразуется к виду
Ограничение (20) преобразуется к виду
Ограничение (23) преобразуется к виду
Целевая функция, определяемая соотношением (24) является квадратичной, а ограничения (25),(26) и (27) - линейны, поэтому (есть основания предполагать, что ) данная задача нелинейной оптимизации является задачей квадратичного программирования. Решение этой задачи может быть получено графически. Очевидно, что линиями уровня целевой функции (24) в пространстве координат
На рис.4. линия уровня соответствующая значению
Рис.3. Графическое решение задачи нелинейной оптимизации в координатах
Рис.4. Графическое решение задачи нелинейной оптимизации в координатах
Поскольку Вычислим значение функции полезности
Другим разумным вариантом контракта для принципала в случае не наблюдаемости усилий агента является назначение ему минимальной заработной платы равной единице Поскольку Вычислим ожидаемую полезность
Решим задачу нелинейного программирования с помощью надстройки «Поиск решения» (рис. 5-9). Для этого в ячейки D5: D6, где будут находиться значения искомых величин Для удобства вычислений запишем функцию в VBA (Visual Basic for Application) MyUtil для вычисления полезности агента. При использовании этой функции на листе MS Excel эта функция будет отображаться в разделе «Определенные пользователем». Заметим, что эта функция вычисляет только значение выражения В ячейке F12 вычислим ожидаемую полезность
Рис. 5. Фрагмент электронных таблиц MS Excel в режиме отображения данных (начало) для решения примера 1 В ячейке F22 вычислим ожидаемую полезность
.
Рис. 6. Фрагмент электронных таблиц MS Excel в режиме отображения данных (окончание) для решения примера 1.
Рис. 7. Фрагмент электронных таблиц MS Excel. Функция, определенная пользователем, MyUtil для вычисления полезности агента.
Рис. 8. Фрагмент электронных таблиц MS Excel в режиме отображения формул (начало) для решения примера 1.
Для проведения оптимизации используем надстройку «Сервис» Þ «Поиск решений». В диалоговом окне заполняем поля, как показано на рис. 10. Ограничение $F$12>=$F$22 отражает необходимость выполнения ограничения совместимости по стимулам (15), а ограничение $F$12>=$F$3 отражает необходимость выполнения ограничения на участие (18). Выполнение естественного ограничения (23) (неотрицательность фазовых переменных
Рис.10. Диалоговое окно надстройки «Поиск решения» при поиске оптимальных значений стимулирующих выплат
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 316. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
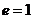 и величине вознаграждения
и величине вознаграждения 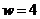 .
.
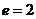 ), то контракт должен быть таким, что ожидаемая полезность агента в этом случае была выше, чем при низком уровне усилий (
), то контракт должен быть таким, что ожидаемая полезность агента в этом случае была выше, чем при низком уровне усилий (  величину заработной платы, которую получает агент при неудачном периоде для фирмы (когда у фирмы низкий уровень дохода
величину заработной платы, которую получает агент при неудачном периоде для фирмы (когда у фирмы низкий уровень дохода  ). Обозначим через
). Обозначим через  величину заработной платы, которую получает агент при удачном периоде для фирмы (когда у фирмы высокий уровень дохода
величину заработной платы, которую получает агент при удачном периоде для фирмы (когда у фирмы высокий уровень дохода  ). Вычислим ожидаемую полезность
). Вычислим ожидаемую полезность  для агента в этом случае при высоком уровне усилий (
для агента в этом случае при высоком уровне усилий ( 
 для агента в случае низкого уровня усилий (
для агента в случае низкого уровня усилий ( 




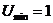
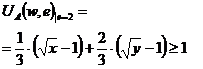


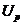 для принципала при высоком уровне усилий агента в условиях, когда зарплата агента не постоянна, будет вычисляться с помощью соотношения
для принципала при высоком уровне усилий агента в условиях, когда зарплата агента не постоянна, будет вычисляться с помощью соотношения 
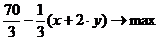

 и
и  , где
, где  и
и  .
.



 и
и  (рис.4). Через эту точку проходит эллипс, который является линией уровня соответствующая значению
(рис.4). Через эту точку проходит эллипс, который является линией уровня соответствующая значению  , поскольку справедливо следующее соотношение.
, поскольку справедливо следующее соотношение. 


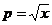 и
и  .
. для принципала при высоком уровне усилий агента (
для принципала при высоком уровне усилий агента (  и
и  (29)
(29)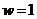 . В этом случае полезность принципала может быть вычислена с помощью соотношения (10) и будет равна
. В этом случае полезность принципала может быть вычислена с помощью соотношения (10) и будет равна 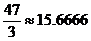
 , то принципалу выгодней заключать стимулирующий контракт, при уровнях зарплаты агента (
, то принципалу выгодней заключать стимулирующий контракт, при уровнях зарплаты агента ( 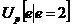 может быть вычислено по формуле (11) и она равна
может быть вычислено по формуле (11) и она равна  . Поскольку
. Поскольку 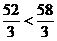 мы приходим к выводу, что принципал делится своей прибылью с агентом, заключая стимулирующий контракт.
мы приходим к выводу, что принципал делится своей прибылью с агентом, заключая стимулирующий контракт. для агента при высоком уровне усилий (
для агента при высоком уровне усилий ( 
 для агента.
для агента. , при произвольных значениях аргументов
, при произвольных значениях аргументов 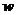 и
и 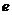 , но не вычисляет среднюю (ожидаемую) полезность для агента, которая наиболее интересна при решении задачи.
, но не вычисляет среднюю (ожидаемую) полезность для агента, которая наиболее интересна при решении задачи. для агента при высоком уровне усилий .
для агента при высоком уровне усилий .


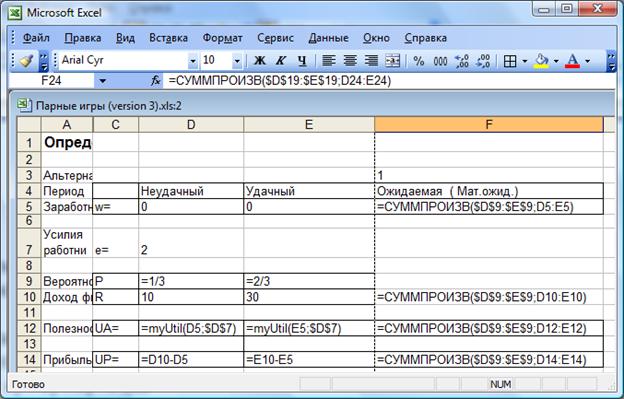
 Рис. 9. Фрагмент электронных таблиц MS Excel в режиме отображения формул (окончание) для решения примера 1.
Рис. 9. Фрагмент электронных таблиц MS Excel в режиме отображения формул (окончание) для решения примера 1.