
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы решения дискретных задач ⇐ ПредыдущаяСтр 4 из 4 Мы убедились, что с помощью булевых переменных можно решать часто встречающиеся задачи оптимизации. Но как решать? Есть три метода решения задач с булевыми переменными: ■ метод ветвей и границ; ■ метод сплошного перебора; ■ метод фильтрующего ограничения. Методом ветвей и границ задачи дискретного программирования решаются, как обычные задачи целочисленного программирования. При этом на каждую переменную накладывается два требования:
Совершенно очевидно, что выполнение этих двух требований обеспечивает получение в решении значений Пример 4. Требуется решить систему методом сплошного перебора: max L = 3
Решение. Так как Таблица 5.
1. Заполнить все возможные сочетания допустимых значений 2. Определить и записать значения левых частей ограничений (1)-(4) и целевой функции. 3. Вычеркнуть те варианты, в которых не удовлетворяется хотя бы одно ограничение, как приводящие к недопустимым решениям. 4. Из оставшихся вариантов принимается тот, в котором целевая функция максимальна. В примере max L = 8 — в шестом варианте (оптимальном), в котором  Из этого примера видно, что в данном случае всего вариантов будет 23 = 8 и для каждого варианта надо вычислить четыре ограничения и целевую функцию, т. е. выполнить N = 8(4 + 1) = 40 вычислительных операции. Значит, в общем случае N = 2n(m + 1), где n — число переменных, m – число ограничений. Следовательно, при увеличении размерности задачи число вычислений резко возрастает (табл. 6). Таблица 6.
Для сокращения трудоемкости полного перебора применяют различные методы. Метод фильтрующего ограничения предполагает следующую последовательность действий. 1. Принимают некоторые значения 2. Определяют значение целевой функции при таком на боре переменных L = 3 3. Далее устанавливают новые значения переменных и целевой функции; причем если полученная целевая функция меньше 3, то этот вариант не рассматривают. Дли исключения возможного рассмотрения такого варианта, вводят дополнительное ограничение 3 4. Составляют таблицу (табл. 7), в которой для каждого варианта проверяют выполнение всех ограничений, включая Ф. Если вычисление прекращается и величины не определены, то в клетках таблицы ставится прочерк. Введение фильтрующего ограничения Ф привело к сокращению числа вычисляемых величин (24 вместо 40, т. е. 60%).
Число вычислений можно уменьшить, если фильтр будет не постоянным для всего цикла вычислений, а изменяющимся, т. е. если в ходе вычислений при каком-либо наборе переменных значение целевой функции окажется лучше, чем у фильтра, то это новое допустимое решение принимают для следующих вычислений в качестве нового фильтра. Такой фильтр называют адаптивным. Например, из таблицы видно, что в пятом варианте Ф = 5. Поэтому для дальнейших вычислений в качестве фильтрующего ограничения принимаем 3
Заключение При выполнении данной курсовой работы были получены навыки решения специальных задач линейного программирования, а также рассмотрены модели оптимизации и этапы принятия решений. В этой работе был осуществлен обзор и анализ специальных задач линейного программирования, описана полная классификация и структура математических методов.
Список используемой литературы 1. Глухов В. В., Медников М. Д., Коробко С. Б. Математические методы и модели для менеджмента.2-е изд., испр. и доп. – СПб.: Издательство «Лань», 2005. – 5 с. – (Учебники для вузов. Специальная литература). 2. «Исследование операций в экономике»: Учебное пособие для вузов / Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н.: под ред. проф. Кремера Н. Ш. – М.: ЮНИТИ, 2004 3. Харчистов Б.Ф. Методы оптимизации: Учебное пособие. - Таганрог: Изд-вo ТРТУ, 2004. - 140с. 4. «Линейное и нелинейное программирование» под общей редакцией профессора Ляшенко И. Н., Киев – 1975 5. «Математические методы и модели в коммерческой деятельности»: Учебник, 2-е изд., перераб. и дополн. / Фомин Г. П. – М: Финансы и статистика, 2005 6. «Математические методы и модели исследования операций»: Учебное пособие / Кутузов А. Л. – издательство СПб ГПУ, 2005 7. «Математические методы: Учебник» / Партика Т. Л., Попов И. И. – М: ФОРУМ: ИНФРА, 2005
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 501. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 [0; 1] т. е. равных 0 или 1.
[0; 1] т. е. равных 0 или 1. 1 - 2
1 - 2 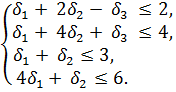
 =
=  = 1;
= 1;  .
.