
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение задачи методом ГомориВо многих экономических задачах переменные выражают физически неделимые объекты и потому могут принимать только натуральные значения. Соответственно, в таких задачах на переменные накладывается дополнительное требование их целочисленности.
Присоединяя равенство (1.1) к ранее решенной задаче, получить новую задачу линейного программирования, которую вновь решить симплексным методом. Если ее оптимальное решение окажется целочисленным, то оно и будет оптимальным решением исходной задачи. Если снова получится нецелочисленное решение, то построить новое сечение, и т.д. Пример.Найти наибольшее значение функции
при ограничениях:
Метод ветвей и границ Задача линейного программирования решается без учета целочисленности. Такая задача называется непрерывной. Далее рассматривают одну из переменных xj, на которую накладывают ограничение целочисленности, но которая получила дробное значение. На основе полученного решения составляют дополнительные ограничения: xj ≤ [ где [ Полученное решение новых задач проверяют на целочисленность переменных. Если решение не удовлетворяет требованию целочисленности, на основе каждой из задач составляют, аналогично предыдущим, две новые и т. д. Если одно из решений удовлетворяет требованию целочисленности, значение целевой функции принимается за граничное Lгр. При этом рассмотрение других задач продолжается до тех нор, пока не будет получено:  ■ на одной из ветвей недопустимое решение; ■ на одной из ветвей целочисленное решение. Тогда значение целевой функции сравнивается с Lгр (верхним - при max, нижним - при min); если полученное значение хуже, оно отбрасывается; если лучше, то принимается за граничное; ■ на одной из ветвей нецелочнеленное решение, однако при этом значение целевой функции хуже граничного. Тогда дальнейшее рассмотрение также прекращается. На первом цикле расчета
Таким образом, для получения целочисленного решения методом ветвей и границ приходится решать большое число задач линейного программирования, причем в каждом очередном ветвлении число ограничений увеличивается на 1. Поэтому время решения задачи целочисленного программирования по сравнению с непрерывной значительно увеличивается. Пример 1. max L = 7x1 + 3x2,
Решение. В результате решения задачи симплекс-методом найдем оптимальное решение В полученном решении x2 = 7,5 — нецелочисленное. Поэтому для дальнейшего решения составляем две новые задачи с различными граничными условиями. Задача 2. Задача 3. max L = 7x1 + 3x2, max L = 7x1 + 3x2,
Результаты решения симплекс методом задачи 2: В задаче 1 переменная Результаты решения непрерывной и целочисленной задачи вводятся в таблице 1. В качестве оптимального принимается решение задачи 5, которое дает наибольшее из целочисленных решений значение целевой функции.
Таблица 1.
Из примера видно, что метод ветвей и границ достаточно трудоемкий. При этом оптимальное решение может быть получено в результате сравнения всех допустимых целочисленных решений. Поэтому при решении задач реальной размерности может потребоваться память, которой нет даже в современных компьютерах, или потребуется практически неприемлемое время решения. Обязательное условие метода — наличие верхних границ на значения переменных Dj. Если Dj не назначена, то ее определяют по зависимости:
Где
Задача выбора вариантов Перейдем теперь к частному случаю задач целочисленного программирования — задаче выбора вариантов. В этом частном случае искомая переменная С помощью булевых переменных можно решать самые различные по содержанию задачи, в которых надо что-то выбирать из имеющихся различных вариантов (например, еще в первобытнообщинном строе глава племени наверняка решал такую задачу, выбирая, какого члена общины на какую работу поставить), в том числе: задачи о назначении, выбора вариантов, дискретного программирования. Пример 2. В задаче выбора вариантов примем, что для получения результата в виде максимально возможной прибыли необходимы два видя ресурсов: материальные и трудовые. Возможны четыре варианта расхода ресурсов и получения прибыли (табл. 2). Требуется выбрать, какие варианты принять для реализации при условии, чтобы общее число принятых вариантов не превышало трех (k Решение. Для составления модели примем, что j-му варианту будет соответствовать
Тогда математическая модель задачи запишется: max L = 65
Последняя строка системы обеспечивает выполнение условия, чтобы общее число принятых вариантов не превышало трех. Из результатов решения этой задачи (первый столбец табл. 3) видна, что наибольшая прибыль (max L = 300) будет получена в том случае, если будут приняты третий и четвертый варианты.
С помощью булевых переменных можно накладывать дополнительные логические связи между вариантами. Например, требуется, чтобы четвертый вариант был принят только в том случае, если принят второй; а если же второй вариант не принят, то и четвертый не должен быть принят. Это условие можно записать так: Может быть сформулирован и другой вариант дополнительных условий. Например, требуется, чтобы был принят либо третий вариант, либо четвертый, т. е. Сравнивая значение прибыли в оптимальном решении (max L = 300) с прибылью при выполнении дополнительных условий, можно сделать вывод, что они, как всегда, приводят к снижению прибыли. Переходя от примера с дополнительными условиями к общему случаю, задачу выбора вариантов можно записать так: Max L =
где последнее ограничение может учитывать самые разнообразные условия. Если накладывается требование «должен», то в ограничении ставится знак равенства: Если требование «может», то — знак неравенства, в частности: ■ если накладывается требование «И», то
например, принятие и первого и третьего вариантов запишется ■ если для вариантов накладывается требование «ИЛИ», то условие запишется:
Следовательно, если принять, что
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 679. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (1.1)
(1.1)

 ]и xj ≥ [
]и xj ≥ [ 

 = 1;
= 1;  = 7,5; L1 = 29,5, где верхний индекс переменных — номер задачи.
= 7,5; L1 = 29,5, где верхний индекс переменных — номер задачи.

 = 1,2;
= 1,2;  = 7; L2 = 29,4; задачи 3:
= 7; L2 = 29,4; задачи 3:  = 0,75;
= 0,75;  = 8; L3 = 29,25;
= 8; L3 = 29,25; = 1 — целочисленная, а в последующих задачах при целочисленности х2 перестала быть целочисленной x1. Затем следует накладывать ограничения целочисленности на x1 и т. д. (рис. 2).
= 1 — целочисленная, а в последующих задачах при целочисленности х2 перестала быть целочисленной x1. Затем следует накладывать ограничения целочисленности на x1 и т. д. (рис. 2).
 ;
;

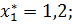
 ;
;


 ;
;



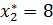 ;
;



 минимальные значения всех
минимальные значения всех  , для которых определяется верхняя граница
, для которых определяется верхняя граница  .
. . И это уже будет означать, что в результате решения задачи
. И это уже будет означать, что в результате решения задачи 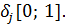 Такие переменные обычно называют булевыми (в честь предложившего их английского математика Джорджа Буля, 1815-1864).
Такие переменные обычно называют булевыми (в честь предложившего их английского математика Джорджа Буля, 1815-1864). 3).
3).
 + 80
+ 80  +
+  + 210
+ 210  ,
,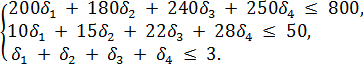
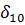



 (результат решения в третьем столбце).
(результат решения в третьем столбце).

 (число принятых вариантов «должно быть» три).
(число принятых вариантов «должно быть» три).
 ;
;
 соответствует «быть»,
соответствует «быть»,  — «не быть», то извечный вопрос «быть или не быть» запишется
— «не быть», то извечный вопрос «быть или не быть» запишется  = 0 означает «быть»;
= 0 означает «быть»;  = 0,
= 0,  = 1 — означает «не быть». Так как целевая функция не сформулирована, то дать оптимальный ответ на этот вопрос невозможно. Чтобы принять решение, необходимо знать, чего мы хотим. Но об этом мы уже неоднократно говорили.
= 1 — означает «не быть». Так как целевая функция не сформулирована, то дать оптимальный ответ на этот вопрос невозможно. Чтобы принять решение, необходимо знать, чего мы хотим. Но об этом мы уже неоднократно говорили.