
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дискретное программированиеВ задачах дискретного программирования результатом решения должны быть целые, но не любые целые. Пример 3. Мебельная фабрика выпускает диваны, кресла и стулья. Требуется определить, сколько можно изготовить спинок диванов, подлокотников кресел и ножек стульев при известном удельном расходе ресурсов (табл. 4)., чтобы доход был максимальным. Таблица 4.
Причем выпуск спинок дивана может принимать любое значение, подлокотники изготавливаются парами, т. е. их количество должно быть кратно двум, а количество ножек стульев — четырем. Решение. С учетом этих требований математическая модель задачи запишется:
где Здесь дополнительное введение булевых переменных дает возможность обеспечить выпуск изделий в кратном заданном количестве. Так, для подлокотников x2 может принимать следующие значения: если в результате решения будет получено Для решения задачи с учетом дополнительных условий мы ввели еще семь переменных и четыре ограничения. Следовательно, введение дополнительных требований привело к увеличению размерности задачи. Заметим, что если бы нам требовалось определить выпуск спинок, подлокотников и ножек для одного изделия (комплекта), то можно было бы записать x2 = 2х1; х3 = 4x1 и не вводить дополни тельных ограничений и булевых переменных. Но это была бы другая задача.  В результате решения задачи были получены следующие значения: max L = 320; При этом оказались не полностью использованы ресурсы: резерв первого равен 50, второго — 4 ед. Такое недоиспользование характерно для задач целочисленного программирования, т. е. ресурс, остается, но для использования на увеличение дискретного количества продукции его оказывается недостаточно. В общем виде задачу распределения ресурсов с учетом требования дискретного значения переменных можно записать: max(min)
где max(min)
Значит, в данном случае, как и всегда, за удовлетворение дополнительных требований приходится платить увеличением размерности задачи и целочисленностью.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 516. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||
 L =
L = 


 10,
10,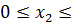 10,
10, 10,
10,


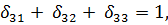
 - варианты количества подлокотников и ножек (k = 1, …, ki).
- варианты количества подлокотников и ножек (k = 1, …, ki). , а остальные
, а остальные  то x2; если
то x2; если  , а остальные
, а остальные  , то x2 = 4 и т.д.
, то x2 = 4 и т.д. = 1;
= 1;  = 4;
= 4;  = 12;
= 12; 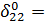
 0;
0;

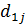 ,
,  , …,
, …,  , … — дискретные значения, которые может принимать переменная
, … — дискретные значения, которые может принимать переменная  . Эта система отличается от обычной задачи распределения ресурсов появлением булевых переменных и увеличением числа ограничений:
. Эта система отличается от обычной задачи распределения ресурсов появлением булевых переменных и увеличением числа ограничений: