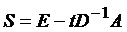Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Для решения системы рассмотрим одношаговый стационарный метод ⇐ ПредыдущаяСтр 3 из 3
при n=0,1,2…. Предположим, что задан начальный вектор решения. Тогда метод (1.24) сходится, если норма вектора
Теорема. Условие сходимости итерационного метода. Пусть А - симметричная положительно определенная матрица и выполнено условие D - 0.5tA > 0 (где t > 0). Тогда метод (1.24) сходится. Следствие 1.Пусть А - симметричная и положительно определенная матрица с диагональным преобладанием, то есть:
при j=1,2,…,m. Тогда метод Якоби сходится. Следствие 2. Пусть А - симметричная и положительно определенная матрица с диагональным преобладанием, тогда метод верхней релаксации сходится при (0< w<2). Проверяется, при каком w - метод достигает заданной точности быстрее. В частности, при w=1 метод верхней релаксации превращается в метод Зейделя, следовательно, при w=1 метод Зейделя сходится. Теорема. Итерационный метод (1.24) сходится при любом начальном векторе x0 тогда и только тогда, когда все собственные значения матрицы по модулю меньше единицы. Плохо обусловленные системы линейных алгебраических уравнений
Дана система линейных алгебраических уравнений
Ах=В. (2.1)
Если система плохо обусловлена, то это значит, что погрешности коэффициентов матрицы А и правых частей B или же погрешности их округления сильно искажают решение системы. В качестве примера рассмотрим систему
Решение этой системы x1 » 1.981 x2 » 0.4735.
Оценим влияние погрешности правых частей на результат. Рассмотрим “возмущенную” систему с правой частью b* = (2.505 , 2.415) и решим эту систему:  x1* » 2.877 x2* » -0.4629.
Относительная погрешность правой части d (в) = 0.005/2.51 » 0.28% привела к относительной погрешности решения d (x*) =0.9364/1.981 » 47.3%. Погрешность возросла примерно в 237 раз. Число обусловленности системы (2.1) приблизительно равна 237. Подобные системы называются плохо обусловленными. |
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 199. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1.24)
, (1.24)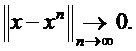
 ,
,