Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Количество строк и столбцов соответствует порядку характеристического уравнения
Чтобы система была устойчива, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и все n главных диагональных миноров матрицы Гурвица были положительны. Число определителей Гурвица равно порядку характеристического уравнения п. Критерий Гурвица применяют при n ≤ 5. При больших порядках возрастает число определителей, и процесс становится трудоемким. Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Автоматическая система, описываемая характеристическим уравнением
устойчива, если при a0>0 положительны все определители ∆1, ∆2, . . .∆п вида
Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, то система неустойчива. Если главный определитель ∆п=0, а все остальные определители положительны, то система находится на границе устойчивости. Рассмотрим частные случаи критерия Гурвица для n=1;2;3;4. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия. 1. Для уравнения первого порядка (n=1)
условие устойчивости: а0>0 и ∆1=а1>0, т.е. для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля. 2. Для уравнения второго порядка (n=2)
условие устойчивости:
Т.о., и для системы второго порядка необходимое условие устойчивости (положительность коэффициентов) является одновременно и достаточным. 3. Для уравнения третьего порядка (n=3)
условие устойчивости:
При n=3 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля и произведение средних коэффициентов уравнения (а1, а2) было больше произведения крайних (а0, а3). 
4. Для уравнения четвертого порядка (n=4)
кроме положительности всех коэффициентов требуется выполнение условия
При n=4 система будет устойчива при всех коэффициентах больших нуля и при
Т.о., для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель ∆п-1 были положительными. Критерий Гурвица удобно использовать при n<5. При n>5 критерий Гурвица становится громоздким и применяют критерий Рауса.
Тема № 11 Определение степени устойчивости систем по заданной ПФ Пример. Передаточная функция разомкнутой системы задана в виде: W(s) = k/s(T1s +1)(T2s +1) Исследовать устойчивость системы. Р е ш е н и е . Характеристическое уравнение замкнутой системы D(p)=0, где D(p) =1+W(s) s = p . Откуда следует p(T1p+1)(T2p+1)+ k = 0 Раскрыв скобки, получим T1T2p3 + (T1 + T2)p2 + p + k = 0. Тогда имеем: a0 = T1 T2 ; a1 = (T1 + T2); a2 = 1; a3 = k. Коэффициенты характеристического уравнения положительны. Составляем матрицу Гурвица и найдем определители этой матрицы. Для устойчивости системы все они должны быть положительными: Δ1 = a1, откуда (T1 + T2) > 0; Δ2 = a1×a2 − a0 ×a3, откуда (T1 + T2) − kT1T2 > 0; !!!!!!!!!!!!!!!!!!!!!!!!! Δ3 = a1×a2×a3 − a0×a32 = a3( a1×a2 − a0×a3 ), откуда a3 >0 , то есть k > 0
Условие устойчивости по критерию Гурвица получает вид: (T1 + T2) > kT1*T2 или Границы устойчивости: 1) an = 0, k = 0; 2) Δn-1 = 0, 3) a0 = 0, T1*T2 = 0. Тема № 12 Определение запаса устойчивости систем по ЛАФЧХ При частотных критериях устойчивости различают два критерия: по амплитуде и по фазе. Запас устойчивости по амплитуде определяется наиближайшей точкой по отношению к критической. В численном значении - это длина отрезка [0;B], где В – точка пересечения годографа системы и отрицательной оси. Нормированная величина запаса устойчивости:
Если Если Если На практике считается допустимым запас по амплитуде в логарифмическом масштабе - Чтобы определить, обладает ли САУ заданным запасом устойчивости по амплитуде, проводится следующие исследования: 1. Строится годограф амплитудно-фазовой характеристики разомкнутой системы. 2. Определяется ближайшая точка пересечения данного годографа с действительной осью по отношению к точке [-1,0]. 3. Определяется запас устойчивости по формуле: 4. Если полученный запас устойчивости больше заданного, то САУ отвечает заданному запасу устойчивости, в противном случае САУ не обладает заданным запасом.
На практике допустимым запасом устойчивости считается угол: Если Если
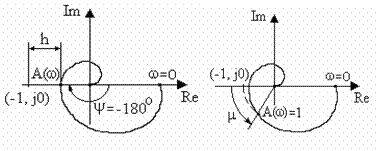
запасы устойчивости системы, которые характеризуют близость амплитудно-фазовой частотной характеристики разомкнутой системы к точке с координатами (-1, j0). Запасы устойчивости определяют на двух частотах: частоте среза ωс и критической частоте ωкр. На частоте среза АЧХ разомкнутой системы равна единице, на критической частоте ФЧХ принимает значение, равное -π. Различают запас устойчивости по амплитуде (модулю) и запас устойчивости по фазе. Запас устойчивости по амплитуде задается некоторой величиной h (рис.5.12,а), на которую должен отличаться модуль АФЧХ разомкнутой системы от единицы на частоте, при которой фаза равняется -1800, т.е. ( ) = -1800 h = 1-A( ) ψ ω ω . (5.14
а) б) Рис. 5.12. АФЧХ разомкнутой системы Запас устойчивости по фазе задается некоторым углом μ (рис.5.12,б), на который должна отличаться фаза АФЧХ разомкнутой системы от -1800 на частоте, при которой модуль равняется единице, т.е. μ = -180 -ψ (ω ) A(ω ) =1 0 . (5.15) В хорошо демпфированных системах запас устойчивости по амплитуде составляет примерно 6÷20 дб, что составляет 2÷10 в линейном масштабе, а запас по фазе − 30÷600.
Оценка устойчивости по ЛЧХ Построение амплитудно-фазовых частотных характеристик разомкнутых систем связано с громоздкими вычислениями, поэтому целесообразно оценивать их устойчивость по логарифмическим частотным характеристикам. Для этого необходимо построить ЛЧХ разомкнутой системы (рис.5.14). На рис.5.14 условно показано четыре варианта возможного прохождения ЛФХ. В том случае, когда АФЧХ не имеет точек пересечения с вещественной осью слева от точки с координатами (-1, j0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы выполнялось условие ωс< ωкр. То есть замкнутая система будет абсолютно устойчивой, если ЛАХ разомкнутой системы принимает отрицательные значения раньше, чем ЛФХ достигнет значения фазы -1800 (кривая 4 на рис.5.14). Если ЛАХ разомкнутой системы принимает отрицательные значения позже, чем ЛФХ достигнет значения фазы -1800 (кривая 1 на рис.5.14), то замкнутая система неустойчивая. Если ЛАХ разомкнутой системы принимает значение амплитуды 0 дб на одной частоте, что и ЛФХ достигнет значения фазы -1800 (кривая 2 на рис.5.14), то это соответствует колебательной границе устойчивости. В условно устойчивых системах (кривая 3 на рис.5.14) для оценки устойчивости следует в диапазоне частот, где ЛАХ больше нуля, подсчитать число переходов ЛФХ через прямую -1800. Если число положительных (сверху вниз) переходов через эту прямую равняется числу отрицательных (снизу вверх), то система в замкнутом состоянии устойчива.
Рис. 5.14. ЛЧХ разомкнутой системы: 1 - система неустойчива; 2 - система нейтральная; 3 - система условно устойчивая; 4 - система абсолютно устойчивая По ЛЧХ разомкнутой системы можно определить запасы устойчивости: запас по фазе μ отсчитывается по ЛФХ на частоте среза ωс, а запас по амплитуде Lh соответствует значению ЛАХ на критической частоте ωкр, взятому с обратным знаком (кривая 4 на рис.5.14). Если ωс=ωкр, то система находится на границе устойчивости. Граничное значение общего коэффициента передачи разомкнутой системы kгр определяется из выражения 20 lg kгр = 20 lg k + Lh, где k - общий коэффициент передачи разомкнутой системы. В заключение дадим некоторые рекомендации, которые следуют из практики проектирования систем. Во-первых, для того чтобы в системе были обеспечены необходимые запасы устойчивости, наклон ЛАХ в диапазоне частот, в котором расположена частота среза, должен быть равным -20дб/дек. При наклоне характеристики, равном -40дб/дек, трудно обеспечить необходимый запас устойчивости по фазе. При наклоне характеристики, равном 0 дб/дек, получают излишне большие запасы устойчивости по фазе, система становится передемпфированной с длительным переходным процессом. Во-вторых, запас устойчивости по фазе в системе зависит от диапазона частот, в котором ЛАХ разомкнутой системы на частоте среза имеет наклон -20дб/дек. Чем больше этот диапазон частот, тем выше запас устойчивости по фазе и наоборот.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 229. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

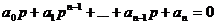 ,
,

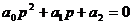




 .
. .
.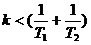
 ;
;
 - запас устойчивости по модулю.
- запас устойчивости по модулю. , то система находится на границе устойчивости;
, то система находится на границе устойчивости; , то система устойчивая;
, то система устойчивая; - система неустойчива.
- система неустойчива. , что составляет
, что составляет 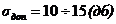 .
. , где h – это отрезок [0;B].
, где h – это отрезок [0;B]. Запасом устойчивости по фазе называется минимальный угол, образуемый отрицательной действительной осью и прямой, соединяющий начало координат и точку пересечения годографа амплитудно-фазовой характеристики разомкнутой системы и окружности с единичным радиусом с центром в начале координат.
Запасом устойчивости по фазе называется минимальный угол, образуемый отрицательной действительной осью и прямой, соединяющий начало координат и точку пересечения годографа амплитудно-фазовой характеристики разомкнутой системы и окружности с единичным радиусом с центром в начале координат. .
. , то система не обладает запасом устойчивости;
, то система не обладает запасом устойчивости; , то система обладает запасом устойчивости
, то система обладает запасом устойчивости