
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Временные характеристики САУСтр 1 из 7Следующая ⇒ МАТЕРИАЛ К ТЕСТАМ Тема № 1 1.Передаточная функция Уравнение динамики в операторной форме:
Дифференциальный оператор W(p) называют передаточной функцией. Передаточная функцияесть отношение изображений по Лапласу его выходной и входной величин при нулевых начальных условиях. Она определяет зависимость отношения выходной величины звена к входной во времени: W(p) = y(t)/u(t), т.е. динамический коэффициент усиления. Передаточные функции в операторной форме также представляют собой сокращенную символическую запись дифференциальных уравнений. В установившемся режиме d/dt = 0, p = 0, и передаточная функция превращается в коэффициент передачи звена K = bm /an. Знаменатель передаточной функции D(p) = a0pn+a1pn-1+a2pn -2+...+an называют характеристическим полиномом. Его корни, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функцией. Числитель K(p) = b0pm+b1pm-1+...+bm называют операторным коэффициентом передачи. Его корни, при K(p) = 0 и W(p) = 0, называются нулями передаточной функции.
2. Изображения Лапласа и Фурье. Частотной характеристикой динамического звена называют функцию комплексного аргумента jw, полученную путем формальной замены s на jw в выражении передаточной функции (Это соответствует переходу от изображения Лапласа к изображению Фурье.) Таким образом, частотную характеристику динамического звена можно определить как отношение спектра (преобразования Фурье) выходного сигнала к спектру входного сигнала.
3. Перерегулирование
Перерегулирование - это процентное соотношение разницы максимального перерегулирования и установившегося значения: 
4. Воздействия К внешней среде системы управления относятся процессы, оказывающие влияние на поведение управляемого объекта. Среда является источником помех измерения dj(t), возмущающих воздействий fj(t), внешних задающих воздействий. К возмущающим относят воздействия, препятствующие функционированию объекта. Это могут быть силы сопротивления или трения для кинематических механизмов, температура окружающей среды для тепловых процессов и т. д. Возмущающие воздействия объединяются в вектор возмущений. Сигнал y*(t), определяющий требуемый закон движения системы, называется задающим воздействием Сигнал e(t) = y*(t) – y(t), характеризующий текущее значение отклонения выходной переменной от задающего воздействия, называется рассогласованием, отклонением или ошибкой управления. Задачи стабилизации и слежения иначе могут быть сформулированы как задачи поддержания нулевого значения рассогласования, т. е. e(t) → 0. Временные характеристики САУ Наиболее наглядное представление о динамических свойствах элемента дает его переходная функция (характеристика). Переходной функцией h(t)называют изменение выходной величины y(t) во времени, возникающее после подачи на вход единичного ступенчатого воздействия, при нулевых начальных условиях.
Импульсной переходной функцией w(t) называют изменение выходной величины y(t), возникающее после подачи на вход дельта – функции, при нулевых начальных условиях (см. рис.). Эту функцию называют также функцией веса.
и наоборот, переходная функция равна интегралу от импульсной переходной:
Переходные характеристики h(t) и w(t) называют также временными.
Тема № 2 Определение дифуравнения системы по уравнению ПФ и наоборот
- знаменатель дифуравнения ПФ представить выражением, где операторы заменены соответствующими производными выходного сигнала - y и приравнять его к числителю, где также операторы заменены соответствующими производными входного сигнала - u.
Например, если задана ПФ вида: То дифуравнение системы будет иметь вид:
Для получения дифуравнения ПФ в операторном виде выполняется обратная прцедура.
Тема № 3 Частотные характеристики САУ Зависимость отношения амплитуд выходного и входного сигнала от частоты ещё называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А(w)Амплитудная частотная характеристика (АЧХ) при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности симметрична относительно оси ординат.
Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ) и обозначают j(w) (см. рис.3.5). Аналитические выражения А(w) и j(w) называют соответственно амплитудной и фазовой частотными функциями.
АЧХ дает отношение амплитуд выходного и входного сигналов, A(w) = Um /Ym = |W(jw)| = Амплитудная частотная характеристика (АЧХ) показывает, как пропускает звено сигнал различной частоты, иначе, представляет собой коэффициент изменения амплитуды гармонических колебаний при прохождении через звено (рис. 3.4). – симметрична относительно оси ординат.
Рис. 3.4. Амплитудная частотная характеристика
где характеристика достигает максимума, иначе, на этой частоте звено имеет максимальный коэффициент усиления;
уменьшаясь, принимает значение, равное единице, и при дальнейшем повышении частоты остается меньше единицы;
характеристика, уменьшаясь, принимает значение, равное 0,707, и при дальнейшем повышении частоты не увеличивается;
ФЧХ - сдвиг по фазе выходной величины относительно входной: j(w) = arctg(Q(w)/P(w)).
Рис. 3.5. Фазовая частотная характеристика
Каждому фиксированному значению частоты wi соответствует комплексное число W(jwi), которое на комплексной плоскости можно изобразить вектором, имеющим длину А(wi) и угол поворота j(wi) (см. рис.в). Отрицательные значения j(w), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси. При изменении частоты от нуля до бесконечности вектор W(jw) поворачивается вокруг начала координат, при этом одновременно увеличивается или уменьшается длина вектора. Кривая, которую при этом опишет конец вектора, называемая годографом, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты. Проекции вектора W(jw) на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначают
При этом, действительная частотная характеристика Р(w) – всегда четная функция частоты, а мнимая характеристика Q(w) – всегда нечетная функция.
Мнимая частотная характеристика (МЧХ). Представляет собой зависимость мнимой составляющей частотной передаточной функции от частоты (рис.3.7). Симметрична относительно начала координат.
Рис. 3.7. Мнимая частотная характеристика Из рис. 3.3. следует, что правильными формулами связывающими модуль частотной передаточной функции (A), фазовый сдвиг (f), вещественную (U) и мнимую (V) части частотной передаточной функции являются:
Амплитудная фазовая частотная характеристика (АФЧХ) при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности (рис.д) симметрична относительно оси абсцисс(рис.3.3)., т.к.параметром на кривой годографа является частота, изменяющаяся в интервале от 0 до ∞. Для произвольной частоты ω радиус вектор в точке W(jω) показывает амплитуду выходного сигнала, а угол j(ω) - сдвиг фазы между выходным и входным сигналом.
Рис.3.3
Тема № 4 1. Логарифмичекие амплитудно-частотные характеристики САУ При практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик. За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением wi и его десятикратным значением 10wi. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1. Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)
ординаты которой измеряют в логарифмических единицах – белах (Б) или децибелах (дБ). При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс. Так как А( Верхняя полуплоскость ЛАХ соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость - значениям А<1 (ослабление амплитуды).При построении логарифмической фазовой частотной характеристики (ЛФХ)отсчет углов
Тема № 5 1. Характеристики типовых динамических звеньев
Информация данной таблицы позволяет установить название типового динамического звена по его Дифуравнению или по его Передаточной функции. Тема № 6 1. Реакции типовых динамических звеньев на единичное ступенчатое входное воздействие По заданной ПФ определяется тип звена, затем находится реакция звена и его переходная функция ( в тестах в ПФ вместо s стоит p ) !!!
Тема № 7
* По переходной характеристике, представленной на рисунке, можно определить постоянную времени Т по точке пересечения касательной к кривой h(t) с ее асимптотой и передаточный коэффициент k, равный установившемуся значению h(t) –пересечение с осью ординат, умноженному на значение T. * Колебательные функции с одинаковой амплитудой симметричны относительно передаточного коэффициента k (т.е его значение находится посредине ординаты). А определить постоянную времени Т можно по соотношению
И при частоте w=1 также равен 1.
Для звена с ПФ
Тема № 8 Определение результирующих ПФ при различном соединении звеньев Возможны три способа соединения звеньев: последовательное, параллельное и встречно-параллельное или соединение с обратной связью (ОС).
Последовательное соединение блоков. Последовательным называют такое соединение звеньев, при котором выходная величина предыдущего звена является входной для последующего (рис. 3.6.1). При известных передаточных функциях звеньев, можно записать: W(p) = W1(p) W2(p). Таким образом, систему из неограниченного количества звеньев, включенных последовательно, можно заменить одним эквивалентным звеном с передаточной функцией W(p) равной произведению передаточных функций звеньев.
Параллельное соединение блоков. При параллельном соединении звеньев на все входы подается одна и та же величина, а выходная величина равна сумме выходных величин отдельных звеньев (рис. 3.6.2). W(p) = W1(p)+W2(p). Из последнего выражения следует, что параллельное соединение звеньев эквивалентно одному звену с передаточной функцией, равной сумме передаточных функций, входящих в соединение звеньев.
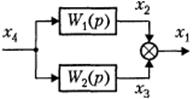
Система с отрицательной обратной связью. При встречно-параллельном соединении звеньев на вход звена кроме входной подается еще и выходная величина через специальное звено обратной связи. На рис. 3.6.3 звено W1(p) составляет прямую цепь, которая охвачена ОС, звеном W2(p). При этом если сигнал x3 вычитается из входного сигнала x4, то ОС называется отрицательной, а если суммируется, то ОС – положительная. Для отрицательной обратной связи передаточная функция: W(p) = W1(p) /(1+ W1(p)W2(p)). (3.6.1)
Тема № 9 Определение устойчивости линейных динамических систем по их уравнениям 1.Устойчивость линейной динамической системы может быть определена по характеру cвободного движения. 2.Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением
где Система является устойчивой, если свободная составляющая xc(t) переходного процесса с течением времени стремится к нулю, т.е. если
Такая устойчивость называется асимптотической.
Если свободная составляющая неограниченно возрастает, т.е. если
Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости. Общее условие устойчивости: Для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательны. Используя геометрическое представление корней на комплексной плоскости (см. рис.) в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости(эквивалентную основной): Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости. Если хотя бы один корень находится в правой полуплоскости, то система будет неустойчивой. Мнимая ось jb является границей устойчивости в плоскости корней. Если характеристическое уравнение имеет одну пару чисто мнимых корней (pk=+jbk, pk+1=-jbk), а все остальные корни находятся в левой полуплоскости, то в системе устанавливаются незатухающие гармонические колебания с круговой частотой Точка b =0 на мнимой оси соответствует так называемому нулевому корню. Если уравнение имеет один нулевой корень, то система находится на апериодической границе устойчивости. Если таких корня два, то система неустойчива.
. Таким образом, исследование устойчивости системы сводится к определению знаков вещественных частей корней характеристического уравнения системы. Тема № 10 Определение устойчивости систем по критерию Гурвица Из коэффициентов характеристического уравнения строится определитель Гурвица D по алгоритму: 1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an; 2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз; 3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 322. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

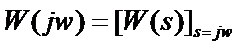

 .
.

 Импульсная переходная функция w(t) равна производной от переходной функции h(t):
Импульсная переходная функция w(t) равна производной от переходной функции h(t): ,
,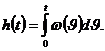
 Чтобы из дифуравнения ПФ, представленного в операторном виде, найти дифуравнение системы необходимо:
Чтобы из дифуравнения ПФ, представленного в операторном виде, найти дифуравнение системы необходимо: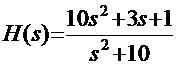 ,
, 
 ,
,

 - резонансная частота, т.е. частота, на которой амплитудная частотная
- резонансная частота, т.е. частота, на которой амплитудная частотная
 с - частота среза, частота, на которой амплитудная частотная характеристика,
с - частота среза, частота, на которой амплитудная частотная характеристика, - полоса пропускания, диапазон частот гармонических колебаний, пропускаемых звеном без заметного ослабления.
- полоса пропускания, диапазон частот гармонических колебаний, пропускаемых звеном без заметного ослабления.


 ;
;  ;
;  ;
; 

 (3.13) иногда пишут
(3.13) иногда пишут 

 argW(j
argW(j 


 ????
????


 <1 - коэффициент демпфирования звена (или коэффициент затухания).
<1 - коэффициент демпфирования звена (или коэффициент затухания).








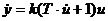



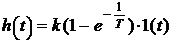
 Затухающие гармонические
колебания
Затухающие гармонические
колебания









 , где h(t)-максимальное значение на графике.
, где h(t)-максимальное значение на графике. * Модуль звена постоянного запаздывания определяются выражением:
* Модуль звена постоянного запаздывания определяются выражением: *Для звена
*Для звена  (идеальное интегрирующее) частотная передаточная функция имеет вид
(идеальное интегрирующее) частотная передаточная функция имеет вид  *Для звена
*Для звена 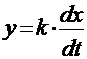 (дифференцирующее) частотная передаточная функция имеет вид
(дифференцирующее) частотная передаточная функция имеет вид 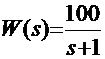 (апериодическое) АФЧХ имеет вид:
(апериодическое) АФЧХ имеет вид: 



 - свободная составляющая выходной величины системы.
- свободная составляющая выходной величины системы. .
. то система неустойчива.
то система неустойчива. . В этом случае говорят, что система находится на колебательной границе устойчивости.
. В этом случае говорят, что система находится на колебательной границе устойчивости.