
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные задачи динамики материальной точки.Цель работы: знакомство с двумя основными задачами динамики материальной точки.
Задача Д1:вычислить и построить траекторию движения материальной точки массой 1 кг под действием силы
Указания:задача Д1 на интегрирование дифференциальных уравнений движения точки. Решение задачи имеет следующие этапы: составление дифференциальных уравнений, вычисление общего интеграла, нахождение закона движения материальной точки с использованием начальных условий, определение траектории точки, построение траектории точки на чертеже.
Пример Д1:вычислить и построить траекторию движения материальной точки массой 1 кг под действием силы F, проекции которой на оси
Решение: 1. По второму закону Ньютона проекция силы на 
2. По второму закону Ньютона проекция силы на Интегрируя это дифференциальное уравнение, получим:
3. Таком образом, уравнение движения материальной точки Для получения траектории следует из данных уравнений исключить параметр t:
4. Построим данную кривую: Y
M0
0 X Ответ:
Лабораторная работа №4. Колебательное движение материальной точки. Цель работы:приобретение теоретических знаний о колебательном движении материальной точки над действием силы, пропорциональной расстоянию.
Задача Д2:груз массой m присоединили к концу недеформированной пружины и отпустили без начальной скорости, в результате чего он стал совершать колебательные движения. При статическом равновесии длина пружины изменилась на 1. Уравнение движения груза 2. Амплитуду и период колебания Трением и массой пружины пренебречь.
Таблица Д2. Последняя цифра зачетной книжки
Указания:задача Д2 относится к колебанию материальной точки. Для его решения необходимо: составить дифференциальное уравнение 2-го порядка, проинтегрировать данное уравнение, учтя начальные условия.
Предпоследняя цифра зачетной книжки
Пример Д2:груз массой 1 кг присоединили к концу недеформированной пружины и отпустили без начальной скорости, в результате чего он стал совершать колебательные движения. При статическом равновесии пружина удлинилась на 10 см. определить: 1. Уравнение движения груза; 2. Амплитуду и период колебания; Трением и массой пружины пренебречь. Решение: Отметим на рисунке Д2 положения: недеформированной пружины (1), груза, в котором он остановится при статическом равновесии (2),груза в произвольный момент времени. Направим ось
s w:space="720"/></w:sectPr></w:body></w:wordDocument>">
0
X
На груз действуют силы: s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> В этом уравнении нам известен параметр С. Чтобы его найти, рассмотрим груз в положении статического равновесия ( Подставляя значения С, m, P в наше дифференциальное уравнение движения груза, получим: Общее решение данного уравнения имеет вид
Где С1 и С2 постоянные интегрирования. Для вычисления С1 и С2 найдем
Таким образом, уравнение движения груза имеет вид Амплитуда колебания
Период колебания T найдем по формуле Ответ:
Лабораторная работа№5. Силы трения скольжения. Цель работы:учет влияния сил трения скольжения на работу простейших механизмов.
Задача Д3:три груза m1, m3, m5 связаны нитью, которая без проскальзывания идет через подвижные блоки массой m2 и m4. Определить ускорение грузов, считая нить нерастяжимой и невесомой, блоки – однородными дисками. Коэффициент трения грузов о поверхность равен
Указания: задача Д3 – на применение 2-го закона Ньютона для поступательного и вращательного движения.
Пример Д3:три груза m1=5 кг, m3=10 кг, m5=10 кг связаны нитью, которая без проскальзывания идет через подвижные блоки m2=2 кг, m4=2 кг. Определить ускорение грузов, считая движение равнопеременным, нить нерастяжимой и невесомой, блоки – однородными дисками. Коэффициент трения грузов о поверхность равен 0.20.
Предпоследняя цифра зачетной книжки
Таблица Д3. Последняя цифра зачетной книжки

m1
m5
Рис. Д3.
Решение: отметим на рис. Д3 положение грузов в произвольный момент времени. Предположим, что грузы будут перемещаться вправо. Обозначим все силы, действующие на грузы: сила тяжести, нормальная реакция опоры, сила натяжения нити и сила трения. Ускорение всех грузов обозначим через Рассмотрим движение каждого груза отдельно. На груз m1 действуют силы:
Преобразуя которые, получим:
Для груза m3 справедлива система уравнений:
Преобразуя которые, получим:
Для груза m5 справедливо равенство:
Для блока 2 можно записать
Отсюда Аналогично рассуждая, для блока 4 получим: Сложив уравнения 1, 2, 3, запишем:
Используя уравнения 4, 5 сделаем следующие преобразования:
Откуда выразим ускорения грузов
Ответ:
Статика.
Лабораторная работа №6. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 403. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , проекции которых на оси
, проекции которых на оси  и
и  и начальные условия представлены в табл. Д1.1 и Д1.2.
и начальные условия представлены в табл. Д1.1 и Д1.2. и
и  (H), используя начальные условия: М0 (1;4), V0=
(H), используя начальные условия: М0 (1;4), V0=  .
. ,
, 




 ,
, 









 по времени
по времени  ; т. к.
; т. к.  =1кг, имеем
=1кг, имеем  . Интегрируя это дифференциальное уравнение, получим
. Интегрируя это дифференциальное уравнение, получим  , где
, где  и
и  - постоянные интегрирования. Подставив начальные условия (
- постоянные интегрирования. Подставив начальные условия ( 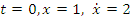 ) в данные уравнения, найдем
) в данные уравнения, найдем  .
. т. е.
т. е.  .
. , где
, где  ) в данные уравнения, найдем
) в данные уравнения, найдем  .
. .
. .
.
 .
. . Определить, используя данные в таблице Д2 и на рис. Д2.0-Д2.9:
. Определить, используя данные в таблице Д2 и на рис. Д2.0-Д2.9: Y
Y

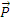 – сила тяжести, s w:space="720"/></w:sectPr></w:body></w:wordDocument>">
– сила тяжести, s w:space="720"/></w:sectPr></w:body></w:wordDocument>">  – нормальная реакция опоры,
– нормальная реакция опоры,  , где
, где  , C – коэффициент жесткости пружины,
, C – коэффициент жесткости пружины, 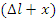 – удлинение пружины. Таким образом, уравнение движения примет вид
– удлинение пружины. Таким образом, уравнение движения примет вид ;
; .
. ):
):  , откуда
, откуда .
. . Это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Решается с помощью соответствующего характеристического уравнения:
. Это линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Решается с помощью соответствующего характеристического уравнения:  .
.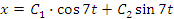 ,
, и используем начальные условия
и используем начальные условия 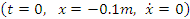
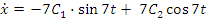 ,
, .
.

 – период косинуса:
– период косинуса: 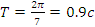
 ;
;  .
. .
.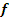

 m3
m3

 45° 30° m4
45° 30° m4



 .
. . Для него справедлива следующая система:
. Для него справедлива следующая система:
 (1)
(1)
 (2)
(2)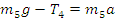 (3)
(3) , где
, где  – момент инерции блока 2,
– момент инерции блока 2,  - его угловое ускорение,
- его угловое ускорение,  - момент сил, вращающих блок 2.
- момент сил, вращающих блок 2.
 (4)
(4) (5)
(5) .
. .
.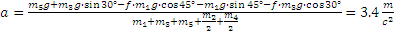 .
. .
.