
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Находят точечные оценки параметров нормального распределения СВ.Правила определения оценок для параметров нормального распределения по совокупности независимых измерений СВ регламентируются ГОСТ 11.004 ‑ 74. Наиболее достоверной оценкой измаеряемой СВ является ее СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ИЛИ СРЕДНЕЕ ВЗВЕШАННОЕ ЗНАЧЕНИЕ. Среднее арифметическое значение определяется тогда, когда все варианты (значения СВ) имеют одну и ту же частоту, равную единице (нет одинаковых значений СВ), что характерно для малых выборок. Если варианты имеют различные частоты, что характерно для больших выборок, то рассчитывают среднее взвешанное значение СВ по следующей формуле:
где: Ø Ø mi– частота (число вариантов СВ), соответствующаяi‑ му интервалу; Ø k – число интервалов. Наряду со средним взвешенным значением СВ в качестве характеристик вариационного ряда, дающих информацию о законе распределения, используют МЕДИАНУ И МОДУ. Медиана (m0,5) – это значение СВ, которое делит вариационный ряд или площадь, ограниченную кривой распределения, на две равные части. При нечетном объеме выборки медиана равна
а при четном объеме
где: xm – значение средней по порядку вариационного ряда случайной величины. (Например, если в вариационном ряду 51 значение случайной величины, то m0,5 будет равна значению 26, если 50 – то 25) Модой m0 называют варианту, которая имеет наибольшую частоту, т.е. соответствует вершине распределения (это наиболее вероятное значение случайной величины).  Оценивают моду по следующей формуле
где:
наибольшую частоту; h – длина интервала разбиения (шаг);
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 304. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
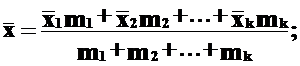 (5)
(5)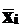 - значение варианта (СВ) в середине i ‑го интервала вариационного ряда;
- значение варианта (СВ) в середине i ‑го интервала вариационного ряда; , (6)
, (6)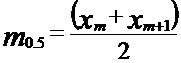 , (7)
, (7)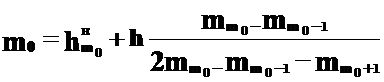 , (8)
, (8)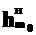 - нижняя граница модального интервала, т.е. интервала, имеющего
- нижняя граница модального интервала, т.е. интервала, имеющего 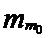 - частота модального интервала;
- частота модального интервала;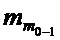 - частота интервала, предшествующего модальному интервалу;
- частота интервала, предшествующего модальному интервалу;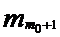 - частота интервала, следующего за модальным интервалом.
- частота интервала, следующего за модальным интервалом.