
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Раздел 4. Частотный метод Попова при отключенной местной обратной связи
В режиме стабилизации температуры можно принять Коэффициент усиления линейной части системы равен Коэффициент усиления нелинейного звена системы равен Коэффициент усиления линейной части системы и нелинейного звена Необходимо определить, при каких значениях kсистема будет абсолютно устойчива, если характеристика нелинейного звена расположена в секторе (0, k) Частотная передаточная функция линейной части системы имеет вид:
Её вещественная и мнимая части соответственно равны:
Введем некоторые функции
По данным выражениям построим характеристику Уравнение прямой Попова, коэффициенты которого получены путем подбора, приведено ниже:
Рис. 2. Характеристика V*(ω)=ƒ(U*(ω)) и прямая Попова
Система абсолютна устойчива для всех нелинейных характеристик, лежащих в секторе 0<k<1,5 и, в частности, для характеристики релейного типа.
Раздел 5. Алгебраический метод По структурно-математической схеме определяем дифференциальное уравнение линейной части системы при отключенной местной обратной связи и
Для линейного звена запишем гармонически линеаризованное выражение:
где для нелинейности
Подставляя значение u из уравнения (5.2) в уравнение (5.1), получим линеаризованное уравнение замкнутой нелинейной системы
где Этому дифференциальному уравнению соответствует характеристическое уравнение
Условие существования в уравнении (5.4) периодического решения
Будем отыскивать с помощью критерия Михайлова. Для этого в характеристический полином
Подставим
Из второго уравнения системы (5.8) найдем искомую частоту периодического решения Подставим это решение в первое уравнение (5.8) и найдем выражение, связывающее амплитуду периодического решения a=A с параметрами системы:
Отсюда получим: Для исследования устойчивости найденного периодического решения воспользуемся приближенным аналитическим условием, согласно которому периодическое решение устойчиво, если выполняется неравенство:
Из выражений (5.8) находим
Подставим выражения для частных производных в (5.10) и одновременно произведем замену Получим условие устойчивости периодического решения в виде
В данном случае условие существования периодического решения имеет вид:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 269. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.
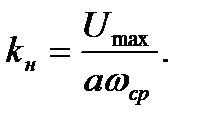
 условно отнесем к нелинейному звену.
условно отнесем к нелинейному звену. (4.1)
(4.1) (4.2)
(4.2) следующим образом:
следующим образом: (4.3)
(4.3)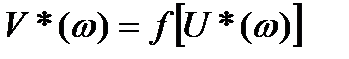 и через точку (-1/k, j0) проведем прямую Попова так, чтобы построенная характеристика целиком лежала справа от этой прямой.
и через точку (-1/k, j0) проведем прямую Попова так, чтобы построенная характеристика целиком лежала справа от этой прямой.
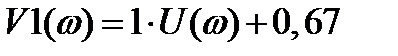





 :
: (5.1)
(5.1) (5.2)
(5.2) (5.3)
(5.3) (5.4)
(5.4) - коэффициент усиления линейной части системы.
- коэффициент усиления линейной части системы. (5.5)
(5.5) (5.6)
(5.6) (5.7)
(5.7) , выделим вещественную и мнимую части и приравняем их нулю:
, выделим вещественную и мнимую части и приравняем их нулю: (5.8)
(5.8)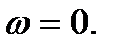
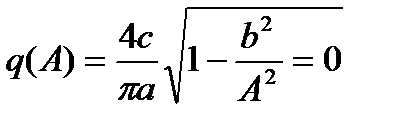 (5.9)
(5.9)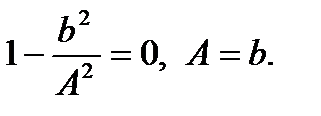
 (5.10)
(5.10)
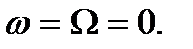
 (5.11)
(5.11) Следовательно, автоколебания отсутствуют, состояние равновесия системы устойчиво.
Следовательно, автоколебания отсутствуют, состояние равновесия системы устойчиво.