
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Раздел 2. Метод фазовых траекторийСтр 1 из 3Следующая ⇒ Введение Успешное решение задач автоматизации в настоящее время тесным образом связано с использованием современных технологий теоретических и практических разработок автоматических систем управления. Синтез структуры и определение параметров управляющего устройства выполняются в определенной последовательности по классической схеме. Вначале исследуются свойства управляемого объекта по его характеристикам. Структура и параметры объекта при этом считаются известными, процессы в объекте описываются нелинейными дифференциальными уравнениями. Нелинейность объекта вызвана нелинейностью одного из устройств с типовой нелинейной характеристикой. Определение требуемой структуры управляющего устройства ведется путем итераций от самых простых решений до сложных структур на основе требований технического задания. Из теории линейных систем известно, что монотонный характер переходной характеристики можно получить при плохом быстродействии системы управления. . Для исследования релейных систем высокого порядка на фазовой плоскости используется редуцирование или понижение порядка дифференциального уравнения. Из известных методов редуцирования приводится один, а именно, редуцирование путем приведения исходной системы к каноническому виду. Раздел 1. Основные сведения Решение задачи для следующих исходных данных: -постоянная времени объекта -коэффициент усиления объекта и регулирующего органа k0 =10 град/рад, -коэффициент усиления чувствительного элемента k1=0,3 А-в/град, - коэффициент усиления двигателя k2=2 рад/(В*с), -передаточное отношение редуктора i=800,  - коэффициент усиления цепи обратной связи kос=2,5 А-в/рад, -ампер-витки срабатывания реле -максимальное напряжение на выходе релейного усилителя Umax=100 В. Описание САУ Составление уравнений элементов САУ. Для заданной принципиальной схемы составим дифференциальные уравнения звеньев системы. Уравнение регулируемого объекта
где Уравнение чувствительного элемента.
где Уравнение релейного усилителя.
где Уравнение двигателя постоянного тока.
где Уравнение редуктора.
где Уравнение цепи обратной связи
где Составление структурно-математической схемы САУ Структурно-математическая схемы системы автоматического регулирования температуры изображена на рис.3. В соответствии со структурно – математической схемой дифференциальное уравнение линейной части системы можно записать в следующем виде: Подставим в уравнение (1.7) численные значения параметров и получим Уравнение нелинейной части (1.7) дополняется уравнением нелинейного звена (1.3) Раздел 2. Метод фазовых траекторий Исследуем устойчивость САУ температуры методом фазового пространства при отключенной местной обратной связи (см. рис.1). В режиме стабилизации температуры можно принять 1) Уравнение объекта регулирования 2) Уравнение чувствительного элемента 3) Уравнение усилителя (при kос=0) 4) Уравнение двигателя постоянного тока 5) Уравнение редуктора
Учитывая, что ток в обмотке поляризованного реле пропорционален отклонению температуры
Рис. 1. Статическая характеристика нелинейного звена На этом рисунке
В соответствии с уравнением объекта регулирования (2.1) и статической характеристикой нелинейого звена (см.рис. 1) уравнения всей системы можно записать в следующем виде:
(2.7)
(2.8) (2.9) (2.10)
(2.11)
(2.12)
(2.13)
(2.14)
(2.15)
(2.16)
Подставив в уравнения (2.14) - (2.16) численные значения, получим:
По данным уравнениям построим фазовый портрет всей системы. Раздел 3. Метод Ляпунова
Согласно структурно-математической схеме САУ температуры описывается следующими дифференциальными и алгебраическими уравнениями:
(3.1)
Введем обозначения:
Получим:
Общий вид системы нелинейных уравнений 2-го порядка, заданных в нормальной форме, представлен ниже:
Откуда следует:
Запишем уравнения в канонической форме. Для этого из коэффициентов уравнения составим определитель.
Для нашего случая определитель имеет вид:
Определим корни характеристического уравнения
Ввиду того, что в характеристическом уравнении имеется один нулевой корень, канонические уравнения записываются в следующем виде:
Определим постоянные
где Dik(λ) обозначает алгебраическое дополнение элемента i - той строки и k-го столбца определителя D(λ).
По формуле (3.7) определим:
Определим D(λ):
Поскольку λ1=0, то и
Для класса нелинейных систем, к которому принадлежит рассматриваемая система, достаточные условия устойчивости имеют вид:
Это условие приводит к следующему достаточному условию устойчивости рассматриваемой системы:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 224. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 =0,5 с,
=0,5 с, =0,5,
=0,5,
 (1.1)
(1.1)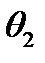 – фактическое значение температуры объекта,
– фактическое значение температуры объекта,  – угол поворота регулирующего органа.
– угол поворота регулирующего органа. (1.2)
(1.2) – заданное значение температуры объекта,
– заданное значение температуры объекта,  - ошибка рассогласования системы.
- ошибка рассогласования системы. (1.3)
(1.3) – нелинейная функция, заданная статической характеристикой (см.рис.2).
– нелинейная функция, заданная статической характеристикой (см.рис.2). (1.4)
(1.4) - угол поворота вала двигателя.
- угол поворота вала двигателя. (1.5)
(1.5)  - коэффициент передачи редуктора.
- коэффициент передачи редуктора. (1.6)
(1.6) - ампер-витки обмотки обратной связи.
- ампер-витки обмотки обратной связи. (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9) . При этом уравнения звеньев системы можно записать в следующем виде:
. При этом уравнения звеньев системы можно записать в следующем виде:


 , а скорость отклонения регулирующего органа
, а скорость отклонения регулирующего органа 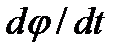 пропорциональна напряжению
пропорциональна напряжению 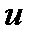 , в качестве входной величины нелинейного звена (поляризованного реле) можно принять
, в качестве входной величины нелинейного звена (поляризованного реле) можно принять 

 (2.6)
(2.6)


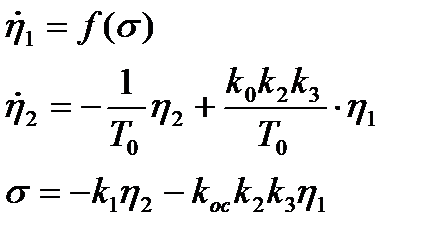 (3.2)
(3.2) (3.3)
(3.3)
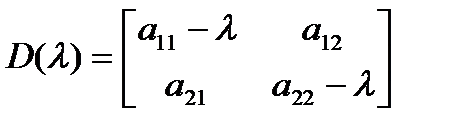 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) :
:  (3.7)
(3.7)
 (3.8)
(3.8)
 (3.9)
(3.9)
