
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение дисперсии воспроизводимости.Прежде чем переходить к планированию эксперимента для исследования какого-либо технологического объекта, необходимо определить воспроизводимость процесса на данной технологической установке. Под воспроизводимостью процесса понимают независимость результатов эксперимента от времени; оценивается она величиной дисперсии воспроизводимости Дисперсия воспроизводимости является важным статистическим показателем характеризующий уровень «шума» на установке. Уровень шума «шума» зависит от погрешностей измерения выходного и входных параметров, от степени влияния неучтенных, неуправляемых факторов и т.д. Дисперсия воспроизводимости используется при статистическом анализе значимости рассчитанных оценок коэффициентов и при проверке адекватности полученных уравнений. Так как основным рабочим методом обработки наблюдений при планировании эксперимента является регрессивный анализ (одной из предпосылок которого является требование постоянства величины 
где, yi – результат наблюдений в параллельных опытах (i=1,2,…,r);
fo=r-1- число степеней свободы , связанное с дисперсией воспроизодимости. Если у исследователей нет уверенности в однородности дисперсии
где,
Затем вычисляется суммарная дисперсия:
где m – число серий. Однородность дисперсий определяется по критерию Кохрана, для чего вычисляется расчетное значение этого критерия:
Расчетное значение критерия сравнивается с табличным при к1=r-1 (число степеней свободы для числителей) и к2=m – число сравниваемых дисперсий. Если Gp не превышает критическую, дисперсии однородны и процесс воспроизводим. Оценкой дисперсии воспроизводимости в данном случае является среднее арифметическое из всех дисперсий:
Число степеней свободы для дисперсии воспроизводимости:
Средняя квадратичная ошибка опыт а:
Если число параллельных наблюдений в сериях неодинаково, то для сравнения дисперсий применяют критерий Бартлета, а величину дисперсии воспроизводимости определяют по формуле:
В данном случае число степеней свободы:
Если дисперсии неоднородны положение существенно усложняется, так как нарушена основная предпосылка регрессионного анализа, вследствие этого чего не может быть применен. В этом случае полезно найти такое преобразование параметра оптимизации. которое позволило бы получить нормальное или близкое к нему распределение параметра. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , или
, или  , которая характеризует средний разброс результатов измерений выходного параметра в том случае, когда все влияющие факторы зафиксированы на каком-либо определенном уровне. Величину s0 называют ошибкой опыта. Если дисперсия воспроизводимости велика, применение методов планирования эксперимента будет неэффективна.
, которая характеризует средний разброс результатов измерений выходного параметра в том случае, когда все влияющие факторы зафиксированы на каком-либо определенном уровне. Величину s0 называют ошибкой опыта. Если дисперсия воспроизводимости велика, применение методов планирования эксперимента будет неэффективна. (1.26)
(1.26) – среднее значение параметра y и r параллельных опытах;
– среднее значение параметра y и r параллельных опытах; (1.27)
(1.27) - среднее значение выхода j-той серии опытов;
- среднее значение выхода j-той серии опытов; (1.28)
(1.28)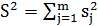 (1.29)
(1.29) (1.30)
(1.30)  (1.31)
(1.31) (1.32)
(1.32) (1.33)
(1.33) (1.34)
(1.34) (1.35)
(1.35)