
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Общая характеристика прямых методов решения СЛАУ.Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида (1)
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1]. Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной. Система (1) называется квадратной, если число m уравнений равно числу n неизвестных. Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Совместная система вида (1) может иметь одно или более решений. Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой. Матричная форма Система линейных уравнений может быть представлена в матричной форме как:
Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. Прямые (или точные) методы, позволяют найти решение за определённое количество шагов. Итерационные методы, основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.  7.Теорема об LU-разложении. LU-разложение — представление матрицы A в виде LU, где L — нижняя треугольная матрица с диагональными элементами, равными единице, а U — верхняя треугольная матрица. LU-разложение еще называют LU-факторизацией. Алгоритм LU-разложения лежит в основе широко распространённого метода решения систем линейных алгебраических уравнений (СЛАУ) — метода Гаусса. Матрица L является нижнетреугольной, с единичной диагональю, поэтому её определитель равен 1. Матрица U — верхнетреугольная матрица, значит её определитель равен произведению элементов, расположенных на главной диагонали. Будем использовать следующие обозначения для элементов матриц L = (lij), U = (uij), Найти матрицы L и U можно следующим образом (выполнять шаги следует строго по порядку, так как следующие элементы находятся с использованием предыдущих):
Для
В итоге мы получим матрицы — L и U. В программной реализации данного метода (компактная схема Гаусса) для представления матриц L и U можно обойтись всего одним массивом, в котором совмещаются матрицы L и U. Например, так (для матрицы размером
8.Метод Гаусса Метод Гаусса и его модификации основаны на приведении с помощью элементарных преобразований исходной системы к системе верхней треугольной или диагональной матрицы. В схеме единственного деления на каждом шаге строка делится на элемент, стоящий на главной диагонали (ведущий элемент), и исключаются элементы под главной диагональю. Предположим, что
Подсчитаем число арифметических операций, необходимых для решения системы (4.1) по схеме единственного деления. Так как выполнение операций умножения и деления на ЭВМ требует гораздо больше времени, чем выполнение сложений и вычитаний, то подсчитаем только число умножений и делений. 1. Вычисление коэффициентов После преобразования исходной системы по схеме единственного деления получаем систему вида
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 482. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 или:Ax = B.
или:Ax = B.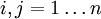 ; причём диагональные элементы матрицы L: lii = 1,
; причём диагональные элементы матрицы L: lii = 1,  . Тогда, если известно LU-разложение матрицы, её определитель можно вычислить по формуле det(A) = det(LU) = det(L)det(U) = det(U) = произведению элементов на диагонали матрицы U.
. Тогда, если известно LU-разложение матрицы, её определитель можно вычислить по формуле det(A) = det(LU) = det(L)det(U) = det(U) = произведению элементов на диагонали матрицы U.




 ):
):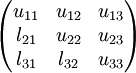
 ,
,  и
и  шагов метода уже сделаны. Тогда на
шагов метода уже сделаны. Тогда на  -ом шаге расчетные формулы имеют вид
-ом шаге расчетные формулы имеют вид ,
,  , (4.3)
, (4.3)  , (4.4)
, (4.4) 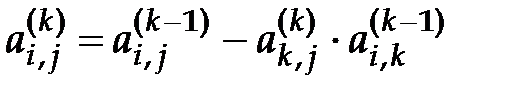 , (4.5)
, (4.5)  ,
,  . (4.6) После
. (4.6) После  -го шага матрица системы принимает вид
-го шага матрица системы принимает вид  . (4.7) Процесс приведения матрицы исходной системы к системе с верхней диагональной матрицей называется прямым ходом метода Гаусса, а процесс получения значений неизвестных – обратным ходом. Неизвестные из преобразованной системы находятся по формулам
. (4.7) Процесс приведения матрицы исходной системы к системе с верхней диагональной матрицей называется прямым ходом метода Гаусса, а процесс получения значений неизвестных – обратным ходом. Неизвестные из преобразованной системы находятся по формулам ,
,  ,
, 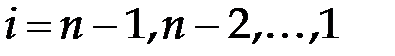 . (4.8)
. (4.8)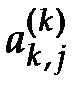 ,
,  ,
,  по формулам (4.3) требует
по формулам (4.3) требует  делений. 2. Вычисление всех коэффициентов
делений. 2. Вычисление всех коэффициентов 
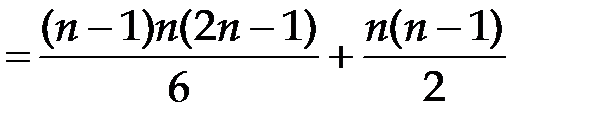 умножений. Таким образом, вычисление элементов верхней треугольной матрицы требует
умножений. Таким образом, вычисление элементов верхней треугольной матрицы требует  операций умножения и деления. 3. Вычисление правых частей по формулам (4.4) требует
операций умножения и деления. 3. Вычисление правых частей по формулам (4.4) требует  по формулам (6)
по формулам (6)  умножений. Следовательно, для вычисления правых частей необходимо
умножений. Следовательно, для вычисления правых частей необходимо  операций умножения и деления. В итоге для осуществления прямого хода метода Гаусса необходимо выполнить
операций умножения и деления. В итоге для осуществления прямого хода метода Гаусса необходимо выполнить  действий. 4. Для осуществления обратного хода метода Гаусса по формулам (4.8) необходимо выполнить
действий. 4. Для осуществления обратного хода метода Гаусса по формулам (4.8) необходимо выполнить  умножений. Окончательно получаем, что для реализации схемы единственного деления метода Гаусса необходимо выполнить
умножений. Окончательно получаем, что для реализации схемы единственного деления метода Гаусса необходимо выполнить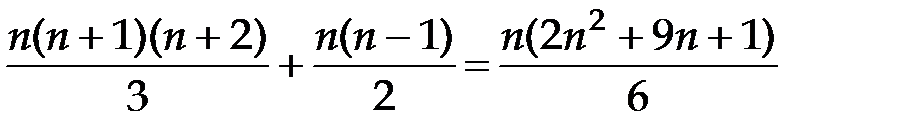 операций умножения и деления.
операций умножения и деления. , где матрица
, где матрица  это матрица (4.7). Подставляя в (4.1) выражение для
это матрица (4.7). Подставляя в (4.1) выражение для 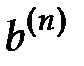 в виде
в виде  приходим к уравнению
приходим к уравнению  или, что то же самое, к уравнению
или, что то же самое, к уравнению  . Сопоставляя последнею систему с системой (4.1) приходим к выводу, что при применении метода Гаусса матрица
. Сопоставляя последнею систему с системой (4.1) приходим к выводу, что при применении метода Гаусса матрица  системы есть произведение нижней треугольной матрицы
системы есть произведение нижней треугольной матрицы  на верхнюю треугольную матрицу
на верхнюю треугольную матрицу  .
.