
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Погрешности приближенных вычисленийСтр 1 из 4Следующая ⇒ Устойчивость решения СЛАУ. Решение системы Ax=b задается формулой Пусть При решении задач на практике часто бывает трудно оценить число обусловленности матрицы А. Поэтому существует ряд приемов, которые хотя и не дают строгий ответ об устойчивости применяемого метода и полученного решения, но все же позволяют сделать некоторые предположения о характере решения. Уточнить полученное решение и оценить его погрешность можно осуществить следующим образом. Пусть получено приближенное решение системы (1)
отсюда
Можно видеть, что для нахождения поправки можно использовать алгоритм метода и соответствующую программу, по которой находилось основное решение. После этого можно уточнить решение системы 
3. Математическое моделирование. Построение мат модели системы Математическое моделирование основывается на известном факте: различные изучаемые процессы могут иметь одинаковое математическое описание. Следовательно, если система определена и ее функция может быть описана с помощью математических и логических предложений, то исследование системы возможно математическими средствами и средствами вычислительной техники. Математическая модель концентрирует в себе записанную в форме математических предложений совокупность наших знаний, представлений и гипотез о соответствующем объекте, процессе, явлении или системе. Поскольку эти знания никогда не бывают абсолютными, то можно утверждать, что математическая модель только с определенной достоверностью описывает поведение реальной системы. Поэтому при построении математических моделей систем необходимо учитывать следующие основные требования: адекватность, универсальность, точность и экономичность. · Адекватность. Математическая модель считается адекватной исходной системе, если она отражает заданные её свойства с допустимой точностью. Пусть модель имеет k выходных параметров, тогда погрешность модели εмод можно представить как норму вектора ε = { ε1, ε2, …, εk }; εмод = max | εj |, j = - относительная погрешность модели по j-у выходному параметру, yje, yj - вычисленное и действительное значение j-го выходного параметра. Должно выполнятся условие εмод < εпред , где εпред - предельная допустимая погрешность. Область в пространстве внешних параметров, для которой выполняется это условие, называется областью адекватности модели. · Универсальность. Это характеристика полноты отображения в модели исследуемых свойств реальной системы. · Точность. Оценивается точность математической модели степенью совпадения значений параметров исходной системы и значений тех же параметров, вычисленных с помощью оцениваемой математической модели. Погрешности математического моделирования определяются двумя факторами: степенью точности формального описания исходной системы и точностью определения исходных данных. · Экономичность. Эта характеристика стоимости исследования модели системы по разработанному алгоритму на компьютере. Основное назначение математического моделирования - сделать возможными некоторые выводы о поведении реальной системы в пространстве и времени. Для построения математических моделей используют различные методы, которые можно объединить в две группы: формальные и неформальные методы. Формальные методы применяют для построения математических моделей систем при известных математических моделях элементов. Неформальные методы применяются для синтеза теоретических и эмпирических математических моделей. Теоретические математические модели создаются в результате исследования процессов и их закономерностей, присущих рассматриваемому классу систем. Эмпирические математические модели создаются в результате изучения внешних проявлений свойств системы. Математическая модель сложной системы получается как синтез математических моделей её элементов. Полученная совокупность моделей повторит структуру и иерархию самой системы. Отметим, что основной спецификой моделирования систем является учёт связей между отдельными моделями. Математическая модель это некоторый абстрактный образ, т.е. конечная совокупность логико-математических предложений, адекватно отражающих основные закономерности и особенности оригинала, т.е. реального объекта или системы, которые имеют свою среду (пространство) и условия существования. Всякая реальная система или объект всегда имеют определенные связи с внешней средой, которая налагает свои условия на их существование и функционирование В самом общем случае эта структурная схема автором представлена следующим образом:Математическая модель среды существования системы,Математическая модель состояния среды системы или объекта, Условия связи системы с внешней средой, Математическая модель основной функции системы,Математическая модель результата решения. Математическое наполнение элементов этой структуры зависит от класса моделируемых задач и даже от особенностей задач одного класса. Известно, что наиболее трудным этапом системных исследований является построение и оценка адекватности математической модели реальной системе. Предлагаемая структурная схема является общим эффективным алгоритмом построения математических моделей систем или объектов. Таким образом, в процессе математического моделирования исследователь имеет дело с тремя объектами: 1. с системой (реальной, проектируемой, воображаемой), 2. с математической моделью системы, 3. с алгоритмической (машинной) моделью. В соответствии с этим возникают следующие задачи: 1. определение и формирование системы, 2. построение математической модели системы, 3. разработка метода исследования математической модели, 4. разработка программного комплекса. Процесс моделирования содержит определённые этапы. Погрешности приближенных вычислений Ошибкой или погрешностью приближенного числа a называется разность между точным и приближенным значениями Все сохраняемые в представлении числа цифры Теорема1. Если положительное число где
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 487. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Влияние ошибок округления может привести к тому, что в процессе счета будет получена система уравнений, не равносильная исходной. Возникает вопрос об устойчивости метода решения.
. Влияние ошибок округления может привести к тому, что в процессе счета будет получена система уравнений, не равносильная исходной. Возникает вопрос об устойчивости метода решения. и
и  - заданные величины, а
- заданные величины, а  и
и  - близкие к ним. Будем рассматривать
- близкие к ним. Будем рассматривать  ,
,  и
и 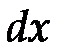 как дифференциалы. Тогда из формулы Ax=b имеем
как дифференциалы. Тогда из формулы Ax=b имеем  . Откуда
. Откуда  . Отсюда следует, что если элементы обратной матрицы велики, то незначительная ошибка в элементах исходной матрицы или правой части может повлечь за собой значительное изменение в решении. Поэтому при выборе метода решения системы нужно обращать внимание на условия его устойчивости.
. Отсюда следует, что если элементы обратной матрицы велики, то незначительная ошибка в элементах исходной матрицы или правой части может повлечь за собой значительное изменение в решении. Поэтому при выборе метода решения системы нужно обращать внимание на условия его устойчивости. . Вычислим невязку уравнения
. Вычислим невязку уравнения  . Если
. Если  велико, то можно искать вектор-поправку
велико, то можно искать вектор-поправку  такой, что точное решение системы
такой, что точное решение системы  . Следовательно
. Следовательно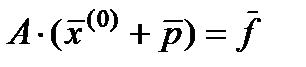 ,
, .
. . Если относительная погрешность
. Если относительная погрешность  велика, то можно повторить процесс уточнения. Если процесс уточнения, повторенный два три раза, не приводит к повышению точности, то это говорит скорей всего о том, что данная система плохо обусловлена и ее решение не может быть найдено с требуемой точностью.
велика, то можно повторить процесс уточнения. Если процесс уточнения, повторенный два три раза, не приводит к повышению точности, то это говорит скорей всего о том, что данная система плохо обусловлена и ее решение не может быть найдено с требуемой точностью. ; или
; или  εмод =
εмод = 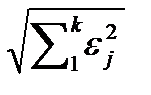 , где
, где 
 . Величина
. Величина  называется абсолютной погрешностью. Отношение абсолютной погрешности к модулю точного значения
называется абсолютной погрешностью. Отношение абсолютной погрешности к модулю точного значения 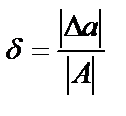 (1.1)называется относительной погрешностью числа
(1.1)называется относительной погрешностью числа  . Таким образом абсолютная и относительная погрешности связаны формулой
. Таким образом абсолютная и относительная погрешности связаны формулой  .(1.2) Так как точное значение
.(1.2) Так как точное значение  как правило неизвестно, то при достаточно малой абсолютной погрешности можно считать, что
как правило неизвестно, то при достаточно малой абсолютной погрешности можно считать, что  . Абсолютная погрешность является мерой ошибки числа
. Абсолютная погрешность является мерой ошибки числа  , а относительная погрешность определяет меру точности приближенного числа. На практике, как правило, известны лишь границы абсолютной и относительной точности приближенного числа. Любое число
, а относительная погрешность определяет меру точности приближенного числа. На практике, как правило, известны лишь границы абсолютной и относительной точности приближенного числа. Любое число  такое, что
такое, что  , называется предельной абсолютной погрешностью, а
, называется предельной абсолютной погрешностью, а  такое, что
такое, что  , - предельной относительной погрешностью. Пусть число
, - предельной относительной погрешностью. Пусть число  в позиционной системе с основанием 10 имеет вид
в позиционной системе с основанием 10 имеет вид  .
. называются значащими, за исключением нулей, которые служат лишь для обозначения разрядов. Первые
называются значащими, за исключением нулей, которые служат лишь для обозначения разрядов. Первые  значащих цифр приближенного числа являются верными в узком (широком) смысле, если абсолютная погрешность этого числа не превышает половины (единицы) разряда, выраженного
значащих цифр приближенного числа являются верными в узком (широком) смысле, если абсолютная погрешность этого числа не превышает половины (единицы) разряда, выраженного  -й значащей цифрой, отсчитываемой слева направо:
-й значащей цифрой, отсчитываемой слева направо:  или
или  . (1.3)
. (1.3) имеет
имеет 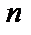 верных десятичных знаков в узком смысле, то относительная погрешность удовлетворяет неравенству
верных десятичных знаков в узком смысле, то относительная погрешность удовлетворяет неравенству  , (1.4)
, (1.4)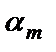 - первая значащая цифра числа
- первая значащая цифра числа  .Если
.Если  , то практически справедлива оценка
, то практически справедлива оценка  . (1.5) Формула (4) позволяет определить предельную относительную погрешность по количеству верных знаков. Если известно, что имеет место оценка
. (1.5) Формула (4) позволяет определить предельную относительную погрешность по количеству верных знаков. Если известно, что имеет место оценка 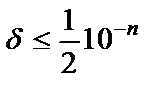 , то для абсолютной погрешности справедливо неравенство
, то для абсолютной погрешности справедливо неравенство  , т.е. число имеет, по крайней мере,
, т.е. число имеет, по крайней мере,  верных знаков.
верных знаков.