
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения пассивных четырёхполюсников с коэффициентами
Задача 5.1. Рассчитать ABCD–коэффициенты Г-схемы четырёхпо-люсника (рис. 5.4,а), если r = 10 Ом, xС = 10 Ом, xL = 20 Ом. Используя основные уравнения четырёхполюсника, определить входное сопротивление Z1ВХ при нагрузке Z2 = r2 = 20 Ом. Решение
I1 = С·U2 + D ×I2. При произвольной нагрузке в схеме рис. 5.4,а три неизвестных тока: I1, I2, IL. По первому закону Кирхгофа I1 = IL + I2, по второму закону Кирхгофа U2 – IL×jxL = 0, I1×(r – jxС ) + U2 = U1. Из этих уравнений получаем: I1 = I2 + откуда С = U1 = U2×(1 + откуда А = 1 + В = r – jxС = 10 – j10 = 10 Способ 2. Коэффициенты рассчитываются по уравнениям Кирхгофа для режимов холостого хода и короткого замыкания четырёхполюсника, когда основные уравнения принимают вид:
I1Х = С·U2Х ; I1К = D ·I2К . По схеме рис. 5.4,а, соответственно, получаем: I1Х = I1К = I2К = D ·I2К ; I1К ×(r – jxС) = U1К = В·I2К = I2К ×(r – jxС). Результаты расчёта коэффициентов совпали с ранее полученными. Способ 3. Расчёт коэффициентов осуществим по сопротивлениям холостого хода и короткого замыкания четырёхполюсника (рис. 5.4,а): Z1Х = r – jxС + jxL = 10 – j10 + j20 = 10 + j10 = 10  Z1К = r – jxС = 10 – j10 = 10 Z2Х = jxL = j20 = 20×е j·90° Ом; Z2К = Из основных уравнений для режимов холостого хода и короткого замыкания Z1Х = А/С, Z2Х = D/С, Z1К = В/D, Z2К = В/А. Выбирая любые три соотношения с учётом свойства коэффициентов А∙D – В∙С = 1, получаем сначала один из коэффициентов, а затем через выбранные три соотношения определяем остальные коэффициенты. Например, А = Комплексное число, стоящее в знаменателе, можно в показательной форме записать двояко: 1) j20 – 20 = 20 Соответственно, получаем 2 значения коэффициента А: А1 = Коэффициент А является в общем случае комплексным числом, которое в показательной форме имеет выражение А = а·е ja. Модуль коэффициента а = отрицательное a = a1= -45°, положительное a = a2= +135°. Отбор единственного значения a произведём на основании векторной диаграммы цепи (рис. 5.4,б) для режима холостого хода четырёхполюсника, когда U1Х = А·U2Х = а·е ja·U2Х . По векторной диаграмме получаем a < 0, тогда А = В = Z2К∙А = С = D = Z2Х∙С = 20·е j·90°(-j0,05) = 1. Входное сопротивление четырёхполюсника при произвольной нагрузке Z2 : Z1 =
х1 = 40 Ом, r2 = 10 Ом, r0 = х0 = 40 Ом. Используя основные уравнения четырёхполюс-ника в форме А, определить ток I1К на входе при закороченных выходных зажимах, если U1 = 100 В. Ответ: А = -j; В = -j50 Ом; С = 0,025 – j0,025 См; D = 1,25 – j0,25; I1К = 2,55 А.
Ответ: H11 = 7,69 + j1,54 Ом; H12 = -H21 = 0,231 – j0,15; H22 = -0,0231 – j0,00962 См; U1X = 50
Определить входное сопротивление ЛЭП Z при RНГ = 1000 Ом, СНГ = 10 мкФ. Ответ: A = D = 0,9885×е j0,53°; B = 148,3×е j59,80° Ом; C = 0,198∙10 -3×е j81,91° См; Z1П = Z2П = 10 4×е –j81,64° Ом; Z0П = 148,3×е j59,80° Ом; ZВХ = 986×е –j19,75° Ом.
U1 = -j50×I2 + 1,75×U2; I1 = 0,5×I2 – j0,0025×U2. Требуется получить Т-схему замещения четырёхполюсника, а также записать уравнения в Н-форме. Ответ: Z1T = j300 Ом, Z2T = -j200 Ом, Z0T = j400 Ом; H11= - j100 Ом, H12 = 2, H21 = -2, H22 = -j0,005 См.
Задача 5.6. Определить коэффициенты A, B, C, D несимметричного четырёхполюсника рис. 5.8,а, если хL = 80 Ом, хC = 40 Ом, r3 = r4 = 40 Ом.
Используя основные уравнения четырёхполюсника, рассчитать ток нагрузки I2, если сопротивление нагрузки Z2 = 60 + j30 Ом, а напряжение на входе U1 = 220 В. Решение Расчёт коэффициентов выполним с помощью входных сопротивлений. Z1Х = r4 + Z2Х = r4 + Z2К = = 20 – j33,33 = 38,87×e –j59,04° Ом. А = Получаем два главных значения коэффициента А = ае ja: А1 = 1,342×e –j26,57°; А2 = 1,342×e j153,43°. Отбор знака угла a осуществляем с помощью векторной диаграммы четырёхполюсника для режима холостого хода (рис. 5.8,б), из которой на основании основного уравнения U1X = А×U2X = аU2X е ja следует a < 0, то есть А = 1,342×e –j26,57° = 1,2 – j0,6. Далее В = Z2К ×А = 38,87×e –j59,04°×1,342×e –j26,57° = 52,16×e –j85,61° = 4 – j52 Ом, С = D = Первое основное уравнение U1 = А×U2 + B×I2 = А×I2×Z2 + B×I2, откуда I2 = действующее значение тока I2 = 2,05 А.
Задача 5.7. При экспериментальном исследовании четырёхполюсни-ка оказалось, что Z1Х = 1000 В режиме холостого хода сняты осциллограммы входного и выходного напряжений, приведенные на рис. 5.9,а. Требуется: 1. Определить коэффициенты A, B, C, D. 2. Рассчитать параметры П-схемы замещения четырёхполюсника и решить вопрос о её физической реализуемости. 3. Определить напряжение источника, ток и напряжение приёмника, если i1(t) = 20sin(wt + 90°) мА, а сопротивление приёмника Z2= 500 Ом. 4. Определить КПД четырёхполюсника. Решение
Найдём коэффициент А =  . .
Неизвестное сопротивление Z2К = Z2Х × а коэффициент А = Получаем два главных значения А1 = + Знак аргумента комплексного числа установим с помощью осциллограммы рис. 5.7,а, имея в виду, что в режиме холостого хода U1X = А×U2X и А = На приведенной осциллограмме Yu1X = 0, Yu2X = + таким образом, a = Yu1X –Yu2X = 0 – 45° = -45° и единственный для данного четырёхполюсника коэффициент А = + Отметим, что модуль коэффициента |А|= а также можно было опре-делить по осциллограмме: а =U1X m =U2X m. Однако точность определения величин по графикам низкая. Остальные коэффициенты В = Z2К ×А = 500 С = D = Параметры П-схемы замещения исследуемого четырёхполюсника: Z1П = Z2П = Z0П = В =1000 Ом – активное сопротивление. Все сопротивления схемы замещения, приведенной на рис. 5.9,б, физически реализуемы. Комплекс входного тока I1= I1×e jYi = Входное сопротивление четырёхполюсника вместе с нагрузкой Z1= Входное напряжение U1= I1×Z1= 10 -2 Из основного уравнения U1 = А×U2 + B×I2 = U2×(А + U2= По закону Ома I2= Активные мощности: - на входе четырёхполюсника P1= Re(U1× - на выходе четырёхполюсника P2= I22r2= (7,84×10 -3)2×500 = 30,73×10 -3 Bт. Коэффициент полезного действия h =
Задача 5.8. При переходе из воздушной линии в кабельную использована автотрансформаторная схема с конденсатором, приведенная на рис. 5.10,а. Параметры схемы: xС = 35 Ом, x1 = 20 Ом, x3 = 60 Ом, xМ =10 Ом. Определить коэффициенты А, В, С, D четырёхполюсника. При нагрузке Z2= r = 50 Ом её мощность Р2 = 450 Bт. Используя ос-новные уравнения, рассчитать активную мощность на входе. Решение Устраним индуктивную связь и получим эквивалентную Т-схему четырёхполюсника (рис. 5.10,б), у которого Z1 = -jхС + j(х1+хМ) = -j35 + j(20 + 10) = -j5 Ом, Z2 = -jхМ = -j10 Ом, Z0 = j(х2+хМ) = j(60 + 10) = j70 Ом. Для Т-схемы четырёхполюсника связь между коэффициентами и сопротивлениями установлена: A = 1 + B = Z1+ Z2+ C = D = 1 + Ток нагрузки I2= Примем I2= 3 А, по закону Ома U2= I2×Z2= 3×50 = 150 B. Далее U1= А×U2 + B×I2 = 0,928×150 + (-j15,7)×3 = 147×e –j18,7° B, I1= С×U2 + D×I2 = -j0,0143×150 + 0,857×3 = 3,35×e –j39,8° А, P1= Re(U1× Обратим внимание, что рассматриваемая схема четырёхполюсника яв-ляется схемой без потерь (без активных сопротивлений), для которой P1= P2. Расхождение в 9 Bт появилось вследствие округления результатов вычислений до трёх значащих цифр. При этом относительная погрешность вычислений по мощности составила e % =
ЗАДАЧА 5.9. Определить А-коэффициенты Х-схемы (мостовая схема) четырёхполюсника, пред-ставленного на рис. 5.11, если r = xL = xС = 10 Ом. Указание. При отборе единственного значения коэффициента А рекомендуется построить диаграмму комплексных потенциалов четырёхполюсника для режима холостого хода, приняв j 1¢ = 0. Ответы: А = 0,6 + j0,8, В = j20 Ом, С = 0,1 + j0,1 См, D = 1 + j2.
Задача 5.10. а) На зажимы источника переменного напряжения с ЭДС Е = 100 В и внутренним сопротивлением Zв = rв = 1 Ом подключена нагруз-ка Zн = rн = 9 Ом (рис. 5.12,а). Определить активную мощность приёмника Рн.
б) Для увеличения передаваемой в нагрузку активной мощности от генератора между генератором и нагрузкой включен четырёхполюсник (рис. 5.12,б). Определить параметры этого четырёхполюсника из условия передачи от генератора в нагрузку максимально возможной мощности Р2max. Решениезадания а). Ток в цепи рис. 5.12,а I = активная мощность приёмника Рн = I 2×rн = 10 2×9 = 900 Вт. Решениезадания б). Нагрузкой генератора в схеме рис. 5.12,б является четырёхполюсник, на выходные зажимы которого подключен приёмник, сопротивление которого Zн = rн = 9 Ом. Задачу передачи максимальной мощности от генератора через четырёхполюсник к приёмнику будем решать в два этапа: 1. Подберём такое сопротивление нагрузки на генератор Z1, при котором на вход четырёхполюсника поступит максимально возможная мощность Р1max. На основании основных уравнений четырёхполюсника при нагрузке Z2 = rн его входное сопротивление Z1 = Так как четырёхполюсник ещё требуется подобрать, то его коэффициенты можно принимать любыми, изменяя таким образом нагрузку на генератор. Заметим, что устройство, с помощью которого можно изменить (трансформировать) сопротивление нагрузки, называется трансформатором сопротивления, а задача подбора схемы с заданными свойствами (в рассматриваемом примере четырёхполюсника) называется задачей синтеза электрической цепи. В разделах курса «Линейные цепи постоянного тока», «Линейные цепи синусоидального тока» изучен вопрос об условиях передачи максимальной активной мощности от активного двухполюсника к пассивному. При полной компенсации реактивной мощности в цепи генератора, что имеет место в условиях рассматриваемой задачи 5.8,а, это условие выражается равенством rв = rн. Таким образом, первое расчётное уравнение для синтеза четырёхполюсника принимает вид: Z1 = 2. Рассматривая левую часть схемы рис. 5.12,б по отношению к выход-ным зажимам 2-2¢ четырёхполюсника как эквивалентный генератор с внут-ренним сопротивлением Z2 пассивной части схемы, запишем условие пере-дачи максимальной мощности от эквивалентного генератора в нагрузку rн: Z2 = Для определения четырёх коэффициентов А, В, С, D требуется система четырёх линейно независимых уравнений. Третье расчётное уравнение определяется свойством коэффициентов четырёхполюсника АD – ВС = 1. (3) Недостающее четвёртое уравнение позволяет нам свободу выбора вплоть до принятия одного коэффициента любым комплексным числом. Таким образом, задача синтеза четырёхполюсника, необходимого для увеличения передаваемой мощности в приёмник, имеет бесконечно большое число решений. Обычно для получения четвёртого расчётного уравнения поступают одним из двух способов: 1. Синтезируют симметричный четырёхполюсник, когда А = D и для реализации принимают простейшие из схем: Т-образный или П-образный четырёхполюсник; 2. Принимают коэффициент D = 1, и тогда и Т-, и П-схема превраща-ется в несимметричную Г-схему вида рис. 5.14,а. Приведём решение обоих вариантов. 1. Синтез симметричного четырёхполюсника. Коэффициенты искомого четырёхполюсника определяются системой уравнений:
Приведём подробное решение системы:
D×rв + В = С×rв×rн + А×rн. уравнение из первого. Получим: А×(rн – rв) = А×(rв – rн), откуда А = 0 = D. Для определения двух оставшихся коэффициентов решаем систему уравнений, в которой учтено А = D = 0: В = С×rв×rн; -ВС = 1, откуда В = ±j причём с учётом -ВС = 1 знаки при мнимой единице j должны быть одина-ковыми для В и С. Получаем два варианта решения: а) А = D = 0; б) А = D = 0; В = +j С = +j Рассчитываем параметры типовых Т- и П-схем четырёхполюсников по известным коэффициентам: - для Т-схемы Z1Т = Z2Т = - для П-схемы Z1П = Z2П = В ответах верхние знаки относятся к варианту а), нижние – к варианту б). Соответствующие схемы с указанием сопротивлений в Ом приведены на рис. 5.13.
ток в цепи генератора станет I1 = активная мощность на входе четырёхполюсника Р1max = I 2×Z1= 50 2×1 = 2500 Вт. Так как четырёхполюсник выполнен из реактивных элементов, не имеет потерь, то активная мощность приёмника Р2max = Р1max = 2500 Вт вместо Р2= 900 Вт исходной схемы рис. 5.12,а. 2. Синтез Г-схемы четырёхполюсника. Коэффициенты искомой схемы четырёхполюсника определим решением системы уравнений
Из этой системы получаем два варианта решения: а) А =
б) А =  ; В = -j2 ; В = -j2 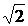 Ом; С = -j Ом; С = -j  См; D = 1; См; D = 1;
Этим вариантам соответствуют только две Г-схемы, приведенные на рис. 5.14. На рис. 5.14 сопротивления индуктивных и ёмкостных элементов представлены в Ом. Здесь так же, как и в случае применения схем рис. 5.13 Р1max = Р2max = 2500 Вт, I1= Ток нагрузки можно определить по формуле I2= Например, для схемы рис. 5.14,а он равен
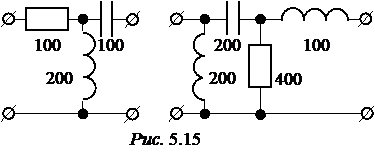
ЗАДАЧА 5.11. Эквива-лентность четырёхполюсни-ков. Сопротивления элемен-тов на схемах (рис. 5.15) даны в Омах. Необходимо показать, что приведенные четырёхполюсники эквивалентны. Указания. Поскольку четырёхполюсники обратимы, достаточно сравнить значения сопротивлений Z1Х, Z1К у обоих 4-полюсников. В нашем примере: Z1Х = 100 + j200 Ом, Z1К = 100 – j200 Ом, Z2Х = +j100 Ом, Z2К = 80 – j 60 Ом. Значения сопротивлений со вторичных зажимов приведены просто для контроля.
Определить А-коэффициенты четырёхполюсника и найти токи при разомкнутом рубильнике. Методические указания: необходимо записать уравнения для режима короткого замыкания. Это позволит найти А-коэффициенты 4-полюсника. Ответы: I1 = 3 мA, I2 = 1,2 мА.
Ответы: U1 = 54,65×е j38,52° В, I1 = 5,777×е j51,8° А, Zc = 9,46×е –j13,28° Ом. Задача 5.14. Четырёхполюсник с известными А-параметрами (А = = 0,5; В =10 + j10 Ом; С = -j0,05 См; D =1 – j1) собран по Т-схеме (рис. 5.17) и нагружен сопротивлением ZH = 20×е +j90° Ом. Требуется рассчитать токи на входе и выходе четырёхполюсника, построить векторную диаграмму. Методические указания: начать следует с определения сопротивлений четырёхполюсника. Они будут нужны для построения векторной диаграммы. Ответы: I1 = 20 – j10 А; I2 = 10 A.
Задача 5.15. Для симметричного четырёхполюсника экспериментально установлено, что Z1Х = 10×е +j90° Ом, Z2К = 10×е +j30° Ом. Требуется определить А-параметры четырёхполюсника и угол сдвига фаз между входными напряжением и током при согласованной нагрузке. Ответы: А = D = 1·е -j30°; В = 10 Ом; С = 0,1×е –j120° См; j = jC = 60°. |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 685. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 Способ 1. Рассматривается схема, нагруженная произвольным сопротивлением Z2, когда напряжение U2 и ток I2 отличны от нуля. Полученная схема описывается системой уравнений Кирхгофа. Методом подстановки избавляются от промежуточных токов и напряжений, приводя систему уравнений к виду: U1 = А·U2 + В·I2;
Способ 1. Рассматривается схема, нагруженная произвольным сопротивлением Z2, когда напряжение U2 и ток I2 отличны от нуля. Полученная схема описывается системой уравнений Кирхгофа. Методом подстановки избавляются от промежуточных токов и напряжений, приводя систему уравнений к виду: U1 = А·U2 + В·I2; = С·U2 + D·I2,
= С·U2 + D·I2, =
=  = -j0,05 См, D = 1;
= -j0,05 См, D = 1; ) + I2×(r – jxС ) = А·U2 + В·I2.
) + I2×(r – jxС ) = А·U2 + В·I2. = 0,5 – j0,5 = 0,5
= 0,5 – j0,5 = 0,5  ·е -j·45°,
·е -j·45°,
 = С·U2Х ; U1Х = I1Х ×(r – jxС) + U2Х = U2Х ×(1 +
= С·U2Х ; U1Х = I1Х ×(r – jxС) + U2Х = U2Х ×(1 +  =
=  = 20 Ом.
= 20 Ом. =
=  .
. е -j·45°; А2 =
е -j·45°; А2 =  =
=  = -j0,05 См;
= -j0,05 См; =
=  =
=  =
= 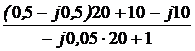 =
=  = 20 Ом.
= 20 Ом. Задача 5.2. Определить коэффициенты A, B, C, D несимметричного четырёхполюсника, собран-ного по Т-схеме (рис. 5.5), если
Задача 5.2. Определить коэффициенты A, B, C, D несимметричного четырёхполюсника, собран-ного по Т-схеме (рис. 5.5), если Задача 5.3. Найти элементы матри-цы [H] несимметричного четырёхполюсни-ка, собранного по П-схеме (рис. 5.6), если: r1 =10 Ом, r2 =20 Ом, x2 =20 Ом, х3 = 40 Ом. Используя основные уравнения четырёхпо-люсника в форме [H], определить напря-жение на входе при разомкнутых выходных зажимах, если U2X = 100 В.
Задача 5.3. Найти элементы матри-цы [H] несимметричного четырёхполюсни-ка, собранного по П-схеме (рис. 5.6), если: r1 =10 Ом, r2 =20 Ом, x2 =20 Ом, х3 = 40 Ом. Используя основные уравнения четырёхпо-люсника в форме [H], определить напря-жение на входе при разомкнутых выходных зажимах, если U2X = 100 В.  ЗАДАЧА 5.4. Для составления П-схемы заме-щения ЛЭП (рис. 5.7) и определения её входного сопротивления поставлены опыты холостого хода и короткого замыкания: U1X = 30 кВ, I1Х = 6 А, Р1Х = 27 кВт, φ1Х < 0; U1К = 4,5 кВ, I1К = 30 А, Р1К = 69 кВт, φ1К > 0.
ЗАДАЧА 5.4. Для составления П-схемы заме-щения ЛЭП (рис. 5.7) и определения её входного сопротивления поставлены опыты холостого хода и короткого замыкания: U1X = 30 кВ, I1Х = 6 А, Р1Х = 27 кВт, φ1Х < 0; U1К = 4,5 кВ, I1К = 30 А, Р1К = 69 кВт, φ1К > 0. ЗАДАЧА 5.5. Известны уравнения А-формы четырёхполюсника:
ЗАДАЧА 5.5. Известны уравнения А-формы четырёхполюсника:
 = 40 +
= 40 +  = 40 + 80 = 120 Ом,
= 40 + 80 = 120 Ом,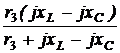 = 60 +
= 60 +  = 60 + j20 = 63,25×e j18,44° Ом,
= 60 + j20 = 63,25×e j18,44° Ом, =
=  =
= =
= 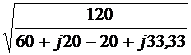 = ±1,342×e –j26,57° = ±(1,2 – j0,6).
= ±1,342×e –j26,57° = ±(1,2 – j0,6).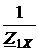 ×А =
×А =  = 0,0112×e –j26,57° = 0,01 – j0,005 См,
= 0,0112×e –j26,57° = 0,01 – j0,005 См, ×А =
×А =  ×1,342×e –j26,57° = 0,707×e –j8,13° = 0,7 – j0,1.
×1,342×e –j26,57° = 0,707×e –j8,13° = 0,7 – j0,1. =
=  = 2,05×e j29,0° А,
= 2,05×e j29,0° А,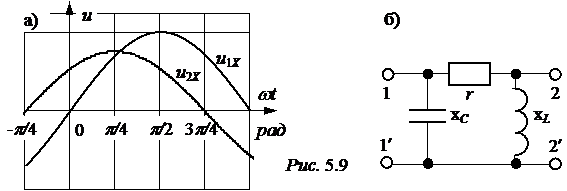
 = 1000
= 1000  = 500
= 500  = ±
= ±  =
=  e j(Yu1x – Yu2x) = ае ja.
e j(Yu1x – Yu2x) = ае ja. = +45°.
= +45°.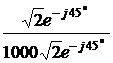 = 0,001 См,
= 0,001 См, =
=  =
= 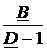 =
=  = -j1000 Ом – ёмкостное сопротивление;
= -j1000 Ом – ёмкостное сопротивление; =
=  = j1000 Ом – индуктивное сопротивление;
= j1000 Ом – индуктивное сопротивление; ×e j90° мA = 10 -2
×e j90° мA = 10 -2  = 877×e –j52,13° Ом.
= 877×e –j52,13° Ом. ) получаем
) получаем =
=  = 3,92×e j56,31° B.
= 3,92×e j56,31° B. =
=  = 7,84×10 -3e j56,31° A.
= 7,84×10 -3e j56,31° A. ) = Re(12,4×e j37,87°×10 -2
) = Re(12,4×e j37,87°×10 -2  =
=  = 0,286.
= 0,286.
 = 1 + (-j5)/(j70) = 0,928;
= 1 + (-j5)/(j70) = 0,928; = -j5 – j10 +
= -j5 – j10 + 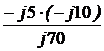 = -j15,70 Ом;
= -j15,70 Ом; =
=  = -j0,0143 См;
= -j0,0143 См; = 1 +
= 1 +  = 0,857.
= 0,857. =
=  = 3 А.
= 3 А. ×100 =
×100 =  ×100 = 2%, что допустимо при выполнении расчётов с указанной точностью.
×100 = 2%, что допустимо при выполнении расчётов с указанной точностью.

 =
=  = 10 А,
= 10 А, .
. = rн. (2)
= rн. (2) = rв;
= rв;  А×rн + В = С×rв×rн + D×rв, учтём А = D, а затем вычтем второе
А×rн + В = С×rв×rн + D×rв, учтём А = D, а затем вычтем второе , С = ±j
, С = ±j  ,
, = j3 Ом; В = -j
= j3 Ом; В = -j  См. С = -j
См. С = -j  = ± j3 Ом, Z0Т =
= ± j3 Ом, Z0Т = 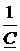 =
=  j3 Ом.
j3 Ом.
 =
=  = 50 А,
= 50 А,
 =
= 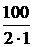 = 50 А.
= 50 А.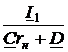 .
. I2=
I2=  =
=  ×e –j70,53° А.
×e –j70,53° А. Задача 5.12. Симметричный 4х-полюсник с rнг = 5 кОм питается от источника Е1 = 48 В (рис. 5.12б). При замкнутом рубильнике S ток на входе I1 = 3,2 мA, на выходе I2 = 1,6 мА.
Задача 5.12. Симметричный 4х-полюсник с rнг = 5 кОм питается от источника Е1 = 48 В (рис. 5.12б). При замкнутом рубильнике S ток на входе I1 = 3,2 мA, на выходе I2 = 1,6 мА. Задача 5.13. На выходе симметричного 4х-полюсника, нагруженного на сопротивление Zнг = Zc и имеющего коэффи-циенты A = 1+ j1, B = 10 + j10 Ом, протекает ток I2 = 2 A. Рассчитайте ток и напряжение на входе четырёхполюсника.
Задача 5.13. На выходе симметричного 4х-полюсника, нагруженного на сопротивление Zнг = Zc и имеющего коэффи-циенты A = 1+ j1, B = 10 + j10 Ом, протекает ток I2 = 2 A. Рассчитайте ток и напряжение на входе четырёхполюсника.