
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные понятия математической логикиАлгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности и ложности) и логических операций над ними [4]. Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно [4]. Для обозначения истины (истинного высказывания) используется символ 1, а для обозначения лжи (ложного высказывания) используется символ 0. Рассмотрим примеры логических высказываний (см. Таблицу 1): Таблица 1. Примеры логических выражений
Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если…то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить более сложные высказывания. Такие слова и словосочетания называют логическими связками. Высказывания, образованные с помощью логических связок – называют составными высказываниями. Высказывания, не являющиеся составными, называют элементарными.  Для обозначения логических высказываний, им назначают имена. Например, если А – высказывание «В четверг был дождь», В – высказывание «В пятницу было солнечно», то составное высказывание «В четверг был дождь, а в пятницу было солнечно», можно записать в виде: А и В. Здесь А, В – логические высказывания (могут быть либо истинными, либо ложными), и – логическая связка. Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (см. Таблицу 2): Таблица 2. Логические связки
Импликацию можно выразить через дизъюнкцию и отрицание: A → B = А Ú B (1) Эквивалентность можно выразить через отрицание, дизъюнкцию и конъюнкцию: A « B = (А Ú B) Ù (B Ú А) (2) Вычисление значения логического выражения производится слева направо в соответствии с таблицей истинности (см. Таблицу 3) и приоритетом выполнения логических операций (см. Таблицу 4). Порядок выполнения операций можно менять, используя круглые скобки. Таблица 3. Таблица истинности
Таблица 4. Приоритет выполнения логических операций
ТЕСТОВЫЕ ВОПРОСЫ К ТЕМЕ 3 1. Логическое отрицание называется ... A) импликация B) дизъюнкция С) эквивалентность D) конъюнкция E) инверсия 2. Логтческое умножения – это A) дизъюнкция B) импликация C) инверсия D) конъюнкция E) эквивалентность 3.Логическое сложение соответствует союзу ... A) тогда и только тогда, когда если …, то … B) если …, то … C) или D) не E) и 4. Логическое сложение называется ... A) Эквивалентность B) Инверсия C) Импликация D) Конъюнкция E) Дизъюнкция
5. Логическое умножение обозначается ... A) V B) <-> C) -> D) подчеркиванием сверху E) ^, & 6. Логическое сложение обозначается ... A) <-> B) ^, & C) -> D) V E) подчеркиванием сверху 7. Логика - это ... A) Наука о компьютерах B) Наука о доказательствах C) Наука о формах и способах мышления D) Наука о способах моделирования E) Наука о построении схем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 533. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
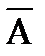 ,
Not
,
Not