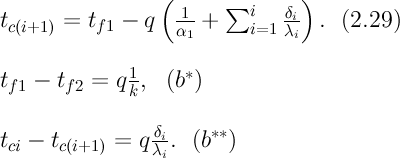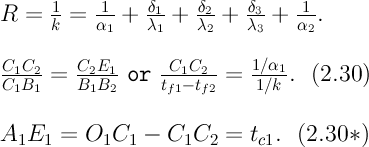Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Дифференциальные уравнения процесса теплообмена.
Отношение данных субстанций к объему обозначим буквой Е. Для объема: 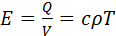 , для массы: , для массы: 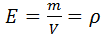 . Для переноса количества движения . Для переноса количества движения 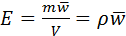 . Полное изменение Е в объеме V будет равно: . Полное изменение Е в объеме V будет равно: 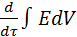 . Часть субстанции переносится из объема молекулярным путем. Поток субстанции через поверхность F, ограничивает данный объем, равен: . Часть субстанции переносится из объема молекулярным путем. Поток субстанции через поверхность F, ограничивает данный объем, равен: 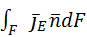 , где , где 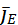 -плотность потока, переносимая субстанцией, -плотность потока, переносимая субстанцией, 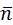 - еденичный вектор нормали данной поверхности.Используя формулу Остроградского-Гауса: - еденичный вектор нормали данной поверхности.Используя формулу Остроградского-Гауса: 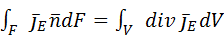 ; Беря во внимание закон сохранения субстанции можно сказать, что изменение субстанции по времени будет равно: ; Беря во внимание закон сохранения субстанции можно сказать, что изменение субстанции по времени будет равно: 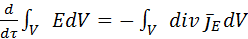 . Считая подынтегральные функции непрерывными можно записать: . Считая подынтегральные функции непрерывными можно записать: 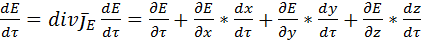 , где , где 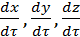 - Проекции скоростей, - Проекции скоростей, 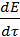 - локальное изменение плотности субстанции. - локальное изменение плотности субстанции. 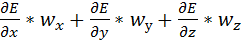 . Для процесса теплопроводности . Для процесса теплопроводности 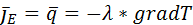 , поэтому можно записать, что , поэтому можно записать, что 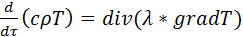 - дифференциальное уравнение теплопроводности. Фурье-Кирхгофа для неподвижного тела: - дифференциальное уравнение теплопроводности. Фурье-Кирхгофа для неподвижного тела: 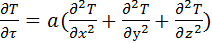 (1), a= (1), a= 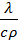 -температуропроводность -температуропроводность 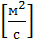 , чем больше а, тем меньше тепловая инерционность.Скорость изменения температуры в любой точке тел, имеющих большую тепловую инерционность, скорость будет меньше, чем тел с малой тепловой интенсивностью. Температуропроводность зависит от состава, физического строения, состояния и свойств тела. , чем больше а, тем меньше тепловая инерционность.Скорость изменения температуры в любой точке тел, имеющих большую тепловую инерционность, скорость будет меньше, чем тел с малой тепловой интенсивностью. Температуропроводность зависит от состава, физического строения, состояния и свойств тела. 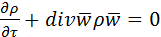 (2)- уравнение сплошности или неразрывности. Для переноса количества движения и предположения, что жидкость несжимаема и (2)- уравнение сплошности или неразрывности. Для переноса количества движения и предположения, что жидкость несжимаема и 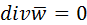 , можно получить следующее уравнение: , можно получить следующее уравнение: 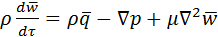 (3). (3). 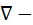 оператор Гомельтона. Для описания теплообмена в общем виде необходимо воспроизвести систему диф. уравнений , состоящих из трех приведенных (1),(2),(3). оператор Гомельтона. Для описания теплообмена в общем виде необходимо воспроизвести систему диф. уравнений , состоящих из трех приведенных (1),(2),(3).
42.. Краевые условия теплоотдачи.
Чтобы уравнение температурного поля отвечала конкретному рассматриваемому случаю, необходимо к дифференциальному уравнению ( 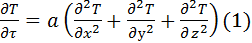 ) добавить условие однородности или единственности решения. К данным условием относятся геометрические и физические характеристики тела, временные или начальные условия и граничные условия. Начальные и граничные условия в совокупности называют краевыми условиями. В качестве начальных условий принято задавать распределение температур внутри тела в начальный момент времени. ) добавить условие однородности или единственности решения. К данным условием относятся геометрические и физические характеристики тела, временные или начальные условия и граничные условия. Начальные и граничные условия в совокупности называют краевыми условиями. В качестве начальных условий принято задавать распределение температур внутри тела в начальный момент времени. 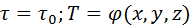 В самом простом случае: В самом простом случае: 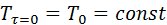 . Граничные условия определяют особенности взаимодействия изучаемого тела с окружающей средой. Различают граничные условия 1-го, 2-го, 3-го и 4-го рода. Граничные условия 1-го рода задаются распределением температур тела на поверхности в любой момент времени. В частности для стац. задачи принимается . Граничные условия определяют особенности взаимодействия изучаемого тела с окружающей средой. Различают граничные условия 1-го, 2-го, 3-го и 4-го рода. Граничные условия 1-го рода задаются распределением температур тела на поверхности в любой момент времени. В частности для стац. задачи принимается 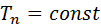 . Граничные условия 2-го рода задаются распределением плотности теплового потока на поверхности тела в любой момент времени . Граничные условия 2-го рода задаются распределением плотности теплового потока на поверхности тела в любой момент времени 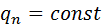 . Граничные условия 3-го рода характеризуют закон конвективного теплообмена между поверхностью тела и окружающей средой в соответствии с уравнением Ньютона-Рихмана. Граничные условия 4-го рода- условие сопряжения соотв. теплообмена соприкасающихся тел, когда температура тел в зоне контакта одинакова. Дифференциальное уравнение(1) Фурье-Кирхгофа вместе с краевыми условиями полностью определяют задачу теплопроводности и позволяет найти такую единичную функцию, которая является решением конкретной исследуемой задачи . Граничные условия 3-го рода характеризуют закон конвективного теплообмена между поверхностью тела и окружающей средой в соответствии с уравнением Ньютона-Рихмана. Граничные условия 4-го рода- условие сопряжения соотв. теплообмена соприкасающихся тел, когда температура тел в зоне контакта одинакова. Дифференциальное уравнение(1) Фурье-Кирхгофа вместе с краевыми условиями полностью определяют задачу теплопроводности и позволяет найти такую единичную функцию, которая является решением конкретной исследуемой задачи 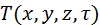 . .
43.Теплопроводность при граничных условиях 1 рода. Плоская стенка.
 Допускаем, что материалы однородны и изотропны. Коэффициент теплопроводности Допускаем, что материалы однородны и изотропны. Коэффициент теплопроводности 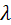 принимаем постоянным и исследуемый режим-стационароным: принимаем постоянным и исследуемый режим-стационароным: 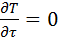 . В качестве граничного условия 1-го рода задается . В качестве граничного условия 1-го рода задается 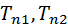 . Целью решения задач является определение изменения температур вдоль координаты x. . Целью решения задач является определение изменения температур вдоль координаты x. 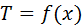 . Плоская стенка: Полагаем, что длина и ширина стенки на много больше ее толщины. Ось OX направлена по нормали к поверхности стенки. . Плоская стенка: Полагаем, что длина и ширина стенки на много больше ее толщины. Ось OX направлена по нормали к поверхности стенки. 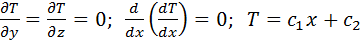 , где , где 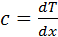 изменяется по линейному закону. изменяется по линейному закону. 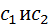 определяются из граничных условий определяются из граничных условий 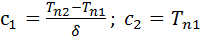 . Зная . Зная 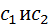 можно утверждать, что можно утверждать, что 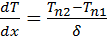 .Уравнение Фурье: .Уравнение Фурье: 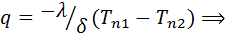 Плоскость теплового насоса прямопропорциональна перепаду температур на стенке и обратнопропорциональна толщине стенки. Общее количество теплоты, передаваемое через поверхность за время Плоскость теплового насоса прямопропорциональна перепаду температур на стенке и обратнопропорциональна толщине стенки. Общее количество теплоты, передаваемое через поверхность за время  : : 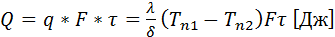 . .
44.Теплопроводность при граничных условиях 1 рода. Многослойная плоская стенка.
Допускаем, что материалы однородны и изотропны. Коэффициент теплопроводности 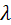 принимаем постоянным и исследуемый режим- стационароным: принимаем постоянным и исследуемый режим- стационароным: 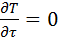 . В качестве граничного условия 1-го рода задается . В качестве граничного условия 1-го рода задается 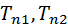 . Целью решения задач является определение изменения температур вдоль координаты x. . Целью решения задач является определение изменения температур вдоль координаты x. 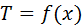 . Многослойная плоская стенка: При стационарном решении плотности теплового потока, проходящие через каждую стенку, если величина постоянная. . Многослойная плоская стенка: При стационарном решении плотности теплового потока, проходящие через каждую стенку, если величина постоянная. 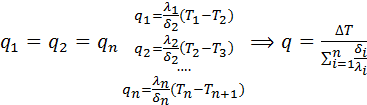
45.Теплопроводность при граничных условиях 1 рода. Цилиндрическая стенка.
Допускаем, что материалы однородны и изотропны. Коэффициент теплопроводности 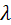 принимаем постоянным и исследуемый режим- стационароным: принимаем постоянным и исследуемый режим- стационароным: 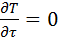 . В качестве граничного условия 1-го рода задается . В качестве граничного условия 1-го рода задается 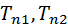 . Целью решения задач является определение изменения температур вдоль координаты x. . Целью решения задач является определение изменения температур вдоль координаты x. 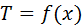 . Цилиндрическая стенка: Температура стенки будет изменятся только вдоль радиуса. . Цилиндрическая стенка: Температура стенки будет изменятся только вдоль радиуса. 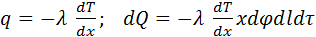 Учитывая, что Учитывая, что 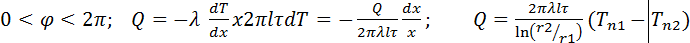 . Для цилиндрической трубы используется понятие теплового потока, отнесенного к площади внутренней поверхности, к наружной поверхности и к длине трубы. . Для цилиндрической трубы используется понятие теплового потока, отнесенного к площади внутренней поверхности, к наружной поверхности и к длине трубы. 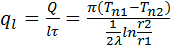 минимальное термическое сопротивление цилиндрической стенки. минимальное термическое сопротивление цилиндрической стенки.
46.Теплопроводность при граничных условиях I рода. Шаровая стенка.
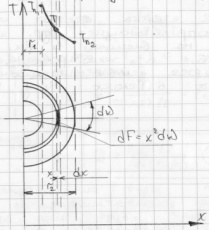
Шаровую стенку пронизывают тепловым потоком: 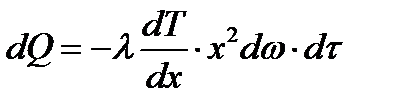 . Учитывая, что . Учитывая, что 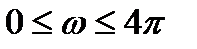 , то после интегрирования: , то после интегрирования:
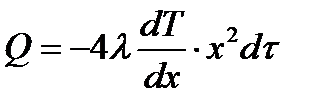 ; ; 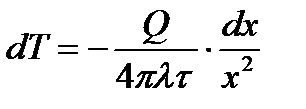 . .
Учитывая, что 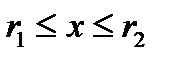 , а , а 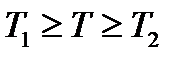 , мы можем получить: , мы можем получить: 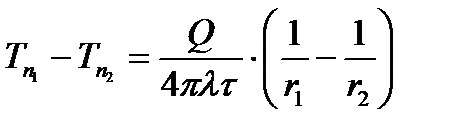
Откуда: 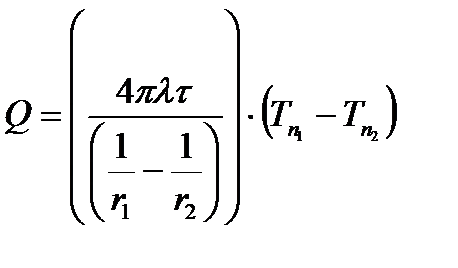 . .
Откуда следует, что при стационарном режиме в шаровой стенке температура изменяется по гиперболе.
47.Теплопроводность при граничных условиях III рода. Плоская стенка.
Плоская стенка, толщиной δ и теплопроводностью материала λ, разделяет две среды с темп T1 и T2. Коэффициенты теплоотдачи со стороны среды 1 – α1. Считается, что T1, T2, α1, α2, λ – есть величины постоянные. Из этого следует: T=f(x).
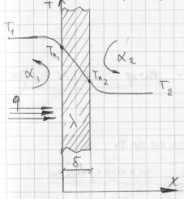
Процесс стационарный:
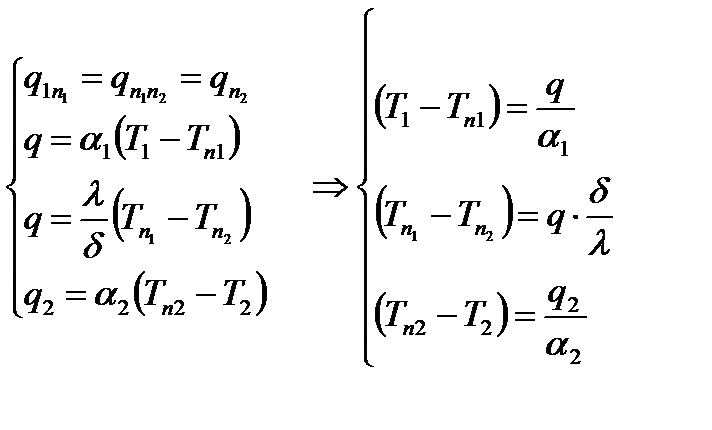
Складываем: 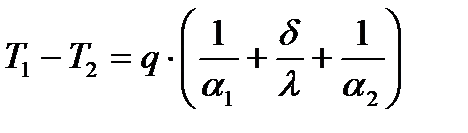
Выразим q: 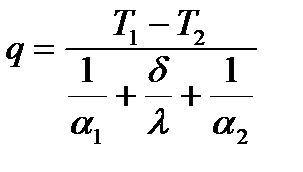 ; ; 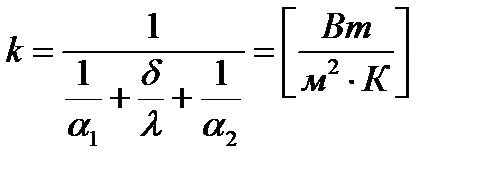
- коэф теплопередачи
Используя k , можно записать: 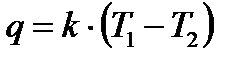 - ур-е теплопередачи. - ур-е теплопередачи.
Величина 1/kназ полным термическим сопротивлением передачи.
48. Теплопроводность при граничных условиях III рода. Многослойная плоская стенка
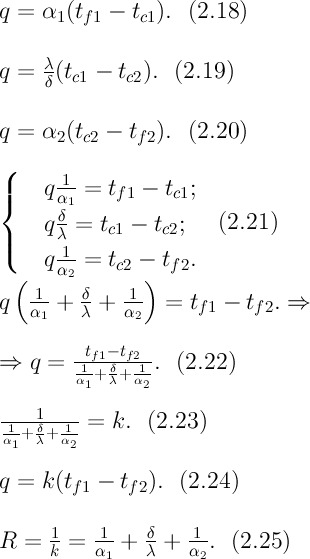 Граничные условия третьего рода (теплопередача). Передача теплоты из одной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде. Граничные условия третьего рода (теплопередача). Передача теплоты из одной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде.
Рассмотрим теплопередачу через однородную и многослойную плоские стенки.
Пусть плоская однородная стенка имеет толщину δ (рис. 2.3). Заданы коэффициент теплопроводности стенки λ, температуры окружающей среды tf1 иtf2, а также коэффициенты теплоотдачи 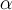 1 и 1 и 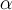 2; будем считать, что величины tf1, tf2 , 2; будем считать, что величины tf1, tf2 , 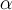 1 и 1 и 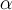 2 постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки. 2 постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки.
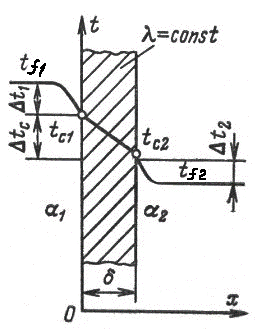
Рис. 2.3. Теплопередача через плоскую стенку.
При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки. Плотность теплового потока от горячей жидкости к стенке определяется уравнением (2.18)
При стационарном тепловом режиме та же плотность теплового потока, обусловленная теплопроводностью через твердую стенку - (2.19). Тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи - (2.20). Уравнения (2.18) - (2.20) можно собрать в систему (2.21). Если сложить равенства (2.21) почленно, то получим выражение из которого находим плотность теплового потока, Вт/м2 - (2.22). Если ввести обозначение (2.23) (единица измерения - Вт/м2×К), то уравнение (2.22) можно записать в виде (2.24). Величина k имеет ту же размерность, что и 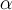 , и называется коэффициентом теплопередачи. Коэффициент теплопередачи kхарактеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус. , и называется коэффициентом теплопередачи. Коэффициент теплопередачи kхарактеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.
Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи - (2.25). Из (2.25) видно, что полное термическое сопротивление складывается из частных термических сопротивлений 1/ 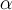 1, δ/λ и 1/ 1, δ/λ и 1/ 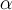 2, причем 1/ 2, причем 1/ 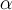 1=R1 — термическое сопротивление теплоотдачи от горячей жидкости к поверхности стенки; δ/λ=Rс — термическое сопротивление теплопроводности стенки;1/ 1=R1 — термическое сопротивление теплоотдачи от горячей жидкости к поверхности стенки; δ/λ=Rс — термическое сопротивление теплопроводности стенки;1/ 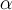 2=R2 — термическое сопротивление теплоотдачи от поверхности стенки к холодной жидкости. 2=R2 — термическое сопротивление теплоотдачи от поверхности стенки к холодной жидкости.
Поскольку общее термическое сопротивление состоит из частных термических сопротивлений, то совершенно очевидно, что для многослойной стенки нужно учитывать термическое сопротивление каждого слоя. Если стенка состоит из nслоев, то полное термическое сопротивление теплопередачи через такую стенку будет равно:
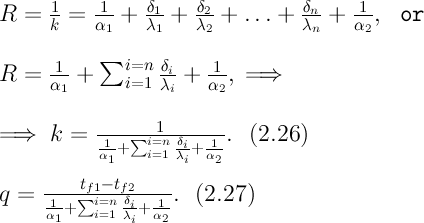
Плотность теплового потока через многослойную стенку, состоящую из n слоев, будет равна - (2.27). Уравнение (2.27) для многослойной стенки подобно уравнению (2.24) для однородной плоской стенки. Различие заключается в выражениях для коэффициентов теплопередачи k. При сравнении уравнений (2.26) и (2.23) видно, что соотношение (2.23) является частным случаем уравнения (2.26), когда n=1.
Тепловой поток Q, Вт, через поверхность F твердой стенки равен: 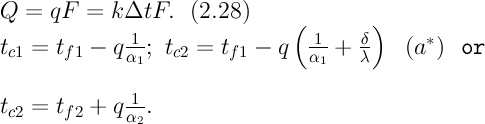
Температуры поверхностей однородной стенки можно найти из уравнений (2.21). Из них следует - (а*). Из сопоставления уравнений (2.15) и (2.27) следует, что передача теплоты через многослойную стенку при граничных условиях первого рода является частным случаем общего случая передачи теплоты при граничных условиях третьего рода.
На основании сказанного температура на границе любых двух слоев 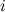 и и 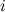 +1 при граничных условиях третьего рода может быть определена по уравнению: +1 при граничных условиях третьего рода может быть определена по уравнению: 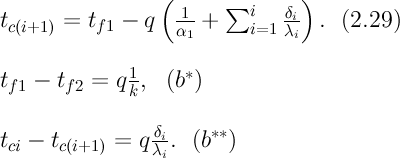
Наряду с уравнением (2.29) для расчета гранитных температур применяются и графические методы.
Рассмотрим графический метод определения температур на поверхности слоев неоднородной стенки, в основу которого положено свойство линейной зависимости температурного напора в стенке от ее термического сопротивления - (b*) или для любого слоя - (b**). Такая зависимость дает возможность построить фиктивную стенку, в которой толщины слоев будут пропорциональны соответствующим термическим сопротивлениям, а внешние термические сопротивления теплоотдачи 1/ 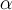 1 и 1/ 1 и 1/ 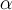 2 учитываются путем введения двух условных граничных слоев соответствующей толщины. Сущность метода поясним на примере трехслойной стенки. 2 учитываются путем введения двух условных граничных слоев соответствующей толщины. Сущность метода поясним на примере трехслойной стенки.
Общее термическое сопротивление теплопередачи через такую стоику равно:
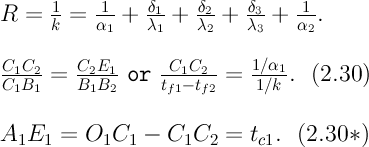
Отложим на горизонтали отрезки О1А1, А1А2, А2А3, А3А4, и А4О2, соответственно равные термическим сопротивлениям 1/ 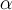 1, δ1/λ1, δ2/λ2, δ3/λ3 и 1/ 1, δ1/λ1, δ2/λ2, δ3/λ3 и 1/ 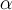 2 (рис. 2.4). В точках О1, А1, А2, А3, А4, О2 поставим перпендикуляры и на О1К1 и О2К2 отложим в некотором масштабе температуры подвижных сред tf1 и tf2. Соединим прямой линией точки С1 и В2. Отрезки А1Е1, А2Е2, А3Е3 и А4Е4 будут равны искомым температурам tc1, tc2, tc3 и tc4. Из подобия треугольников С1В1В2 и C1C2E1следует выражение (2.30). Из отношения (2.30) следует, что C1C2=tf1–tc1, следовательно, можно записать (2.30*). Аналогичным образом доказывается, что и отрезки А2Е2, А3Е3 и А4Е4 соответственно равны температурам tc2, tc3 и tc4. 2 (рис. 2.4). В точках О1, А1, А2, А3, А4, О2 поставим перпендикуляры и на О1К1 и О2К2 отложим в некотором масштабе температуры подвижных сред tf1 и tf2. Соединим прямой линией точки С1 и В2. Отрезки А1Е1, А2Е2, А3Е3 и А4Е4 будут равны искомым температурам tc1, tc2, tc3 и tc4. Из подобия треугольников С1В1В2 и C1C2E1следует выражение (2.30). Из отношения (2.30) следует, что C1C2=tf1–tc1, следовательно, можно записать (2.30*). Аналогичным образом доказывается, что и отрезки А2Е2, А3Е3 и А4Е4 соответственно равны температурам tc2, tc3 и tc4.
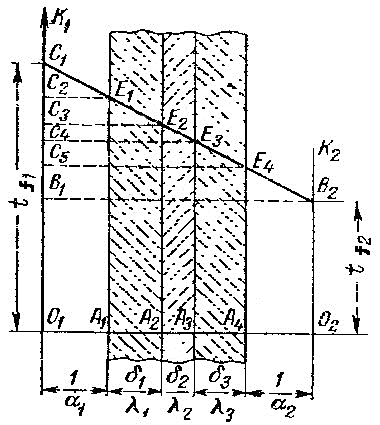
Рис. 2.4. Графический способ определения температур.
|


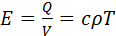 , для массы:
, для массы: 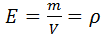 . Для переноса количества движения
. Для переноса количества движения 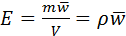 . Полное изменение Е в объеме V будет равно:
. Полное изменение Е в объеме V будет равно: 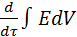 . Часть субстанции переносится из объема молекулярным путем. Поток субстанции через поверхность F, ограничивает данный объем, равен:
. Часть субстанции переносится из объема молекулярным путем. Поток субстанции через поверхность F, ограничивает данный объем, равен: 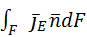 , где
, где 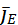 -плотность потока, переносимая субстанцией,
-плотность потока, переносимая субстанцией, 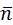 - еденичный вектор нормали данной поверхности.Используя формулу Остроградского-Гауса:
- еденичный вектор нормали данной поверхности.Используя формулу Остроградского-Гауса: 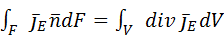 ; Беря во внимание закон сохранения субстанции можно сказать, что изменение субстанции по времени будет равно:
; Беря во внимание закон сохранения субстанции можно сказать, что изменение субстанции по времени будет равно: 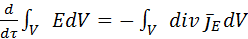 . Считая подынтегральные функции непрерывными можно записать:
. Считая подынтегральные функции непрерывными можно записать: 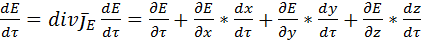 , где
, где 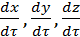 - Проекции скоростей,
- Проекции скоростей, 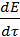 - локальное изменение плотности субстанции.
- локальное изменение плотности субстанции. 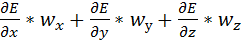 . Для процесса теплопроводности
. Для процесса теплопроводности 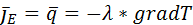 , поэтому можно записать, что
, поэтому можно записать, что 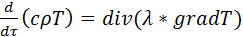 - дифференциальное уравнение теплопроводности. Фурье-Кирхгофа для неподвижного тела:
- дифференциальное уравнение теплопроводности. Фурье-Кирхгофа для неподвижного тела: 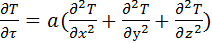 (1), a=
(1), a= 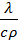 -температуропроводность
-температуропроводность 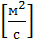 , чем больше а, тем меньше тепловая инерционность.Скорость изменения температуры в любой точке тел, имеющих большую тепловую инерционность, скорость будет меньше, чем тел с малой тепловой интенсивностью. Температуропроводность зависит от состава, физического строения, состояния и свойств тела.
, чем больше а, тем меньше тепловая инерционность.Скорость изменения температуры в любой точке тел, имеющих большую тепловую инерционность, скорость будет меньше, чем тел с малой тепловой интенсивностью. Температуропроводность зависит от состава, физического строения, состояния и свойств тела. 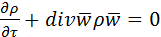 (2)- уравнение сплошности или неразрывности. Для переноса количества движения и предположения, что жидкость несжимаема и
(2)- уравнение сплошности или неразрывности. Для переноса количества движения и предположения, что жидкость несжимаема и 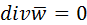 , можно получить следующее уравнение:
, можно получить следующее уравнение: 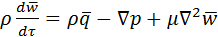 (3).
(3). 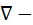 оператор Гомельтона. Для описания теплообмена в общем виде необходимо воспроизвести систему диф. уравнений , состоящих из трех приведенных (1),(2),(3).
оператор Гомельтона. Для описания теплообмена в общем виде необходимо воспроизвести систему диф. уравнений , состоящих из трех приведенных (1),(2),(3).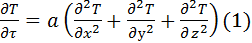 ) добавить условие однородности или единственности решения. К данным условием относятся геометрические и физические характеристики тела, временные или начальные условия и граничные условия. Начальные и граничные условия в совокупности называют краевыми условиями. В качестве начальных условий принято задавать распределение температур внутри тела в начальный момент времени.
) добавить условие однородности или единственности решения. К данным условием относятся геометрические и физические характеристики тела, временные или начальные условия и граничные условия. Начальные и граничные условия в совокупности называют краевыми условиями. В качестве начальных условий принято задавать распределение температур внутри тела в начальный момент времени. 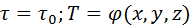 В самом простом случае:
В самом простом случае: 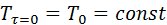 . Граничные условия определяют особенности взаимодействия изучаемого тела с окружающей средой. Различают граничные условия 1-го, 2-го, 3-го и 4-го рода. Граничные условия 1-го рода задаются распределением температур тела на поверхности в любой момент времени. В частности для стац. задачи принимается
. Граничные условия определяют особенности взаимодействия изучаемого тела с окружающей средой. Различают граничные условия 1-го, 2-го, 3-го и 4-го рода. Граничные условия 1-го рода задаются распределением температур тела на поверхности в любой момент времени. В частности для стац. задачи принимается 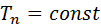 . Граничные условия 2-го рода задаются распределением плотности теплового потока на поверхности тела в любой момент времени
. Граничные условия 2-го рода задаются распределением плотности теплового потока на поверхности тела в любой момент времени 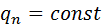 . Граничные условия 3-го рода характеризуют закон конвективного теплообмена между поверхностью тела и окружающей средой в соответствии с уравнением Ньютона-Рихмана. Граничные условия 4-го рода- условие сопряжения соотв. теплообмена соприкасающихся тел, когда температура тел в зоне контакта одинакова. Дифференциальное уравнение(1) Фурье-Кирхгофа вместе с краевыми условиями полностью определяют задачу теплопроводности и позволяет найти такую единичную функцию, которая является решением конкретной исследуемой задачи
. Граничные условия 3-го рода характеризуют закон конвективного теплообмена между поверхностью тела и окружающей средой в соответствии с уравнением Ньютона-Рихмана. Граничные условия 4-го рода- условие сопряжения соотв. теплообмена соприкасающихся тел, когда температура тел в зоне контакта одинакова. Дифференциальное уравнение(1) Фурье-Кирхгофа вместе с краевыми условиями полностью определяют задачу теплопроводности и позволяет найти такую единичную функцию, которая является решением конкретной исследуемой задачи 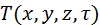 .
. Допускаем, что материалы однородны и изотропны. Коэффициент теплопроводности
Допускаем, что материалы однородны и изотропны. Коэффициент теплопроводности 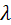 принимаем постоянным и исследуемый режим-стационароным:
принимаем постоянным и исследуемый режим-стационароным: 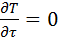 . В качестве граничного условия 1-го рода задается
. В качестве граничного условия 1-го рода задается 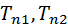 . Целью решения задач является определение изменения температур вдоль координаты x.
. Целью решения задач является определение изменения температур вдоль координаты x. 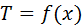 . Плоская стенка: Полагаем, что длина и ширина стенки на много больше ее толщины. Ось OX направлена по нормали к поверхности стенки.
. Плоская стенка: Полагаем, что длина и ширина стенки на много больше ее толщины. Ось OX направлена по нормали к поверхности стенки. 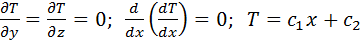 , где
, где 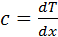 изменяется по линейному закону.
изменяется по линейному закону. 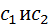 определяются из граничных условий
определяются из граничных условий 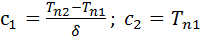 . Зная
. Зная 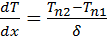 .Уравнение Фурье:
.Уравнение Фурье: 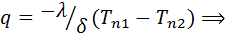 Плоскость теплового насоса прямопропорциональна перепаду температур на стенке и обратнопропорциональна толщине стенки. Общее количество теплоты, передаваемое через поверхность за время
Плоскость теплового насоса прямопропорциональна перепаду температур на стенке и обратнопропорциональна толщине стенки. Общее количество теплоты, передаваемое через поверхность за время  :
: 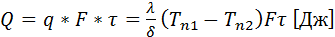 .
.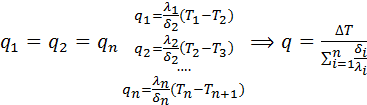
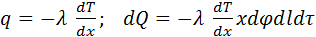 Учитывая, что
Учитывая, что 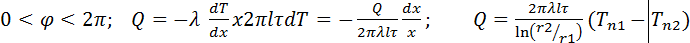 . Для цилиндрической трубы используется понятие теплового потока, отнесенного к площади внутренней поверхности, к наружной поверхности и к длине трубы.
. Для цилиндрической трубы используется понятие теплового потока, отнесенного к площади внутренней поверхности, к наружной поверхности и к длине трубы. 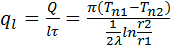 минимальное термическое сопротивление цилиндрической стенки.
минимальное термическое сопротивление цилиндрической стенки.
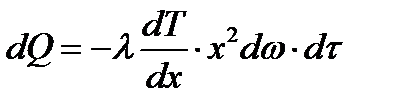 . Учитывая, что
. Учитывая, что 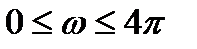 , то после интегрирования:
, то после интегрирования: 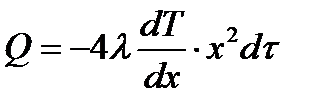 ;
; 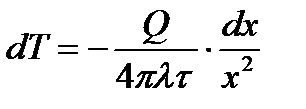 .
.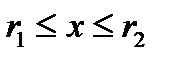 , а
, а 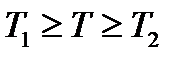 , мы можем получить:
, мы можем получить: 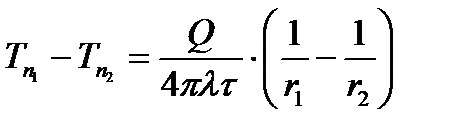
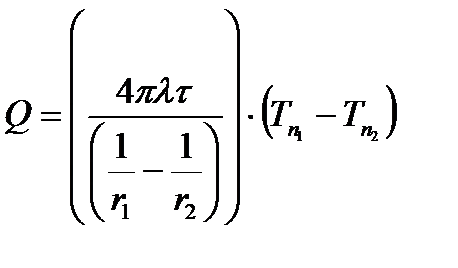 .
.
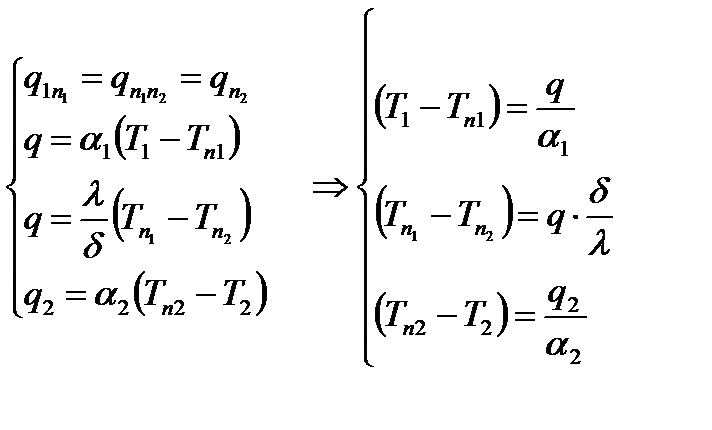
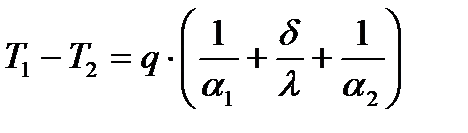
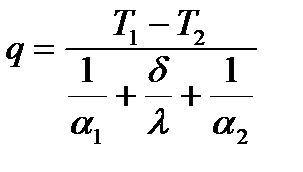 ;
; 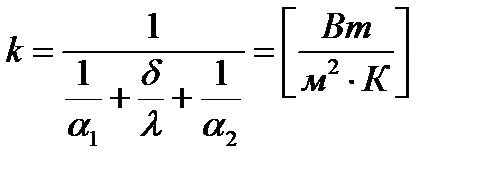
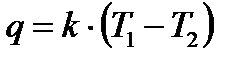 - ур-е теплопередачи.
- ур-е теплопередачи.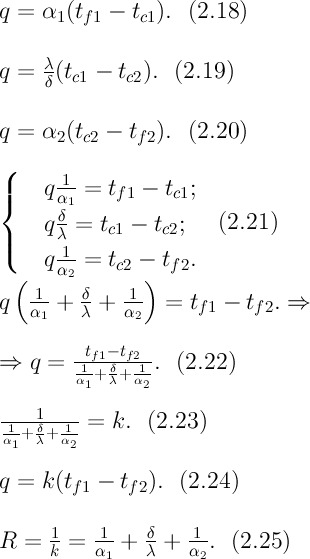 Граничные условия третьего рода (теплопередача). Передача теплоты из одной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде.
Граничные условия третьего рода (теплопередача). Передача теплоты из одной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде.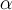 1 и
1 и 
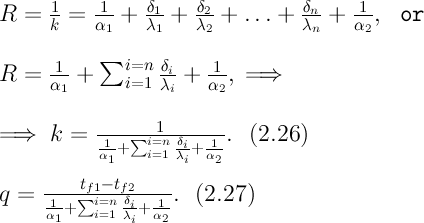
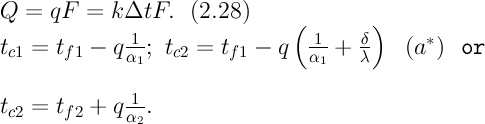
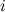 и
и