
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Инерциальные навигационные системы. Теоретические основыСтр 1 из 4Следующая ⇒ ГЛАВА 3. ГРАВИТАЦИОННАЯ И ИНЕРЦИАЛЬНАЯ ГРАВИМЕТРИЯ Для определения местоположения различных транспортных средств на суше, на море и в воздухе широко используются инерциальные навигационные системы. Инерциальный измерительный модуль содержит систему из трех взаимно перпендикулярных акселерометров и систему ориентации, содержащую набор гироскопов гирометров (инерциальная платформа). Измеряемой величиной согласно закону Ньютона является ускорение где Ускорение В системе координат, жестко связанной с вращающейся Землей, будут возникать ещё и центробежное и кориолисово ускорения, которые необходимо учитывать в В выражениях (3.1) и (3.2) была рассмотрена структура инерциального ускорения 10 мкм/с–2 , используют локальные аппроксимации гравитационного поля Земли. В спутниковых навигационных системах используют стандартную модель гравитационного поля Земли с гармониками до 10–го порядка включительно. Трехмерный вектор удельной силы  Из–за эквивалентности инерциального Таким образом, получая из измерений ускорения носителя, и учитывая гравитационное поле, мы имеем возможность, произведя двойное интегрирование, определять местоположение инерциальным методом. В этом случае участвуют три системы отсчета: 1. инерциальное ускорение определяется инерциальной системой отсчета (равноденственная система инерциальных координат (xoyz)i). 2. компоненты вектора удельной силы мы измеряем в системе связанной с осями акселерометра – эта инструментальная система координат, её ориентировка при движении носителя меняется 3. фиксированная относительно Земли, локальная система координат, связанная с гравитационным полем Земли. Её ориентировка меняется вследствие вращения Земли и из–за перемещения носителя по маршруту. При движении в этой системе поддерживается направление отвеса с помощью модели гравитационного поля Земли (чаще достаточно учитывать нормальную модель гравитационного поля). Такой вид ориентира получил название локально – уровенный. Таким образом, мы координаты пробной единичной массы в инерциальной системе координат определяем радиус вектором
С другой стороны в локально–уровенной системе координат та же единичная масса определяется радиус – вектором Переход от вектора Найдем связь между радиальной скоростью В выражениях (3.6) и (3.7) преобразуем матрицы, в которых взяты производные по времени. С этой целью подробнее рассмотрим матрицу Rij. При переходе от локальной системы в инерциальную необходимо редуцировать наблюдения с момента t на эпоху каталога T2000. С этой целью необходимо выполнить повороты на углы прецессии и нутации, т.е. воздействовать матрицами N×П, где N – матрица нутации, а П – матрица прецессии. Далее необходимо перейти к гринвичской системе, выполнив поворот матрицей S на угол равный звездному времени s. Далее матрицей Р привести мгновенные гринвичские координаты к среднему полюсу и ,наконец, перейти к локальной – уровеннойсистеме, выполнив поворот матрицей L, то есть: Rij = L×P×S×N×П (3.8) Из перечисленных матриц только S имеет сильную зависимость от времени (её аргументом является звёздное время s). Остальные матрицы от времени зависят слабо, т.е. меняются медленно: матрица прецессии П за год дает около 50" , матрица нутации N примерно 10" за период около 19 лет, матрица Р даёт за год менее 1". Матрица L напрямую зависит от длины маршрута, скорости и времени нахождения на маршруте. Для наземных измерений при передвижении транспортного средства матрица L будет меняться медленно. Поэтому полная производная от Rij, как от сложной функции, будет Обозначив где WÅ является матрицей проекций угловой скорости Земли. Возьмем вторую производную от (3.9) и далее с учетом (3.9) имеем: Выражение (3.5)–(3.7) с учетом (3.5), (3.9) и (3.11) приобретает вид: Аналогично тому, как был выполнен переход от инерциальной системы координат к гринвичской (ГЛАВА.1, параграф 1.1), можно в едином алгоритме выполнить переход от инерциальной системе к локальной. Введя обобщенный вектор состояний в локальной системе координат где Матрица (3.14) является блочной, каждый элемент которой состоит из 3–х мерных матриц. Первый столбец–блок этих 3–х мерных матриц умножается на вектор–столбец |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 232. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 – сила, m – масса,
– сила, m – масса,  – удельная сила, отнесенная к единице массы.
– удельная сила, отнесенная к единице массы. содержит в себе ускорение подвижного носителя
содержит в себе ускорение подвижного носителя  и гравитационное ускорение
и гравитационное ускорение  , то есть:
, то есть: (3.2)
(3.2) (3.3)
(3.3) (3.4)
(3.4) (удельный – значит отнесенный к единичной массе), измеренный в инерциальном пространстве, представляет собой разность вектора, характеризующего ускорение, полученное единичной массой в инерциальной системе координат, и гравитационного вектора
(удельный – значит отнесенный к единичной массе), измеренный в инерциальном пространстве, представляет собой разность вектора, характеризующего ускорение, полученное единичной массой в инерциальной системе координат, и гравитационного вектора 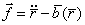 ( 3.4)
( 3.4)

 .
. осуществляется при помощи матрицы вращения Rij, элементы которой являются функциями углов поворота систем и времени t:
осуществляется при помощи матрицы вращения Rij, элементы которой являются функциями углов поворота систем и времени t: . (3.5)
. (3.5) в инерциальной и
в инерциальной и 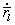 в локальной системе координат. Ту же самую связь найдем и для ускорений. С этой целью дважды выполним дифференцирование выражения (3.5). Имеем следующие формулы:
в локальной системе координат. Ту же самую связь найдем и для ускорений. С этой целью дважды выполним дифференцирование выражения (3.5). Имеем следующие формулы: (3.6)
(3.6) (3.7)
(3.7) или
или  , но
, но 
 , получим
, получим , (3.9)
, (3.9) – (3.10)
– (3.10) . (3.11)
. (3.11)

 и на основании выводов и обозначений ГЛАВЫ 1 (формулы 1.11–1.20) мы можем записать
и на основании выводов и обозначений ГЛАВЫ 1 (формулы 1.11–1.20) мы можем записать , (3.13)
, (3.13) –обобщенный вектор состояний в инерциальной системе координат, а матрица X¢il имеет аналогичную структуру матрицы (1.20) главы1, но с другими обозначениями, т.е.
–обобщенный вектор состояний в инерциальной системе координат, а матрица X¢il имеет аналогичную структуру матрицы (1.20) главы1, но с другими обозначениями, т.е.
 , второй – на
, второй – на  , а третий – на
, а третий – на  .
.