
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Случай разных совокупностей параметров g при разных значениях l⇐ ПредыдущаяСтр 20 из 20
Некоторые различия между рассматриваемыми правилами решения могут возникнуть, если разным значениям
где
Для того чтобы правило решения, получающееся минимизацией (6.5.18), было вполне определенным, необходимо как-то задать величины
где
ВЫВОДЫ
В следующих двух главах рассмотрим ряд важных деталей, связанных с применением адаптивного байесова подхода при параметрической и непараметрической априорной неопределенности, а сейчас, допуская некоторые повторения, кратко обсудим основные результаты этой главы. 1. Как и обычный байесов, адаптивный байесов подход основан на выборе правила решения u = u(x), минимизирующего ожидаемые при данном состоянии имеющихся знаний потери. Отличие заключается в том, что из-за недостатка априорных сведений вместо точной количественной меры ожидаемых потерь - апостериорного риска - вводится его оценка, максимально использующая имеющиеся данные наблюдения и ограниченные априорные сведения. Этот принцип применяется как при параметрической, так и при непараметрической априорной неопределенности.  2. Если использованная при нахождении адаптивного байесова правила решения оценка апостериорного риска состоятельна, то это правило удовлетворяет большинству из принципов предпочтения (принципов оптимальности), возможных в условиях априорной неопределенности и рассмотренных в § 4.3, то есть действительно этот подход дает наилучшие в условиях априорной неопределенности правила решения. Состоятельность оценки апостериорного риска обеспечивается, если в условиях параметрической априорной неопределенности заменить неизвестные значения параметров 3. При параметрической априорной неопределенности процедура нахождения адаптивного байесова правила решения принципиально весьма проста: она сводится к замене в обычном байесовом правиле решения u = uo(x, Если при этом оценка 4. Если вместо требования равномерно наилучшего приближения принять требование наилучшего приближения в среднем с весом Естественно, что это правило решения может быть найдено совершенно точно с помощью обычной байесовой процедуры при любой 5. Во многих случаях оба правила решения (u0(x, |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 458. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 соответствуют различные совокупности параметров
соответствуют различные совокупности параметров 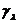 . Практически такая ситуация может возникнуть только в том случае, когда множество значений
. Практически такая ситуация может возникнуть только в том случае, когда множество значений  (
(  ). При этом апостериорный риск (6.5.8) может быть записан в виде
). При этом апостериорный риск (6.5.8) может быть записан в виде (6.5.18)
(6.5.18) - оценочное значение апостериорной вероятности k-ro дискретного значения
- оценочное значение апостериорной вероятности k-ro дискретного значения  (6.5.19)
(6.5.19)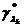 - оценка максимального правдоподобия параметров
- оценка максимального правдоподобия параметров 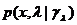 ;
; 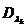 - значение матрицы
- значение матрицы 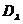 (6.5.6);
(6.5.6); 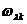 - значение функции
- значение функции  при
при 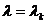 .
.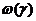 не задана, то, используя предполагавшееся ранее медленное изменение этой функции, можно оценить эти величины следующим образом:
не задана, то, используя предполагавшееся ранее медленное изменение этой функции, можно оценить эти величины следующим образом: (6.5.20)
(6.5.20) - эффективный объем области сосредоточения параметров
- эффективный объем области сосредоточения параметров 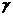 , входящих в распределение вероятности для х и
, входящих в распределение вероятности для х и  (х), найденной с использованием имеющихся данных наблюдения.
(х), найденной с использованием имеющихся данных наблюдения. ) к обычному байесову правилу решения, то соответствующее приближенно оптимальное правило решения u = u*(x) находится минимизацией усредненного по
) к обычному байесову правилу решения, то соответствующее приближенно оптимальное правило решения u = u*(x) находится минимизацией усредненного по  ) может быть найдено минимизацией состоятельных оценок апостериорного риска (6.5.8), (6.5.17), (6.5.18), для нахождения которых не требуется детального задания или вообще знания функции
) может быть найдено минимизацией состоятельных оценок апостериорного риска (6.5.8), (6.5.17), (6.5.18), для нахождения которых не требуется детального задания или вообще знания функции