
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
АДАПТИВНЫЙ БАЙЕСОВ ПОДХОД ПРИ ПАРАМЕТРИЧЕСКОЙ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ
Конкретные приложения рассматриваемых здесь методов в последующих главах будут применены в основном к задачам синтеза информационных систем в условиях параметрической априорной неопределенности, простейшим примером которых является первый из примеров § 6.1. Поэтому рассмотрим этот случай наиболее детально с доведением результатов до максимально возможной в условиях общей постановки задач степени конкретности. При параметрической априорной неопределенности (гл. 3) функция правдоподобия Р (х|l,
где р(x,l|g) - известная функция всех своих аргументов, удовлетворяющая обычным требованиям к плотности совместного распределения вероятности. Апостериорное распределение вероятности и апостериорный риск определяются обычными соотношениями
и в общем случае зависят от совокупности неизвестных параметров g. В частном случае, когда апостериорное распределение либо только значение u0 = u0(х, g). Для которого достигается минимум апостериорного риска, то есть удовлетворяется уравнение 
не зависит от g, априорная неопределенность не является существенной, а правило решения u0(х,g)=u0(х) является равномерно наилучшим правилом решения. Поэтому в любой конкретной задаче с априорной неопределенностью прежде всего следует проверить, решив уравнение (6.2.4), существует либо нет равномерно наилучшее решение. Если априорная неопределенность является существенной, то решение уравнения (6.2.4) зависит от g и представляет собой функцию u0(х,g), описывающую оптимальное байесово правило решения для известного значения g (при отсутствии априорной неопределенности). Поскольку истинное значение g неизвестно, то ни величина апостериорного риска (6.2.3), ни правило решения u0(х,g) не определены и необходимо применить адаптивный байесов подход, введя новую меру ожидаемых потерь - какую-либо оценку апостериорного риска, не зависящую от неизвестного значения g, Естественной оценкой величины R(u,x,g), обеспечивающей полное сохранение последующего байесова формализма, является
где
отличающееся от оптимального байесова правила только заменой g оценочным значением Таким образом, использование оценки апостериорного риска (6.2.5) позволяет не решать заново задачу минимизации ожидаемых потерь; структура правила решения остается такой же, как при отсутствии априорной неопределенности (известном значении g), а неопределенность правила решения устраняется заменой неизвестного значения g оценочным значением Адаптивное байесово правило решения (6.2.6) внешне выглядит очень привлекательным: оно универсально, обладает хорошими конструктивными качествами, так как позволяет просто взять готовое решение байесовой задачи и заменить в нем g на 1)какую именно оценку 2)удовлетворяет ли правило решения (6.2.6) какому-либо из рассмотренных в гл.4 принципов оптимальности или хотя бы является близким к наилучшему с точки зрения того или иного принципа предпочтения правилу. Если объем имеющихся данных наблюдения таков, что можно оценить значение g с высокой точностью, то ответ на первый из этих вопросов некритичен. В качестве При ограниченном объеме данных наблюдения выбор оценки
и сравним ее с величиной среднего риска для оптимального байесова решения u0(x,l) при том же значении g.
Для этого составим разность
где
Очевидно, что разность R( При этом R(
Величина DR(
Таким образом, с учетом (6.2.9) наилучшая оценка
относительно функции потерь
которая определяется из уравнения правдоподобия
или при отсутствии ограничений на область Г ={Аl, В} значений g из эквивалентного ему уравнения
где
- оператор градиента, ставящий в соответствие любой функции от g вектор-столбец частных производных этой функции по всем компонентам вектора g. При использовании оценки максимального правдоподобия g* = g*(x), определяемой уравнениями (6.2.15), (6.2.16), адаптивное байесово правило решения (6.2.6) принимает вид
и мы получаем замкнутую конструктивную процедуру нахождения правила решения в условиях априорной неопределенности, которое содержит следующие элементы: - отыскание оптимального байесова правила решения uo(x, g) для фиксированного значения g путем минимизации апостериорного риска R(u, x, g) из (6.2.3) (во многих случаях это означает просто взять готовое решение соответствующей задачи при отсутствии априорной неопределенности); - нахождение оценки максимального правдоподобия g* = g*(x) путем решения уравнений правдоподобия (6.2.15) или (6.2.16); - замена в оптимальном байесовом правиле решения u0(x, g) неизвестного значения g на его оценочное значение g* = g*(x). При слабых ограничениях на функцию потерь Указанные ограничения обычно выполняются, если множество значений 6.3. СЛУЧАИ, КОГДА МНОЖЕСТВА РЕШЕНИЙ u И ПАРАМЕТРОВlНЕПРЕРЫВНЫ
Прежде чем переходить к решению второго из поставленных в § 6.2 вопросов, рассмотрим важный частный случай, когда множества решений и u значений параметров l непрерывны и имеют одинаковую структуру. Как отмечалось выше, в этом случае решение и может быть интерпретировано как оценка параметра l, а правило решения u = u(x) ставит в соответствие каждому значению х значение этой оценки. Будем считать, что функция потерь является симметричной функцией разности u - l, тогда апостериорный риск
Пусть плотность совместного распределения вероятности
где
взятые со знаком минус матрицы, составленные из вторых производных логарифма плотности
где Из выражения для апостериорного риска (6.3.5) следует, что оптимальная байесова оценка
Действительно, благодаря свойствам функции потерь g(u - l) выражение (6.3.6) дифференцируемо по u под знаком интеграла, при этом Из выражения (6.3.6) следует, что оценка максимального правдоподобия параметра
Тем самым уравнение (6.3.3) дает полное решение задачи - оно определяет наилучшее в условиях априорной неопределенности решение задачи оценивания l и дает оценку максимального правдоподобия для параметра Покажем, что правило решения (6.3.8) удовлетворяет требованию (6.2.12) равномерно наилучшего приближения к оптимальному байесову решению с известным значением
Вычисляя значения апостериорного риска (6.3.5) при
где Величина разности средних рисков адаптивного и оптимального при известном
где для сокращения записи обозначено
Математическое ожидание матрицы Из выражения (6.3.10) видно, что задача нахождения минимаксной оценки |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 503. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
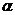 l) задается с точностью до совокупности неизвестных параметров
l) задается с точностью до совокупности неизвестных параметров  (6.2.1)
(6.2.1) (6.2.2)
(6.2.2) (6.2.3)
(6.2.3) (6.2.4)
(6.2.4) (6.2.5)
(6.2.5) =
=  (6.2.6)
(6.2.6) (6.2.7)
(6.2.7)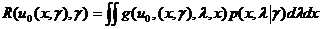 . (6.2.8)
. (6.2.8) (6.2.9)
(6.2.9) (6.2.10)
(6.2.10) (
(  (6.2.11)
(6.2.11) (6.2.12)
(6.2.12)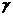 плотности распределения вероятности
плотности распределения вероятности (6.2.13)
(6.2.13) (6.2.14)
(6.2.14) (6.2.15)
(6.2.15)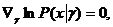 (6.2.16)
(6.2.16) (6.2.17)
(6.2.17) , (6.2.18)
, (6.2.18) непрерывно, а также в ряде других случаев. Мы не будем заниматься специально детальным анализом условий совпадения оценки максимального правдоподобия g*(х) с минимаксной оценкой go(x) определяемой из (6.2.12). Конечно, могут быть ситуации, когда y0(х) лучше, чем g*(x), в смысле точности приближения среднего риска правила решения u0(x, g0(х)) к среднему риску байесова правила u0(x, g), и, взяв действительно минимаксную оценку, можно было бы получить лучшие результаты, чем с оценкой максимального правдоподобия. Примером подобного рода является случай, когда значение g задает априорное распределение на дискретном множестве значений l, а данные наблюдения х относятся только к одному из возможных значений l. В этом и некоторых подобных случаях оптимальное значение g0(х) получается константой, не зависящей от х, что довольно очевидно заранее и существенно упрощает нахождение правила решения. Однако такие ситуации сравнительно редки, а сама оценка при условии единственности решения уравнения максимального правдоподобия, как уже неоднократно отмечалось, обладает следующими качествами: она обязательно совпадает с эффективной (имеющей наименьшее возможное рассеяние) оценкой, если последняя существует; с ростом объема данных наблюдения, по которым вычисляется оценка максимального правдоподобия, она сходится к истинному значению оцениваемого параметра и при этом является асимптотически нормальной и асимптотически эффективной. Имея в виду эти высокие достоинства, а также универсальность и относительную простоту метода максимального правдоподобия, благодаря которым могут быть разработаны стандартные процедуры нахождения оценки g*, можно в общем случае ограничиться оценками максимального правдоподобия, оставив попытки их улучшения для конкретных задач, где такая возможность имеется.
непрерывно, а также в ряде других случаев. Мы не будем заниматься специально детальным анализом условий совпадения оценки максимального правдоподобия g*(х) с минимаксной оценкой go(x) определяемой из (6.2.12). Конечно, могут быть ситуации, когда y0(х) лучше, чем g*(x), в смысле точности приближения среднего риска правила решения u0(x, g0(х)) к среднему риску байесова правила u0(x, g), и, взяв действительно минимаксную оценку, можно было бы получить лучшие результаты, чем с оценкой максимального правдоподобия. Примером подобного рода является случай, когда значение g задает априорное распределение на дискретном множестве значений l, а данные наблюдения х относятся только к одному из возможных значений l. В этом и некоторых подобных случаях оптимальное значение g0(х) получается константой, не зависящей от х, что довольно очевидно заранее и существенно упрощает нахождение правила решения. Однако такие ситуации сравнительно редки, а сама оценка при условии единственности решения уравнения максимального правдоподобия, как уже неоднократно отмечалось, обладает следующими качествами: она обязательно совпадает с эффективной (имеющей наименьшее возможное рассеяние) оценкой, если последняя существует; с ростом объема данных наблюдения, по которым вычисляется оценка максимального правдоподобия, она сходится к истинному значению оцениваемого параметра и при этом является асимптотически нормальной и асимптотически эффективной. Имея в виду эти высокие достоинства, а также универсальность и относительную простоту метода максимального правдоподобия, благодаря которым могут быть разработаны стандартные процедуры нахождения оценки g*, можно в общем случае ограничиться оценками максимального правдоподобия, оставив попытки их улучшения для конкретных задач, где такая возможность имеется. (6.3.1)
(6.3.1)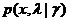 дважды дифференцируема по
дважды дифференцируема по  (6.3.2)
(6.3.2) ,
,  - решение уравнения
- решение уравнения (6.3.3)
(6.3.3) (6.3.4)
(6.3.4) ,
,  , которые подобно
, которые подобно  и
и  зависят только от х;
зависят только от х;  - оператор градиента по компонентам
- оператор градиента по компонентам  ;
;  ,
,  - операторы градиента, ставящие в соответствие той функции, на которую действуют такие операторы, вектор-строку частных производных этой функции по всем компонентам
- операторы градиента, ставящие в соответствие той функции, на которую действуют такие операторы, вектор-строку частных производных этой функции по всем компонентам  и
и  . Роль этих членов тем меньше, чем больше объем данных наблюдения х; по мере его увеличения совместное распределение вероятности
. Роль этих членов тем меньше, чем больше объем данных наблюдения х; по мере его увеличения совместное распределение вероятности  , (6.3.5)
, (6.3.5) , (6.3.6)
, (6.3.6) - как всегда матрица, обратная матрице
- как всегда матрица, обратная матрице  ;
;  - некоторая неотрицательная функция, зависящая только от х.
- некоторая неотрицательная функция, зависящая только от х. параметра
параметра 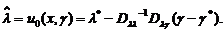 (6.3.7)
(6.3.7) - нечетная функция своего аргумента и, следовательно, при подстановке u = u0(x,
- нечетная функция своего аргумента и, следовательно, при подстановке u = u0(x,  обращается в нуль, то есть обеспечивается минимум апостериорного риска.
обращается в нуль, то есть обеспечивается минимум апостериорного риска. (6.3.8)
(6.3.8)
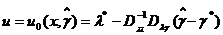 , где
, где  - какая либо оценка
- какая либо оценка  и беря их разность, получаем следующее выражение для функции
и беря их разность, получаем следующее выражение для функции (6.3.9)
(6.3.9) будет при этом равна
будет при этом равна (6.3.10)
(6.3.10)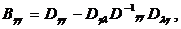 (6.3.11)
(6.3.11) представляет собой информационную матрицу Фишера для совокупности параметров g.
представляет собой информационную матрицу Фишера для совокупности параметров g.