
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Структурная оптимизация при случайных воздействиях ⇐ ПредыдущаяСтр 4 из 4 Оптимизация всегда производится с целью получения оптимальных значений некоторого критерия. Если структура системы выбрана, то оптимизация, как показано в § 5.7, проводится путем выбора значений параметров из условий оптимальности этого критерия. Однако оптимальное значение критерия всегда зависит не только от параметров системы, но и от её структуры. Поэтому более рациональным методом построения оптимальной системы является структурная оптимизация, при которой и структура, и параметры системы оказываются оптимальными. Если проектируемая система функционирует в условиях случайных воздействий, то её качество оценивается среднеквадратической ошибкой (СКО). Поэтому структурную оптимизацию САУ в этом случае целесообразно проводить путем минимизации СКО. В настоящее время существует два метода решения этой задачи: метод Н. Винера и метод аналитического конструирования оптимальных регуляторов (АКОР), независимо предложенный А.М. Лётовым и Р. Калманом. Метод Винера. В этом методе задача синтеза ставится так же, как и в рассмотренном выше методе параметрической оптимизации (см. § 5.7). Эта постановка приведена также на рис. 7.9, где оптимизируемая САУ представлена либо своей передаточной функцией W(p), либо своей импульсной переходной функцией w(t). Входные случайные воздействия Случайные сигналы Задача оптимизации заключается в определении физически реализуемой 
При решении задачи оптимизации в качестве условия физической реализуемости системы Н. Винером было принято следующее условие:
Для решения задачи при условии (7.57) записывается приведенная выше формула (5.60) для дисперсии СКО, где неизвестной считается вся функция
К сожалению, в большинстве случаев оригинальный метод Винера приводит к физически нереализуемой оптимальной
Эта функция удовлетворяет условию (7.57), но физические элементы, которые имели бы импульсные переходные функции такого типа, создать невозможно. Кроме того, САУ обычно содержат так называемую заданную часть – объект управления с исполнительными и измерительными устройствами. Объекты управления, как правило, описываются уравнениями в переменных состояния, уравнениями вход-выход типа (7.4) или передаточными функциями
где Обозначим Так как оптимальная передаточная функция системы всегда должна быть физически реализуемой, то она должна иметь параметр
где Таким образом, с учетом наличия заданной части (7.58) условие физической реализуемости оптимальной системы имеет вид (7.59). С тем, чтобы учесть это условие, в процедуре оптимизации Н. Винера в качестве критерия оптимальности выбирается следующий функционал:
где Второе слагаемое в (7.60) называется функционалом сложности, так как оно, помимо увеличения параметра Выбором значения
При этом неслучайные задающее воздействие
где В результате проведения оптимизации функционала (7.60) в соответствии с методикой Н. Винера также получается оптимальная передаточная функция При выполнении (7.61) передаточная функция После определения оптимальных значений всех коэффициентов передаточной функции
Описанная процедура синтеза оптимальных в смысле минимума СКО систем управления является аналитической. Поэтому на её основе могут быть разработаны различного рода программы для расчетов с помощью ПЭВМ. Пример 7.5. Синтезировать оптимальную следящую систему, если
а заданный объект управления описывается уравнением
Решение. В данном случае неслучайные составляющие отсутствуют, поэтому поли- номы
где Числитель
где Соотношения (7.63) и (7.64) позволяют найти оптимальную передаточную функцию системы следующего вида:
где Численное значение коэффициента Замкнутая система состоит из заданного объекта управления (7.62) и оптимального устройства управления, описываемого найденным уравнением типа (7.25) при Из выражения (7.65) следует, в частности, что если параметр С другой стороны, на основе выражения (7.65) можно заключить, что включение в оптимизируемый критерий (7.60) интеграла от производной импульсной переходной функции (функционала сложности) приводит к повышению порядка оптимальной системы, т.е. к повышению её сложности с одновременным увеличением её СКО. Другими словами, за физическую реализуемость оптимальных характеристик приходится «платить» повышенной СКО САУ. Однако, соотношение (7.61) позволяет синтезировать оптимальные системы минимальной сложности, т.е. системы с минимальным повышением СКО. Оптимизация методом АКОР. Метод АКОР позволяет решить ту же самую задачу определения оптимального устройства управления с учетом условий физической реализуемости, но на основе уравнений в переменных состояния:
Здесь Равенство (7.67) называется уравнением наблюдения. Здесь символом Отметим, что если уравнения (7.66), (7.67) включают математические модели детерминированных или случайных воздействий, то этот объект управления называется расширенным. Задача синтеза системы управления здесь заключается в выборе оптимального управления вида
Здесь Kор – матрица оптимального регулятора, которая и должна быть определена в результате решения задачи оптимизации. При этом обычно предполагается, что вектор выходных переменных y в (7.66), (7.67) является вектором сигналов ошибки, т.е.
Тогда матрица дисперсий ошибок
или
где Таким образом, дисперсию ошибки управления можно представить в виде квадратичной формы и найти оптимальное управление из условия минимума величины
где Q и R– матрицы коэффициентов, причем
Здесь матрица
где Интересно, что, несмотря на наличие белых шумов, приложенных к расширенному объекту управления (7.66), их характеристики никак не влияют на оптимальное управление (7.70). Что же касается цветных шумов, которые приложены к исходному объекту управления (см. рис. 7.9), то их свойства учитываются в уравнениях расширенного объекта, путем включения в (7.66) уравнений соответствующих формирующих фильтров. Соотношения (7.66) – (7.71) составляют содержание метода АКОР. Для решения уравнения Риккати (7.71) разработаны специальные программы, которые содержатся в системах математического обеспечения ЭВМ. Однако в случае объекта второго порядка это уравнение можно решить аналитически. Пример 7.6. Найти оптимальное управление скоростью двигателя, отклонения которой от заданного значения описывается следующими уравнениями:
Решение. Найдем сначала матрицу Q из уравнения Риккати (7.71) по приведенной выше формуле
Пусть
В данном случае порядок системы
По определению K – симметрическая матрица, т. е.
Если в этом матричном уравнении произвести все необходимые операции над матрицами в левой части и приравнять друг другу элементы матриц слева и справа, то получится система из трех уравнений относительно
Это управление минимизирует функционал Полученное оптимальное управление по состоянию (7.73) может быть реализовано только тогда, когда переменные состояния случае совокупность двух усилителей и сумматор. Оптимальное оценивание переменных состояния. Если измеряемая переменная объекта измеряется без ошибки, то в качестве переменных в оптимальном управлении (7.70) можно взять асимптотические оценки (см. § 3.7) переменных состояния объекта управления (7.66), (7.67). Однако обычно выходной сигнал измерительных приборов сопровождается шумом, как это видно из уравнения (7.67). Поэтому для получения оценок переменных состояния здесь целесообразнее применить наблюдатель, который бы наилучшим образом подавлял влияние этих шумов. Эту задачу и решает фильтр Калмана-Бьюси или оптимальный наблюдатель. Рассмотрим его уравнения. При этом, по-прежнему, будем предполагать, что объект описывается уравнениями (7.66) и (7.67), а белые шумы характеризуются матрицами дисперсий
Оптимальный наблюдатель строится так, чтобы след матрицы дисперсий сигнала ошибки оценивания
где Уравнение фильтра Калмана-Бьюси для объекта (7.66), (7.67) имеет вид
и, как видно, совпадает с уравнением обычного наблюдателя Калмана (см. § 3.7). Лишь матрица обратных связей L определяется здесь по-другому, а именно, по формуле
где P– решение матричного уравнения Риккати, которое в этом случае имеет вид
При наличии вектора оптимальных оценок оптимальное управление
Обратим внимание, что уравнение оптимального наблюдателя никак не связано с уравнением оптимального регулятора, т.е. задачи оптимального управления и оптимального оценивания в случае линейных систем решаются независимо друг от друга. Пример 7.7. Построить оптимальный наблюдатель (7.75) для оценивания переменных состояния двигателя, рассмотренного в предыдущем примере 7.6, при наличии случайного возмущающего момента
где Решение. В нашем случае матрицы
а уравнение Риккати (7.77), определяющее коэффициенты обратной связи наблюдателя, принимает вид
где
Решение приведённого уравнения Риккати дает значения:
Следовательно, уравнение фильтра Калмана-Бьюси (7.75) и управление по состояниям (7.78) с учетом (7.73) в данном случае имеют вид
Полученная система уравнений (7.81), (7.82), по существу, описывает оптимальный регулятор для объекта (7.79), (7.80), построенный методом АКОР или, как говорят иногда, путем оптимизации во временной области. Для сравнения, заметим, что при решении аналогичной задачи методом Н. Винера оптимизация проводится в частотной области. Структура оптимальных систем с наблюдателем. На основании изложенного выше можно заключить, что оптимальная система управления с оптимальным наблюдателем состояния имеет структуру, приведённую на рис. 7.10. Как видно, в этом случае система состоит из трех частей: собственно объекта управления, оптимального наблюдателя и формирователя оптимального управления. Наблюдатель и формирователь образуют оптимальный регулятор. Обратим внимание, что структура оптимального наблюдателя практически полностью совпадает со структурой расширенного объекта. Небольшое отличие заключается лишь в дополнительной обратной связи, определяемой матрицей L. Фактически для построения оптимальной системы (рис. 7.10) необходимо решить два уравнения Риккати (7.71) и (7.77). Удобнее всего это осуществляется с помощью программы LQG из пакета MATLAB, которая по заданным уравнениям (7.66), (7.67) расширенного объекта, критерию (7.69) и характеристикам (7.74) шумов вычисляет параметры непосредственно уравнений оптимального регулятора (7.75), (7.78). Для обращения к этой программе предварительно формируются вспомогательные матрицы |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 220. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  эталонной системы считается заданной.
эталонной системы считается заданной. так, чтобы дисперсия
так, чтобы дисперсия  случайного сигнала ошибки
случайного сигнала ошибки  была минимальной, т.е.
была минимальной, т.е.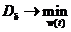 . (7.56)
. (7.56)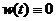 при
при  . (7.57)
. (7.57) . Далее путем вычисления первой вариации по
. Далее путем вычисления первой вариации по  или соответствующая ей импульсная переходная функция
или соответствующая ей импульсная переходная функция .
.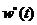 , так как последняя содержит
, так как последняя содержит  -функции, т.е. обычно имеет вид
-функции, т.е. обычно имеет вид .
.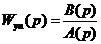 , (7.58)
, (7.58) .
. . Обычно
. Обычно  (например, чистый дифференциатор характеризуется значением
(например, чистый дифференциатор характеризуется значением  , но это не реальное звено, а лишь идеализация реального дифференцирующего элемента с
, но это не реальное звено, а лишь идеализация реального дифференцирующего элемента с  ).
). не только больше нуля, но даже больше
не только больше нуля, но даже больше  , так как для системы
, так как для системы , (7.59)
, (7.59) – аналогичный параметр устройства управления, которое будет добавлено к объекту для получения оптимальной системы управления.
– аналогичный параметр устройства управления, которое будет добавлено к объекту для получения оптимальной системы управления. , (7.60)
, (7.60)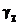 – неопределенный множитель Лагранжа,
– неопределенный множитель Лагранжа,  – порядок производной от импульсной переходной функции оптимизируемой САУ.
– порядок производной от импульсной переходной функции оптимизируемой САУ. системы, приводит к увеличению и порядка системы управления, т.е. её сложности. Подчеркнём, что в общем случае
системы, приводит к увеличению и порядка системы управления, т.е. её сложности. Подчеркнём, что в общем случае  – порядка производной в (7.60) можно всегда обеспечить выполнение условия (7.59) при заданных воздействиях
– порядка производной в (7.60) можно всегда обеспечить выполнение условия (7.59) при заданных воздействиях  ,
,  .
. и возмущение
и возмущение  задаются своими
задаются своими  -изображениями в виде полиномов
-изображениями в виде полиномов  и
и  соответственно. Поэтому в общем случае значение порядка
соответственно. Поэтому в общем случае значение порядка  , (7.61)
, (7.61)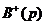 – полином, включающий только правые нули полинома
– полином, включающий только правые нули полинома  , находящегося в числителе передаточной функции объекта управления (7.58).
, находящегося в числителе передаточной функции объекта управления (7.58). , но зависящая от произвольно выбираемого коэффициента
, но зависящая от произвольно выбираемого коэффициента  выбирается из условия минимума СКО, т.е. из условия (7.56), а также с учетом различных конструктивных ограничений.
выбирается из условия минимума СКО, т.е. из условия (7.56), а также с учетом различных конструктивных ограничений. , по ней и по передаточной функции заданной части (7.58) находятся уравнения соответствующего оптимального устройства управления типа (7.25) при
, по ней и по передаточной функции заданной части (7.58) находятся уравнения соответствующего оптимального устройства управления типа (7.25) при  ,
,  с учетом следующих условий физической реализуемости:
с учетом следующих условий физической реализуемости: ,
,  .
. ,
,  ,
,  ,
, . (7.62)
. (7.62) и при
и при  по (7.61) имеем
по (7.61) имеем  . Знаменатель передаточной функции
. Знаменатель передаточной функции  , (7.63)
, (7.63) – полином, включающий только левые, а
– полином, включающий только левые, а  – только правые нули полинома в левой части (7.63), соответственно.
– только правые нули полинома в левой части (7.63), соответственно. , (7.64)
, (7.64) и
и  – неизвестные константа и полином второго порядка.
– неизвестные константа и полином второго порядка. , (7.65)
, (7.65)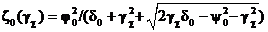 ,
, 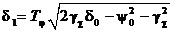 ,
,  .
. выбирается по условию минимума СКО с учетом допустимого увеличения коэффициентов передачи соответствующего оптимального устройства управления типа (7.25). Уравнения последнего определяются путем приравнивания передаточной функции замкнутой системы и правой части выражения (7.65) с учетом указанных выше условий физической реализуемости.
выбирается по условию минимума СКО с учетом допустимого увеличения коэффициентов передачи соответствующего оптимального устройства управления типа (7.25). Уравнения последнего определяются путем приравнивания передаточной функции замкнутой системы и правой части выражения (7.65) с учетом указанных выше условий физической реализуемости. , то параметр
, то параметр  , (7.66)
, (7.66) . (7.67)
. (7.67) ,
,  ,
,  – матрицы уравнений заданной части системы. Эти уравнения записываются с учетом математических моделей в переменных состояния объекта управления (7.58), неслучайных воздействий
– матрицы уравнений заданной части системы. Эти уравнения записываются с учетом математических моделей в переменных состояния объекта управления (7.58), неслучайных воздействий 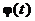 и
и  . Поэтому
. Поэтому  – обязательно белый шум, возбуждающий формирующие фильтры “цветных” случайных воздействий. В общем случае шум
– обязательно белый шум, возбуждающий формирующие фильтры “цветных” случайных воздействий. В общем случае шум  обозначены шумы измерительных устройств. Эти шумы называются шумами наблюдений, и обычно предполагается, что они являются белыми, причем всегда дисперсия
обозначены шумы измерительных устройств. Эти шумы называются шумами наблюдений, и обычно предполагается, что они являются белыми, причем всегда дисперсия  .
.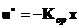 . (7.68)
. (7.68) .
.

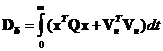 ,
, – симметрическая матрица.
– симметрическая матрица. . Но, как и в случае фильтра Винера, получаемое таким путём решение оказывается физически нереализуемым. Поэтому для обеспечения реализуемости А.М. Лётов и Р. Калман в конце 50-х годов двадцатого века независимо друг от друга предложили искать управление (7.68) путем минимизации функционала вида
. Но, как и в случае фильтра Винера, получаемое таким путём решение оказывается физически нереализуемым. Поэтому для обеспечения реализуемости А.М. Лётов и Р. Калман в конце 50-х годов двадцатого века независимо друг от друга предложили искать управление (7.68) путем минимизации функционала вида , (7.69)
, (7.69) , а
, а  . Выбором коэффициентов матриц Q и Rобеспечивается желаемый характер переходных процессов оптимальной системы управления. Оптимальное управление, при котором достигается минимум функционала (7.69), является управлением по состоянию и определяется выражением
. Выбором коэффициентов матриц Q и Rобеспечивается желаемый характер переходных процессов оптимальной системы управления. Оптимальное управление, при котором достигается минимум функционала (7.69), является управлением по состоянию и определяется выражением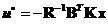 . (7.70)
. (7.70) является решением нелинейного матричного уравнения Риккати
является решением нелинейного матричного уравнения Риккати , (7.71)
, (7.71)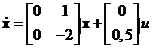 ,
,  .
. .
. . Тогда, подставляя в (7.69) матрицы
. Тогда, подставляя в (7.69) матрицы  и
и  , будем иметь
, будем иметь
 . (7.72)
. (7.72) , поэтому решение уравнения Риккати (7.71) – матрица K имеет вид
, поэтому решение уравнения Риккати (7.71) – матрица K имеет вид .
. . Поэтому в данном случае из (7.71) вытекает уравнение
. Поэтому в данном случае из (7.71) вытекает уравнение
 .
. . Решение этих уравнений даёт следующие значения:
. Решение этих уравнений даёт следующие значения: 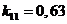 ;
;  ;
;  . Подставляя выражения для матриц
. Подставляя выражения для матриц  . (7.73)
. (7.73)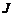 (7.72). ■
(7.72). ■ ,
,  могут быть измерены. Другими словами в тех случаях, когда могут быть получены физические величины, пропорциональные этим переменным состояния, и которые могут быть введены в регулятор, представляющий в данном
могут быть измерены. Другими словами в тех случаях, когда могут быть получены физические величины, пропорциональные этим переменным состояния, и которые могут быть введены в регулятор, представляющий в данном ,
,  . (7.74)
. (7.74) вектора переменных состояния x расширенного объекта(7.66) и (7.67) был минимальным, т.е. если
вектора переменных состояния x расширенного объекта(7.66) и (7.67) был минимальным, т.е. если  , то
, то ,
, – след матрицы
– след матрицы  .
. , (7.75)
, (7.75) , (7.76)
, (7.76)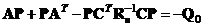 . (7.77)
. (7.77) вектора переменных состояния x
вектора переменных состояния x (7.70) определяется выражением
(7.70) определяется выражением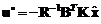 . (7.78)
. (7.78) и белого шума измерений отклонения скорости от заданного значения. Уравнения заданной части системы имеют вид
и белого шума измерений отклонения скорости от заданного значения. Уравнения заданной части системы имеют вид , (7.79)
, (7.79) (7.80)
(7.80) – случайный белый шум с дисперсией
– случайный белый шум с дисперсией  ;
; 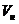 – случайная ошибка измерения отклонений скорости двигателя, которая является случайным процессом типа белого шума с дисперсией
– случайная ошибка измерения отклонений скорости двигателя, которая является случайным процессом типа белого шума с дисперсией  .
. и
и  (7.74) равны
(7.74) равны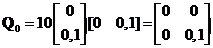 ,
,  ,
,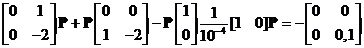 ,
, .
. ;
;  ;
;  . Подставляя в (7.76) матрицы
. Подставляя в (7.76) матрицы  ,
,  и величину
и величину 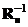 , получим
, получим .
. , (7.81)
, (7.81) . ■ (7.82)
. ■ (7.82)