
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет модального управления в общем случаеЕсли уравнения объекта (7.1), (7.2) имеют не КУФ (7.8), а любую другую форму, то для расчета параметров модального управления можно предварительно привести заданные уравнения объекта к КУФ. Как известно, это приведение осуществляется с помощью преобразования
Здесь U – матрица управляемости, определяемая выражением (3.3) при В = b, а Однако для того, чтобы уравнения общего вида объекта (7.1), (7.2) можно было привести к КУФ, необходимо, чтобы detU¹ 0. Таким образом, задачу расчета параметров модального управления (произвольного размещения всех полюсов системы) в случае объекта общего вида можно решить только тогда, когда объект является полностью управляемым. Алгоритм решения задачи в этом случае состоит из следующих шагов: 1. Для заданного объекта (7.1), (7.2) найти матрицу управляемости U (3.3). 2. Если detU¹ 0, то перейти к пункту 3, в противном случае задача не имеет ре- шения. 3. Найти det(pE – А) (7.9) и его коэффициенты 4. Построить по (7.14) матрицу 5. Построить по (7.11) полином 6. Найти вспомогательный вектор 7. Перейти к исходной системе координат, полагая 8. Для проверки найти матрицу Пример синтеза модального управления в общем случае приводится в следующем параграфе 
Инвариантность нулей систем с модальным управлением Если замкнутая система управления синтезирована на основе управления по состоянию, то она обладает одним интересным свойством, которое позволяет, в частности, назначать желаемые полюсы системы с учётом требуемого порядка астатизма. Предположим, для объекта управления (7.1), (7.2) общего вида найдены передаточные функции
где полином соответствии с полиномом Утверждение. Передаточная функция по задающему воздействию системы с управлением по состоянию (7.4) имеет тот же числитель, что и передаточная функция по управлению (7.15) исходного объекта, т.е.
В то же время передаточная функция системы по возмущению имеет в числителе полином, отличающийся от полинома в числителе передаточной функции (7.16) объекта по тому же возмущению. Другими словами, при назначении желаемых полюсов замкнутой системы коэффициенты числителя передаточной функции (7.17) являются известными величинами. Это позволяет назначить желаемые полюсы замкнутой, синтезируемой системы, например, так, чтобы выполнялись условия (5.41) при Если переменные состояния объекта управления (7.1), (7.2) недоступны измерению, то реализация управления по состоянию осуществляется с помощью наблюдателей. Для этой цели используется либо наблюдатель полного порядка (наблюдатель Калмана), либо наблюдатель пониженного порядка (наблюдатель Луенбергера). Наблюдатель Калмана (см. § 3.7) формирует вектор оценок
Здесь Из выражения (7.19) следует, что и в случае применения наблюдателя приведённое выше утверждение остается справедливым, т.е. числитель передаточной функции по задающему воздействию системы с устройством управления, в котором используется наблюдатель, и реализуется управление (7.4), также совпадает с числителем передаточной функции по управлению исходного объекта. Таким образом, если система (7.5) синтезирована на основе управления по состоянию (7.4), то нули её передаточной функции по задающему воздействию (7.17) или (7.19) не зависят от параметров управления по состоянию, т.е. они инвариантны к управлению по состоянию (7.4). Так как модальное управление является частным случаем управления по состоянию, то системы с модальным управлением также обладают указанным свойством инвариантности. С другой стороны, на основе выражения (7.19) можно заключить, что динамика наблюдателя не влияет на характер переходной функции по задающему воздействию замкнутой системы. Она полностью определяется нулями передаточной функции по управлению объекта и полюсами, назначенными при расчете модального управления. Это заключение составляет содержание так называемой теоремы разделения, которая справедлива в линейном случае. Пример 7.2. Предположим, объект управления задан уравнениями
причём имеется возможность выбирать значения параметров k и T. Найти модальное управление так, чтобы замкнутая система имела второй порядок астатизма, время регулирования не более 3,5 секунд, а перерегулирование не более 10 %. При этом измеряются только y и отклонение Решение. Форма заданных уравнений не соответствует канонической управляемой. Поэтому в соответствии с алгоритмом, изложенным в § 7.3, найдем матрицу управляемости и её определитель. Имеем
Следовательно, задача имеет решение. Далее находим
Для выбора желаемых значений коэффициентов
Следовательно, Далее в соответствии с пунктом 6 применяемого алгоритма, находим коэффициенты вспомогательного вектора: Так как по условию задачи переменные состояния недоступны измерению, то необходимо, как отмечалось выше, синтезировать наблюдатель. Следуя методике, изложенной в § 3.8, найдем для объекта (7.20) матрицы:
Полюсы наблюдателя примем равными:
Наконец, заменяя в полученном выражении для управления u переменные состояния
Итак, синтезированное УУ описывается уравнениями (7.22) и (7.23), а замкнутая система – совокупностью уравнений (7.20), (7.22) и (7.23). Входными величинами УУ являются ε и y. Переходная функция синтезированной системы и её реакция на линейное воздействие Синтез инвариантных систем управления Инвариантные системы управления (см. § 5.6) обладают высокими показателями качества как в переходном, так и в установившемся режиме. Поэтому на практике чаще всего стремятся применять системы управления именно этого типа. Рассмотрим здесь методику синтеза инвариантных систем на основе управления по выходу и воздействиям (см. главу 8). Объект управления может быть задан как уравнениями в переменных состояния, так и уравнением вход-выход
где m – общее число возмущений, приложенных к объекту управления. Остальные обозначения те же, что и выше. В общем случае, уравнение устройства управления, реализующего управление по выходу и по воздействиям, в операторной форме имеет следующий вид:
Здесь R(p), Q(p), N(p), L(p) и Pi(p) – некоторые полиномы, а индекс i принимает значения, соответствующие лишь тем приложенным к объекту управления (7.24) возмущениям Задача синтеза инвариантной САУ при заданном объекте управления сводится к определению степеней и коэффициентов всех полиномов из уравнения (7.25). При этом, помимо требований к качеству системы, должны быть выполнены следующие условия физической реализуемости устройства управления (7.25):
Методика синтеза инвариантных САУ включает следующие этапы: 1. Составляется уравнение замкнутой системы (7.24), (7.25) относительно сигнала ошибки (см. § 5.1) с учетом влияния всех воздействий. 2. Проверяется возможность удовлетворения условий абсолютной инвариантности (см. § 5.6). Обычно эти условия могут быть удовлетворены выбором параметров устройства управления (7.25) относительно лишь некоторых воздействий. 3. По отношению к остальным воздействиям ищется возможность удовлетворения условиям селективной инвариантности и выбирается соответствующий вид полиномов из уравнения (7.25). 4. Выбираются порядок системы и значения параметров устройства управления (7.25), при которых обеспечивается устойчивость системы, и выполняются условия (7.26). 5. Определяются значения параметров устройства управления (7.25), при которых обеспечивается выполнение условий абсолютной и селективной инвариантности по тем воздействиям, по которым она достигается с учетом условий (7.26). Отметим, в частности, что в тех случаях, когда объект управления является минимально-фазовым и число его нулей передачи по управлению равно порядку объекта, т.е. когда полином B(p) в уравнении объекта (7.24) удовлетворяет условиям
где Рассмотрим примеры синтеза инвариантных систем. Пример 7.3. Для объекта управления, который описывается уравнениями
синтезировать абсолютно инвариантную систему к задающему воздействию g и неизмеряемому возмущению f. Физически реализуемое УУ (7.25) может иметь передаточные функции с одинаковыми степенями полиномов числителя и знаменателя. Решение. Переходя к решению задачи, прежде всего, найдем полиномы из уравнения (7.24) данного объекта: В соответствии с изложенной методикой запишем уравнение вход-выход замкнутой системы (7.28), (7.25), относительно отклонения
где обозначено
Из уравнения (7.29) и выражения (7.31) непосредственно следует, что условия абсолютной инвариантности рассматриваемой системы по отношению к возмущению f и к задающему воздействию g выполняются, например, при Подставляя выбранные полиномы R(p) и Q(p) в уравнение (7.25) с учётом условий
а его структурная схема приведена на рис. 7.4. Полученное УУ (7.33) имеет характеристический полином равный нулю, и поэтому иногда называется «вырожденным» или «сингулярным». Кроме того, оно содержит усилитель с Ky = 1 (рис. 7.4), охваченный положительной единичной обратной связью. Этот усилитель, как и всё УУ, является неустойчивым в разомкнутом состоянии. В замкнутой системе УУ охватывается отрицательными обратными связями (через объект управления), что и обеспечивает устойчивость и робастность абсолютно инвариантной системы управления. Для исследования полученной системы объединим уравнения (7.33) и (7.28). В результате получим систему уравнений
Нетрудно проверить, что эти уравнения замкнутой системы удовлетворяют всем приведённым выше условиям абсолютной инвариантности. Например, вычисляя величины Если промоделировать систему уравнений (7.34), (7.35) при задающем воздействии g(t) = 1(t), векторе начальных условий х0 = [1 0,5 2 1,5] и возмущении f(t) = 3 sin 5t, которое возникает при t = 3 и исчезает при t = 7 c, то переменные системы будут изменяться, как показано на рис. 7.5,б – рис. 7.7. На рис. 7.5,а приведён график изменения возмущения f(t), а на рис. 7.5,б – управляемой переменной y(t). Как видно из этих графиков, переходные процессы по управляемой переменной y(t) вызываются только ненулевыми начальными условиями. Возникновение или исчезновение возмущения f(t) на поведении управляемой переменной y(t) совершенно не сказывается. Это и свидетельствует об абсолютной инвариантности синтезированной системы к этому возмущению. Аналогично, на рис. 7.6,а приведены графики изменения переменных состояния объекта (7.28), а на рис. 7.6,б – УУ. Они свидетельствуют, что переменные х1(t) и х2(t) объекта изменяются в зависимости от возмущения f(t), а переменные Из приведённых графиков следует, что в абсолютно инвариантных системах происходит как бы «отключение» на сигнальном уровне управляемой переменной и ошибки системы от состояния объекта, к которому приложено возмущение, и «подключение» их к состоянию УУ, на которое возмущение не действует. Это «отключение» осуществляется путём формирования такого сигнала управления u(t), при котором осуществляется полная компенсация влияния воздействий на ошибку системы. Это хорошо видно из графиков изменения управления u(t) и возмущения f(t), приведенных на рис. 7.7 и на рис. 7.5,а. На УУ (7.33) возмущение f(t) непосредственно не действует. Поэтому, сравнивая рис. 7.5,а и рис. 7.7, можно заключить, что вырожденное УУ абсолютно инвариантной к неизмеряемому возмущению системы является «генератором» сигнала, подобного действующему возмущению. Условиям (7.27) удовлетворяют лишь небольшое число объектов управления. Большинство из них этим условиям не удовлетворяют. Поэтому абсолютная инвариантность чаще всего обеспечивается лишь по отношению к измеряемым возмущениям, т.е. в соответствии с принципом двухканальности Б.Н. Петрова. По отношению к неизмеряемым возмущениям чаще всего обеспечивается селективная инвариантность. Пример 7.4. Найти параметры устройства управления (7.25), обеспечивающего инвариантность следящей системы к задающему Уравнение объекта управления в операторной форме
Решение. В данном случае доступны измерению
Далее, поскольку система следящая, то сигнал ошибки
Найдем u из уравнения (7.37) с учётом замены
и подставим в (7.38). В результате будем иметь
Умножим обе части этого равенства на полином
где Изучая, в соответствии с пунктом 2 приведённого выше алгоритма синтеза, возможность достижения абсолютной инвариантности в рассматриваемой системе, отмечаем, что абсолютная инвариантность по отношению к С другой стороны, селективная инвариантность может быть достигнута по отношению ко всем воздействиям, если известны их В связи с этим будем искать устройство управления, исходя из следующих требований к качеству синтезируемой в данном примере системы управления: · селективная инвариантность к воздействию f2 ; · абсолютная инвариантность к воздействию f1; · астатизм первого порядка по отношению к задающему воздействию g , так как информации о его спектре нет; · устойчивость; · время регулирования Перейдем к определению детальной структуры и параметров устройства управления, обеспечивающего указанные требования.
Здесь Условие (5.50) абсолютной инвариантности проектируемой системы к воздействию f1 в соответствии с уравнением (7.39) имеет вид
где
откуда полином
В рассматриваемом случае полином A(p) = p(2p+1), т.е. объект управления содержит “чистый” интегратор, поэтому в соответствии с уравнением (7.39) для обеспечения первого порядка астатизма к задающему воздействию g достаточно выбрать Перейдём к обеспечению устойчивости системы. Согласно (7.39), характеристический полином системы с учетом полученного выражения (7.41) для
или
где Прежде всего, отметим, что выбор полинома R(p) по условию абсолютной инвариантности к воздействию f1 привел к тому, что полином (p + 10), являющийся нормированным полиномом B(p)при управлении u в уравнении объекта (7.36), оказался множителем характеристического полинома (7.44) синтезируемой системы. Замечание. Если объект (7.24) является неминимально-фазовым (в этом случае полином B(p) будет иметь «правые» нули), то абсолютную инвариантность к возмущению fi невозможно обеспечить даже при наличии двух каналов измерения. Возвращаясь к обеспечению устойчивости системы, будем считать, что характеристический полином системы
решение которого определяет искомые полиномы Чтобы задать полином
а число неизвестных – суммарному числу коэффициентов полиномов
Для разрешимости указанной системы, прежде всего, необходимо, чтобы число уравнений было не больше числа неизвестных. Из условия Если
Составленная указанным выше способом система, соответствующая уравнению (7.45) при
имеет следующий вид:
Здесь в первых четырех (l + 1) столбцах матрицы системы стоит 0,1 – коэффициент, на который в уравнении (7.45) умножается полином В левой части системы алгебраических уравнений (7.48) в том же порядке стоят
Знаменатель этой дроби равен полиному Из уравнений (7.36) и (7.37) можно вывести, что числитель передаточной функции замкнутой системы Таким образом, согласно (7.37), искомое УУ описывается уравнением
Записав с помощью уравнений (7.36) и (7.49) уравнение (7.39), можно убедиться, что синтезированная система удовлетворяет всем указанным выше требованиям. ■ Реализация устройства управления селективно инвариантных систем. Для реализации синтезированного УУ от уравнения (7.49) переходят к его уравнениям в переменных состояния, по которым либо составляется схема УУ на операционных усилителях, либо разрабатывается программа для микропроцессора, который будет вычислять дискретные значения управления u по измеренным значениям величин y, g и f1. Рассмотрим некоторые особенности реализации УУ для систем с селективной инвариантностью. В соответствии с условиями селективной инвариантности (5.55) или (5.56) для того, чтобы система обладала этим свойством по отношению к некоторому воздействию необходимо, чтобы её передаточная функция по ошибке, вызванной данным воздействием, содержала в качестве множителя полином, равный Принцип внутренней модели. Система обладает селективной инвариантностью к некоторому воздействию, если она явно содержит спектральную модель данного воздействия, т.е. структуру, способную генерировать сигнал, совпадающий по форме с данным воздействием. Этот принцип, в частности, подтверждается тем, что, например, для достижения астатизма второго порядка к некоторому задающему воздействию необходимо наличие в прямой цепи системы двух чистых интеграторов (см. § 5.5). С другой стороны, последовательное соединение двух чистых интеграторов является спектральной моделью линейного воздействия, так как при не нулевых начальных условиях на выходе второго интегратора формируется линейный сигнал. Функционирование селективно инвариантной системы, в которой реализована спектральная модель некоторого воздействия, протекает следующим образом. При отсутствии соответствующего внешнего воздействия спектральная модель не активна и не генерирует незатухающих сигналов, поскольку система устойчива. Однако, как только данное внешнее воздействие начинает влиять на систему, его спектральная модель начинает генерировать сигнал, совпадающий по форме с этим воздействием. В течение переходного процесса на интеграторах модели устанавливаются такие начальные значения, при которых она генерирует сигнал, полностью компенсирующий влияние воздействия на управляемую переменную системы в установившемся режиме. Когда влияние воздействия прекращается, в системе снова возникает переходный процесс, в течение которого внутренняя спектральная модель снова становится не активной. При реализации УУ селективно инвариантной системы для формирования спектральных моделей необходимо уравнения УУ представлять в виде нескольких подсистем уравнений в переменных состояния. Каждое из Покажем соответствующую методику на примере устройства управления, описываемого уравнением (7.49). С этой целью, полагая для упрощения схемы
Отсюда следует равенство Поскольку полином
Заметим, что коэффициенты числителей дробей в левой части (7.51) и (7.52) определяются решением системы уравнений
при Равенства (7.51) и (7.52) позволяют уравнение (7.50) заменить эквивалентной системой уравнений:
По выражениям (7.53) – (7.55) записываются соответствующие уравнения устройства управления в переменных состояния. В данном случае оно состоит из двух блоков, для формирования сигналов
Этим уравнениям соответствует структурная схема синтезированного устройства управления, приведённая на рис. 7.8. Элементы схемы на рис. 7.8, которые описываются уравнениями с вектором состояния В заключение этого параграфа отметим, что в общем случае условия разрешимости задачи синтеза инвариантных систем управления определяются как свойствами объекта управления, так и свойствами воздействий приложенных к нему.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 308. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , где матрица
, где матрица . (7.14)
. (7.14) -матрица М по-прежнему определяется выражением (3.43) с использованием коэффициентов ai характеристического полинома (7.9) системной матрицы А из уравнения объекта (7.1).
-матрица М по-прежнему определяется выражением (3.43) с использованием коэффициентов ai характеристического полинома (7.9) системной матрицы А из уравнения объекта (7.1).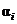 ,
,  .
. и обратную к ней
и обратную к ней  .
.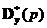 и найти
и найти  ,
, 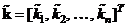 по (7.12), т.е. в соответствии с равенствами
по (7.12), т.е. в соответствии с равенствами  ,
,  .
. .
. , а затем коэффициенты её характеристического полинома. При безошибочных расчетах коэффициенты полученного полинома совпадают с коэффициентами
, а затем коэффициенты её характеристического полинома. При безошибочных расчетах коэффициенты полученного полинома совпадают с коэффициентами  , (7.15)
, (7.15) , (7.16)
, (7.16) , полином
, полином  , а полином
, а полином 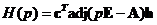 . Затем было найдено управление по состоянию
. Затем было найдено управление по состоянию 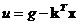 (7.4) в
(7.4) в , что привело к образованию замкнутой системы (7.5).
, что привело к образованию замкнутой системы (7.5). . ■ (7.17)
. ■ (7.17) (7.18)
(7.18) . В результате замкнутая система с модальным управлением будет обладать
. В результате замкнутая система с модальным управлением будет обладать  порядком астатизма по задающему воздействию.
порядком астатизма по задающему воздействию. , которым заменяется в управлении u (7.4) вектор х . В результате образуется замкнутая система с управлением по состоянию, состоящая из заданного объекта (7.1), (7.2), наблюдателя (3.30) и формирователя управления
, которым заменяется в управлении u (7.4) вектор х . В результате образуется замкнутая система с управлением по состоянию, состоящая из заданного объекта (7.1), (7.2), наблюдателя (3.30) и формирователя управления  . Оказывается, передаточную функцию этой системы по задающему воздействию можно всегда представить в виде
. Оказывается, передаточную функцию этой системы по задающему воздействию можно всегда представить в виде . (7.19)
. (7.19) – характеристический полином наблюдателя.
– характеристический полином наблюдателя. ,
,  , (7.20)
, (7.20)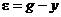 .
. ,
,  .
. ,
,  и матрицы
и матрицы ,
,  ,
,  .
. полинома
полинома  (7.11) воспользуемся методом стандартных передаточных функций (см. § 6.4). По заданным значениям
(7.11) воспользуемся методом стандартных передаточных функций (см. § 6.4). По заданным значениям  ,
,  и
и 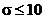 % из табл. 6.1 находим значения коэффициентов
% из табл. 6.1 находим значения коэффициентов  ,
,  ,
,  ,
,  , а также время
, а также время 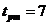 с. По формуле (6.14), полагая
с. По формуле (6.14), полагая  , получим
, получим  . Таким образом, в соответствии с выражением (6.13), желаемая передаточная функция замкнутой системы
. Таким образом, в соответствии с выражением (6.13), желаемая передаточная функция замкнутой системы . (7.21)
. (7.21) ,
,  ,
,  ,
,  . Так как преобразование
. Так как преобразование  , согласно (7.15) являются коэффициентами передаточной функции объекта по управлению. Поэтому, учитывая свойство инвариантности нулей систем с модальным управлением из (7.21), выводим равенства, определяющие варьируемые параметры объекта:
, согласно (7.15) являются коэффициентами передаточной функции объекта по управлению. Поэтому, учитывая свойство инвариантности нулей систем с модальным управлением из (7.21), выводим равенства, определяющие варьируемые параметры объекта: 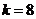 ,
,  ; отсюда
; отсюда  с.
с. ,
,  ,
,  , а переходя к исходным переменным, получим искомое модальное управление
, а переходя к исходным переменным, получим искомое модальное управление  .
. ,
,  .
. ,
,  ,
,  , что приводит к желаемому полиному наблюдателя
, что приводит к желаемому полиному наблюдателя  , векторам
, векторам  и
и  . Подставляя заданные и найденные (с округлением) векторы и матрицу в равенство (3.30), получим уравнение наблюдателя
. Подставляя заданные и найденные (с округлением) векторы и матрицу в равенство (3.30), получим уравнение наблюдателя . (7.22)
. (7.22)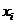 их оценками
их оценками  и полагая
и полагая  , будем иметь
, будем иметь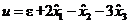 . (7.23)
. (7.23) приведены на рис. 7.3. Они получены в среде MATLAB. Как видно, синтезированная система имеет требуемые показатели качества. ■
приведены на рис. 7.3. Они получены в среде MATLAB. Как видно, синтезированная система имеет требуемые показатели качества. ■ , (7.24)
, (7.24) . (7.25)
. (7.25) , которые доступны измерению с помощью датчиков.
, которые доступны измерению с помощью датчиков. ,
,  ,
, ,
,  . (7.26)
. (7.26) ,
,  ,
,  , (7.27)
, (7.27) – корни полинома B(p), управление по выходу и по воздействиям (7.25) позволяет по указанной методике синтезировать устройство управления (УУ), обеспечивающее абсолютную инвариантность системы к задающему воздействию и неизмеряемым возмущениям.
– корни полинома B(p), управление по выходу и по воздействиям (7.25) позволяет по указанной методике синтезировать устройство управления (УУ), обеспечивающее абсолютную инвариантность системы к задающему воздействию и неизмеряемым возмущениям. ,
,  , (7.28)
, (7.28) ,
,  ,
,  . Условия (7.27), очевидно выполняются, т.е. задача синтеза имеет решение.
. Условия (7.27), очевидно выполняются, т.е. задача синтеза имеет решение.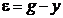 :
: , (7.29)
, (7.29)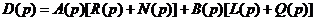 , (7.30)
, (7.30) , (7.31)
, (7.31) . (7.32)
. (7.32) и
и  . При этих условиях характеристический полином (7.30) замкнутой системы равен сумме двух полиномов: полинома
. При этих условиях характеристический полином (7.30) замкнутой системы равен сумме двух полиномов: полинома  , все коэффициенты которого теоретически равны нулю, и полинома
, все коэффициенты которого теоретически равны нулю, и полинома  . Поэтому для того, чтобы система была устойчивой, а УУ реализуемым, примем
. Поэтому для того, чтобы система была устойчивой, а УУ реализуемым, примем  , а
, а  . При этом, поскольку объект удовлетворяет условию (7.27), в характеристическом полиноме системы не будут появляться нулевые коэффициенты, так как
. При этом, поскольку объект удовлетворяет условию (7.27), в характеристическом полиноме системы не будут появляться нулевые коэффициенты, так как  .
.  и
и  . Соответствующие уравнения УУ в переменных состояния имеют вид
. Соответствующие уравнения УУ в переменных состояния имеют вид ,
,  , (7.33)
, (7.33) , (7.34)
, (7.34) ,
, 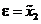 ,
,  . (7.35)
. (7.35) ,
, 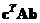 ,
,  ,
,  , а также
, а также  ,
,  ,
,  ,
, 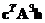 , где A, b, h и c – соответствующие матрица и векторы из уравнений (7.34), (7.35), найдём, что все эти величины равны нулю.
, где A, b, h и c – соответствующие матрица и векторы из уравнений (7.34), (7.35), найдём, что все эти величины равны нулю. и
и  УУ не зависят от этого возмущения. Таким образом, условия абсолютной инвариантности приводят к тому, что управляемая переменная системы зависит от переменных состояния УУ и задающего воздействия и не зависит от переменных состояния объекта управления и возмущений.
УУ не зависят от этого возмущения. Таким образом, условия абсолютной инвариантности приводят к тому, что управляемая переменная системы зависит от переменных состояния УУ и задающего воздействия и не зависит от переменных состояния объекта управления и возмущений. и двум возмущающим воздействиям
и двум возмущающим воздействиям  и
и  , а также время регулирования 2 с. При этом известно, что выход
, а также время регулирования 2 с. При этом известно, что выход  и воздействия
и воздействия 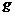 и
и  доступны измерению, а
доступны измерению, а  рад/с.
рад/с. . (7.36)
. (7.36)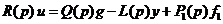 . (7.37)
. (7.37)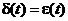 , поэтому запишем уравнение системы (7.36), (7.37) относительно отклонения
, поэтому запишем уравнение системы (7.36), (7.37) относительно отклонения  . С этой целью умножим обе части равенства
. С этой целью умножим обе части равенства 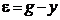 на полином
на полином  и учтём уравнение объекта (7.36). В результате будем иметь
и учтём уравнение объекта (7.36). В результате будем иметь
 . (7.38)
. (7.38)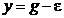
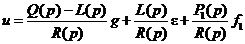

 .
. и приведём подобные члены:
и приведём подобные члены:

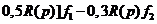 , (7.39)
, (7.39)  . Итак, равенство (7.39) – это искомое уравнение проектируемой системы, записанное относительно отклонения ε.
. Итак, равенство (7.39) – это искомое уравнение проектируемой системы, записанное относительно отклонения ε.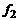 недостижима (так как нельзя взять полином R(p)равным нулю, а других возможностей для указанной цели нет). Абсолютная инвариантность к измеряемому возмущению f1 достижима (так как есть возможность выбора полинома P1(p)), а по отношению к задающему воздействию g – недостижима, так как заданный объект условию (7.27) не удовлетворяет.
недостижима (так как нельзя взять полином R(p)равным нулю, а других возможностей для указанной цели нет). Абсолютная инвариантность к измеряемому возмущению f1 достижима (так как есть возможность выбора полинома P1(p)), а по отношению к задающему воздействию g – недостижима, так как заданный объект условию (7.27) не удовлетворяет. -изображения и, кроме того, если возмущения и задающее воздействие не имеют одинаковых спектральных составляющих.
-изображения и, кроме того, если возмущения и задающее воздействие не имеют одинаковых спектральных составляющих. с, перерегулирование не более 5% .
с, перерегулирование не более 5% . . Так как в уравнении (7.39) воздействие f2 умножается на полином
. Так как в уравнении (7.39) воздействие f2 умножается на полином  . (7.40)
. (7.40) – некоторый полином меньшей степени, чем степень полинома R(p).
– некоторый полином меньшей степени, чем степень полинома R(p). . Отсюда следует, что корень
. Отсюда следует, что корень  множителя
множителя  должен быть корнем полинома
должен быть корнем полинома  , (7.41)
, (7.41) – некоторый новый полином. Тогда условие абсолютной инвариантности системы к воздействию f1 принимает вид
– некоторый новый полином. Тогда условие абсолютной инвариантности системы к воздействию f1 принимает вид ,
, . (7.42)
. (7.42) , где
, где  – произвольный полином.
– произвольный полином.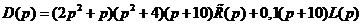 (7.43)
(7.43) , (7.44)
, (7.44) – некоторый полином.
– некоторый полином. удовлетворяет условию (7.44). Подставив правую часть (7.44) в равенство (7.43), сократим общий множитель (p + 10) в обеих частях этого равенства. В результате получим полиномиальное уравнение
удовлетворяет условию (7.44). Подставив правую часть (7.44) в равенство (7.43), сократим общий множитель (p + 10) в обеих частях этого равенства. В результате получим полиномиальное уравнение , (7.45)
, (7.45) .
. , необходимо, прежде всего, выбрать его степень. Она определяется из условия разрешимости полиномиального уравнения (7.45) следующим образом. Если перемножить полиномы в левой части этого уравнения и приравнять коэффициенты при одинаковых степенях в левой и правой его части друг к другу, то получится система линейных алгебраических уравнений относительно коэффициентов неизвестных полиномов
, необходимо, прежде всего, выбрать его степень. Она определяется из условия разрешимости полиномиального уравнения (7.45) следующим образом. Если перемножить полиномы в левой части этого уравнения и приравнять коэффициенты при одинаковых степенях в левой и правой его части друг к другу, то получится система линейных алгебраических уравнений относительно коэффициентов неизвестных полиномов  , (7.46)
, (7.46) . (7.47)
. (7.47)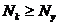 можно выбрать степени полиномов
можно выбрать степени полиномов  , то, согласно (7.41),
, то, согласно (7.41),  . Примем, что
. Примем, что  , тогда по (7.45)
, тогда по (7.45)  . Подставив эти выражения в (7.46), (7.47) и в неравенство
. Подставив эти выражения в (7.46), (7.47) и в неравенство  . Отсюда находим минимальное значение r = 3. При этом степени полиномов:
. Отсюда находим минимальное значение r = 3. При этом степени полиномов:  ,
,  ,
,  . Таким образом, в соответствии с найденными значениями степеней можно записать общие выражения для искомых полиномов
. Таким образом, в соответствии с найденными значениями степеней можно записать общие выражения для искомых полиномов  ,
,  .
. ,
, . (7.48)
. (7.48) ,
, 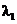 ,
,  ,
,  и
и 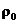 искомых полиномов
искомых полиномов  – коэффициенты желаемого характеристического полинома
– коэффициенты желаемого характеристического полинома  , которые определяются по условиям устойчивости и желаемого характера переходных процессов синтезируемой системы. Для определения коэффициентов этого полинома воспользуемся методом нормированных передаточных функций (см. § 6.4). В нашем случае степень знаменателя
, которые определяются по условиям устойчивости и желаемого характера переходных процессов синтезируемой системы. Для определения коэффициентов этого полинома воспользуемся методом нормированных передаточных функций (см. § 6.4). В нашем случае степень знаменателя  нормированной передаточной функции (6.13) равна степени
нормированной передаточной функции (6.13) равна степени  полинома
полинома  , порядок астатизма
, порядок астатизма  , а перерегулирование полагаем 5 %. По этим данным из табл. 6.1 выберем коэффициенты:
, а перерегулирование полагаем 5 %. По этим данным из табл. 6.1 выберем коэффициенты:  ,
,  ,
, 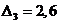 ,
,  и значение
и значение  . Так как заданное значение времени регулирования
. Так как заданное значение времени регулирования 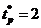 с, то по (6.14)
с, то по (6.14)  . Подставляя полученные значения в формулу (6.13), найдем
. Подставляя полученные значения в формулу (6.13), найдем .
. ;
;  ;
;  ,
, 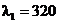 ,
,  , т.е.
, т.е.  ,
,  , а по (7.41) и (7.42) полиномы
, а по (7.41) и (7.42) полиномы  ,
,  .
. равен произведению
равен произведению 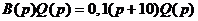 . Поэтому из условия
. Поэтому из условия  с учетом сокращённого двучлена
с учетом сокращённого двучлена  имеем уравнение
имеем уравнение  . Отсюда
. Отсюда  .
.
 . (7.49)
. (7.49) , представим это уравнение следующим образом:
, представим это уравнение следующим образом:
 .
.
 . (7.50)
. (7.50) является
является  , (7.51)
, (7.51) . (7.52)
. (7.52)
 и
и  соответственно.
соответственно. , (7.53)
, (7.53) , (7.54)
, (7.54) . (7.55)
. (7.55) и
и  . Так как оба блока имеют по одному выходу и по несколько входов, то для записи уравнений в переменных состояния целесообразно использовать соотношения для перехода от уравнений «вход-выход» к уравнениям в переменных состояния, соответствующие канонической наблюдаемой форме (см. § 3.8). Обозначив через
. Так как оба блока имеют по одному выходу и по несколько входов, то для записи уравнений в переменных состояния целесообразно использовать соотношения для перехода от уравнений «вход-выход» к уравнениям в переменных состояния, соответствующие канонической наблюдаемой форме (см. § 3.8). Обозначив через  и
и  переменные состояния этих блоков, получим
переменные состояния этих блоков, получим ,
, ,
, ,
,  ,
,  .
. , являются спектральной моделью внешнего гармонического воздействия с частотой
, являются спектральной моделью внешнего гармонического воздействия с частотой  . Нетрудно убедиться, что передаточная функция
. Нетрудно убедиться, что передаточная функция  синтезированной системы имеет в качестве множителя полином
синтезированной системы имеет в качестве множителя полином  , который не исчезает при малых вариациях всех коэффициентов системы, кроме коэффициента обратной связи равного 4 (рис. 7.8).
, который не исчезает при малых вариациях всех коэффициентов системы, кроме коэффициента обратной связи равного 4 (рис. 7.8).