
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Признаки подобия треугольников.1) Признак подобия треугольников по двум углам: - если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Признак подобия треугольников по двум сторонам и углу между ними: - если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны. 3) Признак подобия треугольников по трем сторонам: - если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Подобие прямоугольных треугольников. Если один из острых углов прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу
Средняя линия
Свойство средней линии треугольника Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Пропорциональные отрезки в прямоугольном треугольнике Определение: отрезок х называется средним пропорциональным или средним геометрическим между двумя отрезками а и в, если а : х = х : в. Пропорциональные отрезки в треугольнике Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:
12. Соотношение между сторонами и углами прямоугольного треугольника. Решение прямоугольных треугольников 
В прямоугольном треугольнике катет, противоположный одного из острых углов, равна произведению гипотенузы на синус этого угла.
В прямоугольном треугольнике катет, противоположный одного из острых углов, равна произведению прилегающего катета на тангенс этого угла.
В прямоугольном треугольнике катет, прилегающий к одному из острых углов, равна произведению гипотенузы на косинус этого угла.
В прямоугольном треугольнике катет, прилегающий к одному из острых углов, равна произведению противоположного катета на единицу, разделенную на тангенс этого угла.
Гипотенузы прямоугольного треугольника равен отношению противоположного одного из острых углов катета к синуса этого угла.
Гипотенузы прямоугольного треугольника равен отношению прилегающего к одному из острых углов катета к косинуса этого угла.
13.Окружность — геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центра окружности Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведенному в эту точку, называется касательной Свойства касательной 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. 2. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. 14. Центральный угол — это угол, вершина которого находится в центре окружности. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°. Центральный угол равен градусной мере дуги, на которую опирается. Вписанные углы, опирающиеся на одну и ту же дугу, равны. Вписанный угол, опирающийся на диаметр, - прямой. 15. Четыре замечательные точки в треугольнике: 1) три медианы пересекаются в одной точке, являющейсяцентром тяжести треугольника; 2) три биссектрисы пересекаются в одной точке (центре вписанной окружности); 3) три высоты (или их продолжения) пересекаются в одной точке («ортоцентре»); 4) три серединных перпендикуляра пересекаются в одной точке (центре описанной окружности). 16.Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Свойства[править | править исходный текст] · Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности). · Около любого правильного многоугольника(все углы равны) можно описать окружность, и притом только одну. Для треугольника[править | править исходный текст]
· Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечениясерединных перпендикуляров .· У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, упрямоугольного — на середине гипотенузы. Для четырехугольника[править | править исходный текст]
Вписанный простой (без самопересечений) четырёхугольник необходимо является выпуклым. Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180° ( Можно описать окружность около: · любого прямоугольника (частный случай квадрат) · любой равнобедренной трапеции · любого четырехугольника, у которого сумма противоположных углов равна 180 градусов У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон:[1] |AC|·|BD| = |AB|·|CD| + |BC|·|AD| Площадь четырёхугольника, вписанного в окружность, можно вычислить по формуле Брахмагупты:
17. Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех его сторон. Свойства вписанной окружности: · В каждый треугольник можно вписать окружность, притом только одну. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 409. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
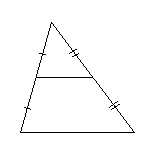 Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

 радиан).
радиан).