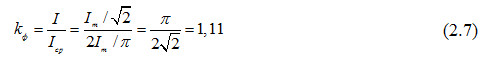Аналитический метод с использованием комплексных чисел

Синусоидальный ток i(t) = Imsin(ωt + ψ) можно представить комплексным числом Ím на комплексной плоскости Ím = Im^ejψ,

где амплитуда тока Im – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока.

Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.

Билет 6

Действующее и среднее значения синусоидального тока

О величине синусоидального тока принято судить не по мгновенному или амплитудному значениям, а по его действующему значению, которое еще называют среднеквадратичным или эффективным значением.

Действующее значение тока:

Аналогично U=U_m/√2; E=E_m/√2.

Под действующим значением синусоидального тока понимают такой ток, который за время, равное периоду, выделяет такое же количество тепла, что и эквивалентный ему постоянный ток.

Отношение амплитудного значения синусоидально изменяющейся функции к ее действующему значению называют коэффициентом амплитуды k_a.

Для синусоидального тока:

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за половину периода:

Отношение действующего значения периодически изменяющейся функции к ее среднему значению называют коэффициентом формы k_ф. Для синусоидального тока коэффициент формы:

Билет 7