
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Симметричные составляющие трехфазной системы векторовРассмотрим, что представляют собой системы прямой, обратной и нулевой последовательностей фаз и каковы возможности определения их по заданной несимметричной трехфазной системе векторов. Ввиду того, что фазные ЭДС, напряжения и токи в симметричных системах смещены друг относительно друга по фазе на 120°, для краткости математической записи, как правило, используют оператор
a4 = a Три единичных вектора При помощи оператора
Понятно, что Умножение вектора на Таким образом, с помощью введённого оператора «а» легко выразить каждую из симметричных составляющих прямой, обратной и нулевой последовательностей. Симметричная система прямой последовательности(прямого чередования фаз A, B, C) состоит из трех векторов
Рис. 57. Используя оператор «
Симметричная система обратной последовательности(обратного чередования фаз) состоит из трех векторов
 Система нулевой последовательности
Используя принцип наложения, любую исходную несимметричную систему трех векторов
С учетом (4.1, 4.2, 4.3) получаем:
Полученная система уравнений позволяет аналитически путём сложения определить векторы Однако, при этом легко решается и обратная задача, а именно – определение симметричных составляющих (
Поскольку Для определения составляющей прямой последовательностивторое уравнение в системе (4.4) необходимо умножить на «
Учитывая, что Для получения составляющих обратной последовательности второе уравнение в (4.4) следует умножить на a2, а третье – на а и тоже сложить. В результате получим
Понятно при этом, что Таким образом, полученные для Определение симметричных составляющих можно выполнить аналитически по комплексным изображениям исходных векторов Для трехфазных цепей в отношении системы нулевой последовательности можно сделать три важных вывода. 1. Совпадающие между собою по величине и фазе составляющие нулевой последовательности в линейных напряжениях трехфазных цепей отсутствуют. В случае, если фазы генератора соединены по схеме «звезда» и в них присутствуют нулевые последовательности, в каждом из линейных напряжений их нет, т.к.
При соединении фаз генератора по схеме «треугольник»
Понятно, что при 3 Это значит, что нулевая составляющая в каждой фазе ЭДС полностью уравновешивает (компенсируется) падением напряжения внутри фазы. 2. В трехфазной трехпроводной цепи векторная сумма линейных токов в соответствии с первым законом Кирхгофа равна нулю. Поэтому составляющие нулевой последовательности в линейных токах таких цепей равны нулю:
3. В трехфазной цепи с нейтральным проводом ток в нейтральном проводе равен утроенному значению составляющей нулевой последовательности:
Иллюстрация действий при графическом способе определения векторов прямого, обратного и нулевого чередования фаз по исходной (известной) несимметричной системе векторов Составляющая Для определения напряжений прямой и обратной последовательностей нужно сложить векторы по формулам:
При построении векторов необходимо учитывать, что умножение вектора на Из диаграмм находим:
Рис. 58. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 290. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . При этом
. При этом ,
, и
и .
. – образуют симметричную систему, следовательно,
– образуют симметричную систему, следовательно,  .
.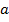 обычная симметричная система трехфазных ЭДС может быть представлена в следующем виде:
обычная симметричная система трехфазных ЭДС может быть представлена в следующем виде: ;
; .
. соответствует повороту этого вектора против часовой стрелки на 120°, а умножение на
соответствует повороту этого вектора против часовой стрелки на 120°, а умножение на  – такому же повороту на 240°.
– такому же повороту на 240°. , равных по модулю, сдвинутых относительно друг друга на 120° и имеющих порядок следования (по часовой стрелке)
, равных по модулю, сдвинутых относительно друг друга на 120° и имеющих порядок следования (по часовой стрелке)  -
- 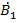 -
-  (рис. 57а).
(рис. 57а).
 через вектор
через вектор  записываются следующим образом:
записываются следующим образом: (4.1)
(4.1) , равных по модулю, смещенных относительно друг друга на 120° и имеющих порядок следования
, равных по модулю, смещенных относительно друг друга на 120° и имеющих порядок следования  -
-  -
-  (рис. 57в). При этом фазы B и C здесь меняются местами.
(рис. 57в). При этом фазы B и C здесь меняются местами. (4.2)
(4.2) образуется тремя равными векторами, совпадающими между собой по фазе (рис. 57с).
образуется тремя равными векторами, совпадающими между собой по фазе (рис. 57с). (4.3)
(4.3) легко представить в виде суммы трех симметричных составляющих:
легко представить в виде суммы трех симметричных составляющих: ;
; ;
; .
. ;
; . (4.4)
. (4.4) , если они известны.
, если они известны. ,
,  ,
,  ,
,  ), которыми может быть представлена любая несимметричная система векторов
), которыми может быть представлена любая несимметричная система векторов  ,
,  ,
,  . Для того чтобы найти нулевую последовательность
. Для того чтобы найти нулевую последовательность  , достаточно сложить три уравнения (4.4):
, достаточно сложить три уравнения (4.4):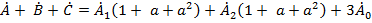 .
. . Понятно, что
. Понятно, что 

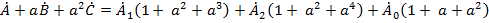
 ,
,  , получим:
, получим:  . Притом
. Притом 
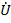 AB0 =
AB0 = 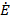 AB0 +
AB0 + 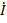 AB0zвн +
AB0zвн +  , ибо
, ибо  , т.к. сумма симметричных составляющих токов прямой и обратной последовательности в нейтральном проводе равна нулю.
, т.к. сумма симметричных составляющих токов прямой и обратной последовательности в нейтральном проводе равна нулю. , тогда
, тогда  – масштаб напряжений.
– масштаб напряжений. .
. .
.