
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальные уравнения первого порядка
Задача 4.Найти общее решение уравнения Решение:
Данное уравнение является однородным, так как коэффициенты при Если Сократив на
Мы получили уравнение с разделенными переменными относительно
Потенцируя, находим Задача 5.Найти общее решение уравнения Решение:
Данное уравнение является линейным, так как оно содержит искомую функцию Применяем подстановку
или Так как искомая функция При таком выборе функции Уравнение (2) есть уравнение с разделяющимися переменными относительно
Чтобы равенство (2) имело место, достаточно найти одно какое – либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С=0. Подставив в (3) найденное выражение для |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 199. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
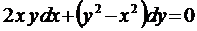 .
. и
и  есть однородные функции одного и того же измерения (второго) относительно переменных
есть однородные функции одного и того же измерения (второго) относительно переменных  . Применяем подстановку
. Применяем подстановку  , где
, где  – некоторая функция аргумента
– некоторая функция аргумента  .
. , то дифференциал
, то дифференциал 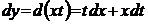 , и данное уравнение примет вид
, и данное уравнение примет вид 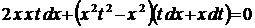 .
. , будем иметь:
, будем иметь: ;
; ;
;
 ;
; ;
; .
. и
и  . Интегрируя, находим общее решение этого уравнения:
. Интегрируя, находим общее решение этого уравнения: ;
;  ;
; ;
;  .
. , или
, или  . Из введенной подстановки следует, что
. Из введенной подстановки следует, что  . Следовательно,
. Следовательно, 
 – общее решение данного уравнения.
– общее решение данного уравнения. .
. и её производную
и её производную  в первой степени и не содержит их произведений.
в первой степени и не содержит их произведений. , где
, где  и
и  – некоторые неизвестные функции аргумента
– некоторые неизвестные функции аргумента  . Если
. Если  и данное уравнение примет вид
и данное уравнение примет вид ,
, . (1)
. (1) (2)
(2) . (3)
. (3) ;
; 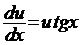 ;
;  ;
; ;
;  ,
,  .
. , получим:
, получим:  ;
;  ;
;  ;
;  . Интегрируя, получаем
. Интегрируя, получаем 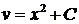 . Тогда
. Тогда  – общее решение данного уравнения.
– общее решение данного уравнения.