
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнение прямой в отрезкахЕсли в общем уравнении прямой (5) С¹0, то разделив все его члены на С, получим уравнение вида
где а =–С/А, b=–С/В. Его называют уравнением прямой в отрезках. В нем а является абсциссой точки пересечения прямой с осью Ох, а b – ординатой точки пересечения прямой с осью Оу. Поэтому а и b называют отрезками прямой на осях координат.
Уравнение прямой, проходящей через две заданные точки М1(x1;y1) и М2(x2;y2)
Пример 1. Составить уравнение прямой, отсекающей на оси ординат отрезок b=–2 и имеющей угловой коэффициент k=3. Решение: Применяя формулу (6), запишем уравнение искомой прямой: у=3х–2. Ответ: у=3х–2. Пример 2. Составить уравнение прямой, отсекающей на осях координат отрезки а=2,5 и b=1,5. Решение: Воспользовавшись формулой (8) имеем: х/2,5+у/1,5=1. Приведем это уравнение к общему виду: (2/5)х+(2/3)у=1 или 6х+10у–15=0. Ответ: 6х+10у–15=0. Пример 3. Дано общее уравнение прямой 2х–5у+10=0. Написать: 1) уравнение с угловым коэффициентом; 2) уравнение в отрезках; 3) построить прямую. Решение: 1) Разрешив уравнение относительно у, получим уравнение с угловым коэффициентом: 5у=2х+10 или у=(2/5)х+2. Здесь k=2/5; b=2. 2) Перенесем свободный член уравнения в правую часть и разделим обе части на (–10): 2х/(–10)–5у/(–10)=1. Здесь а=–5; b=2. 3) Построим прямую:
Пример 4. Составить уравнение прямой, проходящей через начало координат и точку М(–1;5). Решение: Воспользуемся формулой (9)
–y=5x; 5x+y=0 – общее уравнение прямой. Ответ: Пример 5. Составить уравнение прямой, проходящей через точки А(2;–3) и Решение: Применяя формулу (9) и подставляя х1=2, у1=–3, х2=–4, у2=5, получим: (у–(–3))/(5–(–3))=(х–2)/(–4–2) или (у+3)/8=(х–2)/(–6), 4(х–2)=–3(у+3).  Искомое уравнение имеет вид 4х+3у+1=0. Ответ: 4х+3у+1=0 Пример 6. Даны вершины треугольника А(–1; 1), В(5; 7), С(–9; 3). Найти уравнения медиан АD, BE, CN. Решение: Найдем сначала координаты точки D – середины стороны ВС по формуле (4): х=(5–9)/2=–2; у=(7+3)/2=5, т. е. D(–2; 5). Уравнение медианы AD находится с помощью уравнения прямой, проходящей через две точки: (у–1)/(5–1)=(х+1)/(–2+1) или (у–1)/4=(х+1)/(–1), т. е. 4х+у+3=0. Ответ: Уравнение медианы AD: 4х+у+3=0. Уравнения медиан ВЕ и CN находятся аналогично.
Угол между двумя прямыми Угол между прямыми y1=k1x+b1 и y2=k2x+b2 определяется по формуле
Условие параллельности прямых Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты, т.е. k2=k1. Условие перпендикулярности прямых
Две прямые перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно –1, т.е. k2=–1/k1. Пример 7. Определить острый угол между прямыми у1=3х +1 и у2=–2х–5. Решение: Полагая k1=3 и k2=–2 и применяя формулу (10), получим: tgj =(–2–3)/(1+(–2)×3)=–5/(–5)=1, т.е. j =p/4=0,785 рад. Ответ: j =0,785 рад. Пример 8. Показать, что прямые 7х+3у–5=0 и 14х+6у+1=0 параллельны. Решение: Приведя уравнение каждой прямой к виду с угловым коэффициентом, получаем: у=(–7/3)х+5/3 и у=(–7/3)х+1/14. Ответ: Угловые коэффициенты этих прямых равны: k1=k2=–7/3, т. е. прямые параллельны. Пример 9. Показать, что прямые 2х–3у+7=0 и 6х+4у–3=0 перпендикулярны. Решение: После приведений уравнений к виду с угловым коэффициентом получаем: у=(2/3)х+7/3 и у=(–3/2)х+3/4. Здесь k1=2/3, k2=–2/3. Ответ: Так как k==–1/k1, то прямые перпендикулярны. Пример 10. Даны вершины треугольника А(–5;0), В(–3;–2), С(–7;6). Найти уравнение высоты AD. Решение: Составим уравнение прямой ВС по двум точкам и определим её угловой коэффициент kВС=–2. В силу перпендикулярности прямых AD и BC kAD=–1/kВС, т. е. kAD=–1/2. Уравнение высоты, проведенной из вершины А будет иметь вид: у–0=(х+5)/2 или х–2у+5=0. Ответ: х–2у+5=0.
КРИВЫЕ ВТОРОГО ПОРЯДКА Кривой второго порядка называется множество точек М(x;y) на плоскости Оху, координаты которых удовлетворяют следующему общему уравнению кривой второго порядка:
где а11, а22, а0 - заданные числа. Далее рассмотрим наиболее простые частные случаи этого уравнения. Окружность Окружность – это множество точек плоскости, равноудаленных от одной точки (центра). Если С(а;b) – центр окружности, а R – радиус окружности, то уравнение окружности имеет вид:
В частности, если центр окружности совпадает с началом координат, то уравнение (12) примет вид:
Общее уравнение окружности имеет вид:
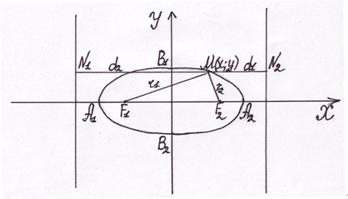
Полезно помнить, что общее уравнение окружности содержит старшие члены х2 и у2 с равными коэффициентами и отсутствует член с произведением х на у. Пример 1. Определить координаты центра и радиус окружности 2х2 +2у2–8х+6у+12=0. Решение: Разделив уравнение на 2 и сгруппировав члены уравнения, получим: х2–4х+у2+3у=–6. Дополним выражения х2–4х и у2+3у до полных квадратов, прибавив к первому двучлену 4, а ко второму (3/2)2, одновременно к правой части прибавляется сумма этих чисел: (х2–4х+4)+(у2+3у+(3/2)2)=–6+4+9/4 или (х–2)2+(у+3/2)2=1/4. Таким образом, координаты центра окружности а=2, b=–3/2, а радиус окружности R=1/2. Ответ: Центр О(2;–3/2), R=1/2. Эллипс Эллипсом называют множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная больше расстояния между фокусами. Если оси координат расположены по отношению к эллипсу так, как на рис.1, а фокусы эллипса находятся на оси Ох на равных расстояниях от начала координат в точках F1(C;0) и F2(–С;0), то каноническое уравнение эллипса имеет вид:
Рис.1 Здесь а – большая полуось, b – малая полуось эллипса. Причем, а, b, и с (с – половина расстояния между фокусами) связаны соотношением
Форма эллипса (мера его сжатия) характеризуется эксцентриситетом е=с/а (так как с<а, то е<1). Расстояние до некоторой точки М эллипса от его фокусов называется фокальными радиусами-векторами этой точки. Их обычно обозначают r1 и r2 (в силу определения эллипса для любой его точки r1+r2=2а). В частном случае, когда а=b (с=0, е=0), фокусы сливаются в одной точке – центре; эллипс превращается в окружность с уравнением х2+у2=а2. Пример 2. Написать каноническое уравнение эллипса, если даны его полуоси а=5 и b=4. Решение: Подставляя в уравнение (15) а2=25, b2=16, получим каноническое уравнение эллипса х2/25+у2/16=1. Ответ: х2/25+у2/16=1. Пример 3. Написать уравнение эллипса, если расстояние между фокусами равно 6, а большая полуось равна 5. Решение: Зная, что а=5 и 2с=6, найдем малую полуось эллипса из соотношения b2=a2–c, т. е. b2=25–9=16. Уравнение эллипса: х2/25+у2/16=1. Ответ: х2/25+у2/16=1. Гипербола Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (2а), причем эта постоянная меньше расстояния между фокусами. Если поместить фокусы гиперболы в точках F1(c;0) и F2(–с;0), то каноническое уравнение гиперболы имеет вид:
где b2=с2–а2. Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а;0) и А2(–а;0) называются вершинами гиперболы. Отрезок |А1А2|=2а называется действительной осью гиперболы, а отрезок |В1В2|=2b – мнимой осью (рис.2). Гипербола имеет две асимптоты, уравнения которых имеют вид:
Прямая называется асимптотой гиперболы, если расстояние точки М(х;у) гиперболы от этой прямой стремится к нулю при х®¥ или х®–¥. Отношение
называются эксцентриситетом гиперболы.
Рис. 2 Пример 4. Написать каноническое уравнение гиперболы, фокусы которой лежат на оси Ох, если а=4, с=5. Решение: Найдем мнимую полуось гиперболы из соотношения b2=с2–а2, b2=25–16=9. Имея а2=16, b2=9, запишем уравнение гиперболы х2/16–у2/9=1.
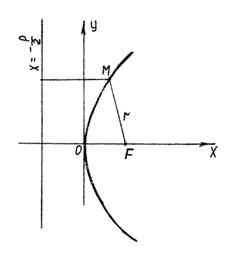
Парабола Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы является прямая х=–р/2, а фокусом – точка F(р/2;0), то уравнение параболы имеет вид:
Эта парабола расположена симметрично относительно оси абсцисс (рис. 3), р>0.
Рис. 3 Уравнение
является уравнением параболы, симметричной относительно оси ординат. При р>0, параболы (20) и (21) обращены в положительную сторону соответствующей оси, а при р<0 – в отрицательную сторону. Пример 5. Написать каноническое уравнение параболы, если расстояние фокуса от директрисы равно 10. Решение: Расстояние фокуса от директрисы р=10. Подставив в уравнение параболы у2=2рх значение р=10, получим у2=20х. Ответ: у2=20х. Пример 6. Найти уравнение директрисы и координаты фокуса параболы у2=4х. Решение: Данная парабола симметрична относительно оси Ох и расположена справа от оси Оу. Из уравнения (20) находим 2р=4, откуда р=2. Директрисой служит прямая, параллельная оси Оу и отстоящая от последней на расстоянии р/2=1. Следовательно, уравнение директрисы параболы будет х=–1. Расстояние фокуса от начала координат равно р/2, поэтому абсцисса фокуса будет х=1. Итак, фокус находится в точке F(1;0). Ответ: уравнение директрисы х=–1, фокус F(1;0).
КОНТРОЛЬНЫЕ ЗАДАНИЯ Вопросы для самопроверки 1. Напишите уравнение прямой с угловым коэффициентом. 2. Напишите общее уравнение прямой. 3. Напишите уравнение прямой, проходящей через данную точку в данном направлении. 4. Напишите уравнение прямой, проходящей через две точки. 5. Напишите уравнение прямой в отрезках. 6. Напишите формулу нахождения угла между прямыми. 7. Напишите общее уравнение линии второго порядка. 8. Напишите каноническое уравнение окружности. 9. Напишите каноническое уравнение эллипса. 10. Что называется фокусом эллипса? Напишите формулу нахождения координат фокуса эллипса. 11. Что называется эксцентриситетом эллипса? Напишите формулу нахождения эксцентриситета эллипса. 12. Какие прямые называются директрисами эллипса? 13. Напишите каноническое уравнение гиперболы. 14. Что называется фокусом гиперболы? Напишите формулу нахождения координат фокуса гиперболы. 15. Что называется эксцентриситетом гиперболы? Напишите формулу нахождения эксцентриситета гиперболы. 16. Какая ось гиперболы мнимая? действительная? 17. Что называется основным прямоугольником гиперболы? 18. Напишите каноническое уравнение параболы? 19. Что называется параметром параболы? 20. Что является осью симметрии параболы? 21. Что называется фокусом параболы? Напишите формулу нахождения координат фокуса параболы. Задания для самопроверки 1. Составить уравнение окружности: а) центр окружности совпадает с началом координат и ее радиус R=3; б) центр окружности совпадает с точкой С(2;-3) и ее радиус R=7; в) окружность проходит через начало координат и ее центр совпадает с точкой С(6;-8); г) окружность проходит через точку А(2;6) и ее центр совпадает с точкой С(-1;2); д) точки А(3;2) и В(–1;6) являются концами одного из диаметров окружности. 2. Написать уравнения окружностей радиуса 3. Установить, как расположена точка А(1;–2) относительно каждой из следующих окружностей – внутри, вне или на контуре: а) б) в) г) д) 4. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, что: а) его полуоси равны 5 и 2; б) его большая ось равна 10, а расстояние между фокусами 2c=8; в) его малая ось равна 24, а расстояние между фокусами 2c=10; г) расстояние между его фокусами 2c=6 и эксцентриситет e=3/5; д) его большая ось равна 20, а эксцентриситет e=3/5. 5. Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично начала координат, зная, что: а) его полуоси равны соответственно 7 и 2; б) его большая ось равна 10, а расстояние между фокусами 2c=8; в) расстояние между его фокусами 2c=24 и эксцентриситет e=12/13; г) его малая ось равна 16, а эксцентриситет e=3/5. 6. На эллипсе 7. Определить, какие из точек A1(-2;3), A2(2;–2), A3(2;–4), A4(–1;3), 8. Составить уравнения эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если даны: а) точка М1( б) точка М1(2;–2) эллипса и его большая полуось a=4; в) точки М1(4; г) точка М1( д) точка М1(2;–-5/3) эллипса и его эксцентриситет e=2/3. 9. Составить уравнение эллипса, зная, что: а) его большая ось равна 26, фокусы F1(–10; 0), F2(14;0); б) его малая ось равна 2, фокусы F1(–1;–1), F2(1; ); в) его фокусы F1(–2; /3), F2(2;–3/2) и эксцентриситет e= 10. Составить уравнение эллипса, если известны его эксцентриситет 11. Составить уравнение эллипса, если известны его эксцентриситет e=1/2, фокус F(–4;1) и уравнение соответствующей директрисы 12. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что: а) ее оси 2a=10 и 2b=8; б) расстояние между фокусами 2c=10 и ось 2b=8; в) расстояние между фокусами 2c=6 и эксцентриситет e=3/2; г) ось 2a=16 и эксцентриситет e=5/4. 13. Составить уравнение гиперболы, фокусы которого расположены на оси ординат симметрично относительно начала координат, зная, что: а) ее полуоси a=6, b=18 (буквой а обозначена полуось гиперболы, расположенная на оси абсцисс); б) расстояние между фокусами 2с=10 и эксцентриситет e=5/3. 14. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны: а) очки M1(6;–1), M2(–8; б) точка М1(–5;3) гиперболы и эксцентриситет e= в) точка М1(9/2;–1) гиперболы с уравнения асимптот 15. Составить уравнение параболы, вершина которой находится в начале координат, зная, что: а) парабола расположена в правой полуплоскости, симметрично относительно оси Ох и ее параметр р=3; б) парабола расположена в левой полуплоскости симметрично относительно оси Ох и ее параметр р=0,5; в) парабола расположена в верхней полуплоскости симметрично относительно оси Оу и ее параметр р=1/4; г) парабола расположена в нижней полуплоскости симметрично оси Оу и ее параметр р=3. 16. Составить уравнение параболы, вершина которой находится в начале координат, зная, что: а) парабола расположена симметрично относительно оси Ох и проходит через точку А(9;6); б) парабола расположена симметрично относительно оси Ох и проходит через точку В(–1;3); в) парабола расположена симметрично относительно оси Оу и проходит через точку С(1;1); г). парабола расположена симметрично относительно оси Оу и проходит через точку D(4;–8). 17. Найти фокус F и уравнение директрисы параболы у2=24х. 18. Вычислить фокальный радиус точки М параболы у2=20х, если абсцисса точки М равна 7. 19.Вычислить фокальный радиус точки М параболы у2=12х, если ордината точки М равна 6. 20.На параболе у2=16х найти точки, фокальный радиус которых равен 13. 21.Установить, что каждое из следующих уравнений определяет параболу, и найти ее вершины, величину параметра р и уравнение директрисы: а) у2=4х–8; б) у2=4–4х; в) х2=6у+2; г) х2=2–у. |
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 944. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 ;
;


 , касающихся прямой
, касающихся прямой  в точке М1(3;1).
в точке М1(3;1). ;
; ;
; ;
; 
 ;
; .
. найти точку, абсцисса которой равна –3.
найти точку, абсцисса которой равна –3. , какие внутри и какие вне его.
, какие внутри и какие вне его.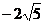 ;2) эллипса и его малая полуось b=3;
;2) эллипса и его малая полуось b=3; ) и М2(
) и М2(  ;3) эллипса;
;3) эллипса; ;–1) эллипса и его эксцентриситет e=2/3;
;–1) эллипса и его эксцентриситет e=2/3; .
.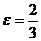 , фокус F(–4; 1) и уравнение соответствующей директрисы
, фокус F(–4; 1) и уравнение соответствующей директрисы  .
. .
. ;
; .
.