
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Векторное произведение, смешанное произведение.Стр 1 из 4Следующая ⇒ Декартова система координат. Векторы. Скалярное произведение. Деление отрезка в заданном отношении.
Если в пространстве задана прямоугольная декартова система координат Oxyz, то точка М пространства, имеющая координаты x (абcцисса), y (ордината) и z (аппликата), обозначается M(x,y,z). Расстояние между двумя точками Вектором называется направленный отрезок. Векторы можно складывать (по правилу треугольника (Рис. 1a) или правилу параллелограмма (Рис. 1б)), вычитать (Рис. 1с), умножать на число (Рис 1д, 1е).
Чтобы вычислить координаты вектора, необходимо от координат конца вектора отнять координаты начала вектора Проекция вектора Скалярное произведение используется для вычисления длин отрезков и углов между векторами. Скалярное произведение вычисляется по формуле Свойства скалярного произведения 1. 2. для не нулевых векторов 3. 4. 5. Задача 1. В треугольнике АВС точка М делит сторону АС в отношении m:n. Вычислите Решение.
Обозначим:
тогда
Теорема о делении отрезка в заданном отношении
1.1 Координаты вершин треугольника A(1, 2, 3), В(0, 1, -1), С(-2,0,0). Найдите: 1. координаты вектора 2. координаты центра тяжести треугольника АВС, 3. координаты точек M и N, делящих отрезок 4. длину вектора 5. проекцию вектора  6. координаты вершины D, параллелограмма ABCD, 7. длину диагонали BD, параллелограмма ABCD, 8. на оси OX точку, равноудалённую от вершин AB. 9. Будет ли угол A в треугольнике 10. Докажите равенство
Векторное произведение, смешанное произведение.
Векторное произведение используется для вычисления площадей треугольников и других фигур. Векторным произведением вектора 1. модуль вектора 2. 3. тройка векторов Свойства векторного произведения: 1. 2. 3. 4. Координаты векторного произведения вычисляются по формуле.
2.1 Координаты точек а. вычислите площадь треугольника ABC, б. вычислите с. вычислите площадь параллелограмма ABCD , д. координаты векторов, перпендикулярных плоскости ABC , е. значение параметров
Смешанное произведение используется для вычисления объёмов. Смешанное произведение векторов Смешанное произведение вычисляется по формуле
Свойства смешанного произведения:
Смешанное произведение равно нулю, если один из перемножаемых векторов равен нулю, либо два из перемножаемых векторов параллельны, либо три перемножаемых вектора компланарны (т. е. лежат в одной плоскости). При перестановке любых двух векторов смешанное произведение меняет знак. Объём тетраэдра, построенного на векторах 2.2 Координаты точек a. oбъём тетраедра ABCD, б. объём тетраэдра BMND, с. площадь треугольника 2.3 Координаты векторов а. векторы б. ориентация тройки векторов с.
Прямая в пространстве: параметрическое уравнение прямой, каноническое уравнение прямой. Взаимное расположение двух прямых: угол между прямыми, условие параллельности и перпендикулярности прямых.
Прямая в пространстве определяется точкой
Каждое значение параметра t задёт координаты точки прямой. Исключив параметр
Углом между двумя прямыми называется острый положительный угол между двумя векторами, параллельными этим прямым. Углом между прямой и плоскостью называется острый положительный угол между вектором, параллельным прямой, и вектором, лежащим на проекции данной прямой на плоскость. 3.1 Найдите угол между прямыми
3.2 При каких значениях параметров
3.3 При каком значении параметра
3.4 Напишите уравнение прямой, проходящей через точку 3.5 Напишите уравнение прямой, проходящей через точку 3.6 Напишите уравнение прямой, проходящей через точки (2,-1,5) и (1,1,4). |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 190. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  вычисляется по формуле
вычисляется по формуле  .
.

 на вектор
на вектор  вычисляется по правилу
вычисляется по правилу  .
. . Если
. Если  и
и  , то
, то  . Длина вектора вычисляется по формуле
. Длина вектора вычисляется по формуле 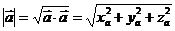 . Косинус угла между векторами вычисляется по формуле
. Косинус угла между векторами вычисляется по формуле  .
. ,
, ,
, ,
, ,
, .
. и угол
и угол  .
.
 ,
, ,
, ,
,  ,
,  ,
, ,
, .
.
 ,
,  ,
, .
. ,
, на три равные части,
на три равные части, ,
, ,
, острым?
острым? .
. , определяемый следующим образом:
, определяемый следующим образом: равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  ),
),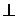

 ,
, , если
, если  , либо
, либо  , либо
, либо  ,
, (сочетательное свойство),
(сочетательное свойство), (распределительное свойство).
(распределительное свойство). .
. ,
,  ,
,  . Используя векторное произведение
. Используя векторное произведение ,
,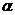 , при которых векторы
, при которых векторы  и
и  параллельны.
параллельны. и
и  .
. смешанное произведение может быть представлено с использованием скалярного и векторного произведений.
смешанное произведение может быть представлено с использованием скалярного и векторного произведений.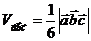 .
. . Точка М лежит на отрезке
. Точка М лежит на отрезке  , точка N лежит на отрезке
, точка N лежит на отрезке  , причём
, причём  и
и  . Используя теорему о делении отрезка в заданном отношении, вычислите:
. Используя теорему о делении отрезка в заданном отношении, вычислите: .
. ,
,  ,
,  . При каком значении параметра
. При каком значении параметра  лежат в одной плоскости (коллинеарны)
лежат в одной плоскости (коллинеарны) .
. , через которую проходит данная прямая, и вектором, параллельным данной прямой
, через которую проходит данная прямая, и вектором, параллельным данной прямой  . В параметрическом виде уравнение такой прямой имеет вид
. В параметрическом виде уравнение такой прямой имеет вид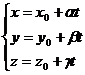 .
. , получим уравнение прямой в каноническом виде
, получим уравнение прямой в каноническом виде .
. и
и  .
. прямые
прямые будут параллельны?
будут параллельны? и
и  параллельно вектору
параллельно вектору  .
.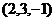 .
.