
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Наиболее сложные вопросы учебной программы ⇐ ПредыдущаяСтр 2 из 2 1. Построение математических моделей объектов промышленной электроэнергетики. 2. Построение решения задачи методом критериального программирования для класса задач с положительной степенью трудности. 3. Расчеты показателей надёжности систем с учётом преднамеренных отключений отдельных элементов. Задания самостоятельной работы Вариант задания выбирается в зависимости от двух последних цифр шифра студента. Например, шифр студента 200727, вариант задания – 7. Если предпоследняя цифра шифра нечетная, то вариант задания выбирается по последней цифре из второй десятки варианта (11, 12, …, 20). Например, шифр студента 200576, вариант – 16. Тема 1.Математические задачи и математическое моделирование в электроэнергетике Задача 1.1. Методом интерполяции определить уровень напряжения на шинах РУ 10(20) кВ., соответствующий минимуму потерь электрической энергии в распределительной сети. Исходные данные приведены в таблице 8.1. Задача 1.2.Найти аппроксимирующую функцию вида Исходные данные приведены в таблице 8.2 для различных марок кабелей и уровней напряжений. Тема 3.Критериальное программирование. Задача 3.1.Методом критериального анализа исследовать технико-экономическую модель линии электропередачи вида
где З - приведенные затраты на линию электропередачи, тыс.тенге/год;

Требуется: 1) найти экономически целесообразные значения оптимизируемых параметров ( 2) выявить технико-экономическую соразмерность затрат; 3) исследовать экономическую устойчивость уровня приведенных затрат при отклонении параметров от экономически целесообразных значений (построить график); 4) исследовать чувствительность экономических значений параметров и затрат к изменению исходных данных (построить график); 5) определить оптимальный вариант с учетом технических ограничений, накладываемых на Исходные данные по вариантам приведены в таблице 8.3, где
Обобщенные константы целевой функции определяются следующими выражениями:
где
где Тема 4.Применение теории вероятностей и математической статистики в электроэнергетических задачах Задача 4.1. Используя методы теории планирования эксперимента построить математическую модель оптимальных уровней напряжения линии электропередачи. В качестве влияющих факторов взять следующие переменные : X1 – передаваемая мощность (S); Х2 – время потерь электроэнергии (τ); Х3 – стоимость потерь электроэнергии (Сo). Диапазон варьирования факторов:
X1max=15MBA; X1min=2 MBA; Х2max=5500 ч; Х2min=1800 ч; Х3mах=1.5 тг/кВт×ч; Х3mix=0.3 тг/кВт×ч
Используя выражение для экономических значений уровней напряжений из задачи № 3.1 и задаваясь граничными значениями влияющих факторов, вычислить значение функции в каждом плановом опыте. Дисперсию воспроизводимости опытов можно принять как 5%-ое отклонение от среднего значения функции. Задача 4.2. Определить следующие статические показатели надежности восстанавливаемой системы электроснабжения: 1) вероятность отказа системы 2) интенсивность отказов системы 3) среднее время восстановления системы 4) среднее время безотказной работы системы Тс, если известны интенсивность отказов и время восстановления отдельных ее элементов, а также их параметры преднамеренных отключений. Исходные данные по вариантам приведены в таблице 8.4 и таблице 8.5.
Таблица 8.1 – Исходные данные для решения задачи № 1.1
Таблица 8.2 – Исходные данные для решения задачи № 1.2
Таблица 8.3 – Исходные данные для решения задачи № 3.1
Таблица 8.4 – Исходные данные для решения задачи № 4.1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 стоимостных показателей линии электропередачи в зависимости от сечения проводников. Определить точность аппроксимации.
стоимостных показателей линии электропередачи в зависимости от сечения проводников. Определить точность аппроксимации. ,
,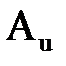 - обобщенная константа при параметре
- обобщенная константа при параметре  , тыс.тенге/кВα;
, тыс.тенге/кВα;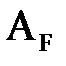 - обобщенная константа при параметре
- обобщенная константа при параметре  , тыс.тенге/мм2;
, тыс.тенге/мм2; - обобщенная константа, характеризующая потери электроэнергии в линии, тыс.тенге кВ2 мм2;
- обобщенная константа, характеризующая потери электроэнергии в линии, тыс.тенге кВ2 мм2; - коэффициент, характеризующий затраты на строительство одного километра линии от уровня напряжения, тыс.тенге/кВα км;
- коэффициент, характеризующий затраты на строительство одного километра линии от уровня напряжения, тыс.тенге/кВα км; - коэффициент, характеризующий затраты на строительство одного километра линии от сечения, тыс.тенге/мм2 км;
- коэффициент, характеризующий затраты на строительство одного километра линии от сечения, тыс.тенге/мм2 км; - показатель степени уровня напряжения;
- показатель степени уровня напряжения; - мощность, передаваемая по линии, МВ∙А;
- мощность, передаваемая по линии, МВ∙А; - протяженность линии, км;
- протяженность линии, км; - время потерь электроэнергии, тыс. час./год;
- время потерь электроэнергии, тыс. час./год; - удельные затраты на компенсацию потерь электроэнергии, тыс.тенге/кВт·ч.
- удельные затраты на компенсацию потерь электроэнергии, тыс.тенге/кВт·ч. ,
,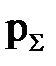 - суммарный нормативный коэффициент ежегодных отчислений (р∑ = 0,125 + 0,03 = 0,155).
- суммарный нормативный коэффициент ежегодных отчислений (р∑ = 0,125 + 0,03 = 0,155). ,
, 
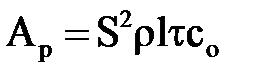 ,
, - удельное сопротивление проводника линии (для алюминия
- удельное сопротивление проводника линии (для алюминия  ).
). ;
; ;
; ;
; ,
кВ
,
кВ
 ,
кВ
,
кВ
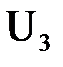 ,
кВ
,
кВ
 ,
кВ
,
кВ
 ,
кВт
,
кВт
 ,
кВт
,
кВт
 ,
кВт
,
кВт
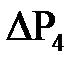 ,
кВт
,
кВт

 ,
,

 ,
,
 ,
час 103
,
час 103
 ,
,


