
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема о регулярности дополнения регулярного языка.Регулярность пересечения,разности и симметрической разности регулярных языков.Теор: Дополнение регулярного языка есть регулярный язык. Д-во: Пусть L-ря в алфавите v.Тогда дополнение языка L(как мн-ва слов) есть язык I=V*/L. Согласно торемы о детерминизации для L может быть построен детерминизированным КА М, допускаемый L.Поскольку в детерминизированном автомате из каждой вершины по каждому входному символу определен переход в точности в одну вершину, то какова бы не была цепочка х в алфавите V для нее найдется единственный путь в М,нач. в начальном состоянии,на которой читается цепочка Х. Ясно ,что цепочка Х допускается автоматом М, т.е. хÎL(M),Ûпоследнее состояние указанного пути явл. заключительным. ОтсюдаÞ,что цепочка хÏL(M)Ûкогда последнее состояние указанного пути не заключ. Но наш как раз и нужен КА М,который допускает исходный исходный КА МÞ превращая каждое заключительное состояние М в незаключетельное и наоборот, получим детерминизированный автомат,допускаемый дополнение языка L. Для " двух РЯ L1 иL2 справедливы следующие утверждения:1)Пересечение L1 ÇL2 регулярно 2)разность L1 /L2 регулярно 3)симм. разность L1 Док-во:1)L1 ÇL2=L1 ÈL2 2)L1 /L2 =L1 ÇL2 3) L1 Согласно определению(L КА М1 и М2 наз. эквивалентными если их языки совпадают),КА эквиваленты если допускаемые ими языки совпадают. Поэтому чтобы убедится в эквивалентности автоматов М1 и М2 достаточно доказать,что симметрическая разность языковL(M1) и L(M2) пуста. Для этого в свою очередь, достаточно построить автомат, допускающий эту разность и убедится в том, что допускаемый им язык пуст. В общем случае проблему распознавания того, что язык КА пуст, называют проблемой пустоты для КА. Чтобы решить эту проблему, достаточно найти множество заключенных состояний автомата,достижимых из нач. состояния.т.к. КА-это ориент. граф, то решить такую проблему можно с помощью поиска в ширину. Язык, допускаемый КА, пуст Û мн-во заключительных состояний, достижимых из исп. сост., пусто. Практически эквивалентность КА предпочтительнее распозновать, исп. алгоритм минимизации. 
10.1.Замкнутое полукольцо.Непрерывность операции сложения в замнкутом полукольце.Теорема о наименьшем решении линейного уравнения х=ах+b в замкнутом п/к. Замкнутое п/к-$=(S,+,.,0,1I): 1)оно идемпотентно 2)любая посл-ть эл-тов мн-ва S имеет т.в.г.относительно естественного порядка £ этого идемпотентного п/к. 3)операция «.» сохраняет т.в.г. последовательности " a sup sup Теорема:" конечное идемпотентное п/к замкнуто Док-во: поскольку носитель S идемп. п/к S=(S,+,.,0,1I) есть конечное множество,то множество эл-ов " последовательности в этом п/к конечно.Для нахождения точной верхней грани такой последовательности нужно найти точную верхнюю грань мн-ва р= идемпотентном п/к " последовательность имеет т.в.г. Условия хранения точных верхних граней имеют вид
a(p1+…pn)=ap1 +…+apn (p1+…+pn)*a=p1a+…+pna ýÞS-п/кзамкнуто Дизъюнктивные и конъюктивные нормальные формы. СДНФ и СКНФ. Теорема о представлении булевой функции в виде СДНФ и СКНФ. Любая формула х или !х над стандартным базисом, где х – произвольная переменная, называется литералом. Пусть ~xi – литерал. Ф-ла видa ~x1/\~x2/\…/\~xk наз-ся элементарной конъюкцией ~x1\/~x2\/…\/~xk - элементарной дизъюнкцией (все переменные, входящие в ЭК и ЭД попарно различны) ДНФ от переменных х1…хn называется ф-ла вида K1\/K2\/…\/Km, где Ki, i=1,m – ЭК КНФ от переменных х1…хn называется ф-ла вида D1\/D2\/…\/Dm, где Di, i=1,m - ЭД Если в каждую ЭК входят все переменные х1…хn или их отрицания, то такая ДНФ называется совершенной ДНФ. Т-ма: Любая БФ, отличная от константы 0 (1) мб представлена формулой в виде СДНФ (СКНФ) Д-во (для первого): рассм некоторую БФ f, отличную от константы 0. Сформируем м-во С1f={~L | f(~L)=1}. Каждый набор из С1f называется конституентой единицы ф-ии f. Т.к. по усл ф-я не равно 0, м-воC1f не пусто. Каждому набору поставим в соответствие ЭК: ~L э C1f ->x1^L1…xn^Ln. Эта формула обращается в единицу только на наборе ~L и равно 0 на любом наборе B, отличном от L. Тогда искомая ф-ла им вид f=\/x1^L1…xn^Ln, L э C1f. Полное множество булевых функций. Теорема о доказательстве полноты множества путем представления его элементов формулами над полным множеством. М-во БФ назполным, если любая БФ в нём мб представлена ф-лой над ним. Т-ма: Пусть F – полн м-во БФ. Если любая функция из F мб представлена формулой над м-вом G, то м-воG также полное. Д-во: Пусть для люб f э Ff(x1…xn)=псиG(x1…xn) (мб предст как) 1. Пусть фи – некот ф-ла над F. Фи=х =>y будет формулой и над G. 2. Фи=с э F (пусть фи – некоторая константа из множества F, если она нам существует) Тогда по предположению существует G. 3. Пусть над м-вом F построена f(Ф1…Фn), где Фi – некоторая ф-ла над F. Согласно индуктивному предположению над каждой Фi существует эквивалентная ей ф-ла тетаi над множеством G. Тогда f(Ф1…Фn)=f(тета1…тетаn)=псиG. Поскольку в силу полноты любая БФ может быть представлена формулой над F, то эта же БФ мб представлена ф-лой над G. |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 283. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 L2 регулярно.
L2 регулярно. ,xiÎSsup
,xiÎSsup  £)
£) nÎN
nÎN = sup
= sup 
 = sup
= sup 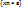
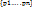 ее членов,т.е. согласно теор.,вычислить некоторую конечную сумму, которая всегда $.Таким образом, в кот.
ее членов,т.е. согласно теор.,вычислить некоторую конечную сумму, которая всегда $.Таким образом, в кот.