
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение коэффициента гидравлического сопротивления внутренней поверхности трубопровода
Потери напора по длине для труб постоянного диаметра определяются по формуле Дарси-Вейсбаха
где l — коэффициент гидравлического сопротивления (гидравлического трения); l — длина трубы; d — ее внутренний диаметр; u — средняя скорость потока. Входящий в нее коэффициент гидравлического сопротивления и является функцией числа Рейнольдса Rе и относительной шероховатости
где При ламинарном течении, а также и при турбулентном в зоне сравнительно небольших Rе, выступы шероховатости плавно обтекаются потоком жидкости, шероховатость не влияет на потерю напора и коэффициент гидравлического сопротивления зависит только от числа Рейнольдса. С увеличением Rе коэффициент Область, в которой Увеличение числа Рейнольдса приводит к тому, что от бугорков шероховатости начинают отрываться вихри. Это явление наступает тем раньше, чем больше шероховатость. Теперь сопротивление течению жидкости зависит не только от числа Рейнольдса, но и от шероховатости. Область, в которой При больших числа Рейнольдса коэффициент Область, в которой  При ламинарном течении (Rе < 2000) коэффициент гидравлического сопротивления находят то формуле Стокса:
Ламинарный режим бывает при перекачке вязких нефтей. Для вычисления
Обычно этой формулой пользуются при расчете нефтепроводов для нефти средней вязкости. В зоне квадратичного закона трения коэффициент гидравлического сопротивления определяется по формуле Никурадзе:
Альтшуль рекомендует пользоваться формулой Шифринсона:
где К — эквивалентная шероховатость, характеризующая суммарное влияние состояния внутренней поверхности стенки трубопровода на гидравлическое сопротивление. В формуле Никурадзе и во всех остальных приведенных ниже формулах величину
Квадратичного режима в нефтепроводах не бывает. Лишь приближенно иногда считают, что при квадратичном режиме могут перекачиваться светлые нефтепродукты. Квадратичный закон трения может быть в магистральных газопроводах. Для определения коэффициента гидравлического сопротивления в зоне смешанного трения применяются «универсальные» формулы. Их структура такова, что при малых числах Рейнольдса они обращаются в формулы
Если, здесь пренебречь стоящим в скобках вторым членом, то останется формула Никурадзе для квадратичного закона трения. Если же пренебречь первым членом получим формулу Прандтля для режима гладкого трения:
Результаты вычислений От этого недостатка свободны аналогичные формулы (дающие практически такие же результаты), предложенные Френкелем
Исаевым
Особой простотой отличается формула Альтшуля
При
Обобщенная формула Лейбензона
Формулы Стокса, Блазиуса и Никурадзе (а также и Шифринсона) имеют следующий общий вид:
где А и т — постоянные величины, т называется показателем режима движения жидкости. Подставив (6) в уравнение Дарси-Вейсбаха (5) и учитывая
где
Формула Лейбензона широко применяется в тех случаях, когда зависимость
На графике Последнее обстоятельство исключает возможность использования формулы Лейбензона в области смешанного трения. Это большой недостаток, так как область смешанного трения охватывает широкий интервал чисел Рейнольдса, при которых обычно ведутся перекачки маловязких нефтей и светлых нефтепродуктов. Однако ценой некоторой потери в точности расчетов этот недостаток может быть устранен. Отметим на графике Теперь проведем через точки 1-й 2 прямую. Ее уравнение приводится к виду
Приняв
получим
Очевидно, замена кривой
Рис. 1. Замена Кривой
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 371. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1)

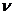 —кинематическая вязкость, перекачиваемой нефти, Q — объемный расход, е — абсолютная шероховатость стенок трубопровода.
—кинематическая вязкость, перекачиваемой нефти, Q — объемный расход, е — абсолютная шероховатость стенок трубопровода.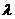 уменьшается.
уменьшается. называется областью гладкого трения.
называется областью гладкого трения. называется областью смешанного трения. Здесь с увеличением Rе его влияние на
называется областью смешанного трения. Здесь с увеличением Rе его влияние на  , называется областью совершенно шероховатого трения или областью квадратичного режима движения, так как здесь
, называется областью совершенно шероховатого трения или областью квадратичного режима движения, так как здесь 



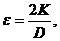
 .
.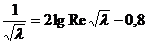 .
. ,
,
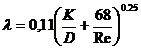 .
.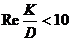 она практически совпадает с формулой Блазиуса, а при
она практически совпадает с формулой Блазиуса, а при 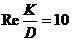 — с формулой Шифринсона;
— с формулой Шифринсона;  — границей между областями смешанного и совершенно шероховатого трения.
— границей между областями смешанного и совершенно шероховатого трения. , (2)
, (2)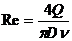 , получим обобщенную формулу Лейбензона:
, получим обобщенную формулу Лейбензона: ,
, .
. от Q должна быть выражена в явном виде. Величины т, А и
от Q должна быть выражена в явном виде. Величины т, А и  имеют следующие значения:
имеют следующие значения:


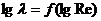 зависимость (2) для указанных в таблице режимов течения выглядит в виде прямых линий, тангенс угла наклона которых к оси lgRe равен т. В области смешанного трения, где
зависимость (2) для указанных в таблице режимов течения выглядит в виде прямых линий, тангенс угла наклона которых к оси lgRe равен т. В области смешанного трения, где  , линия
, линия  , и цифрой 2 точку на прямой Шифринсона, где
, и цифрой 2 точку на прямой Шифринсона, где  (границы области смешанного трения). Подставив Re1 в формулу Блазиуеа, а Re2 в формулу Шифринсона, найдем
(границы области смешанного трения). Подставив Re1 в формулу Блазиуеа, а Re2 в формулу Шифринсона, найдем  и
и  — ординаты точек 1 и 2.
— ординаты точек 1 и 2. .
. ,
, . (3)
. (3)