
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение задачи симплекс-методом ⇐ ПредыдущаяСтр 2 из 2 Первым шагом нужно выбрать количество базисных переменных в базисе и определить переменные, которые войдут в первое базисное решение. Имеющиеся уравнения условий преобразуем к виду: а11х1 + а12х2 + а13х3 + а14х4 + а15х5 = b1. Для первого условия получаем: 1х1 + 1х2 + 0х3 + 0х4 + 0х5 = 1 Для второго: (-1)х1 + 0х2 + 1х3 + 1х4 +0х5 = 0 Для третьего: 0х1 + 1х2+ 1х3 + 0х4 + (-1)х5 = 0 Для четвертого: 0х1+ 0х2 + 0х3 + 1х4 + 1х5 = 1 Затем составляем матрицу коэффициентов, которая будет выглядеть таким образом:
Базисных переменных в базисе будет столько, сколько линейно-независимых уравнений. Поэтому мы находим ранг матрицы. Для этого приводим матрицу к ступенчатому виду, используя элементарные преобразования. 1) Ко второй строке прибавляем первую строку.
2) От третьей строки отнимаем вторую строку.
3) Третью строку делим на (-1).
4) От четвертой строки отнимаем третью строку.
Так как ненулевых строк 3, то ранг матрицы равен 3.Но у нас 4 уравнения условий. Значит, необходимо вычеркнуть одно из них и не брать его во внимание. Допустим, вычеркнем третье уравнение. Тогда матрица коэффициентов будет выглядеть таким образом:
Теперь мы можем начать составление симплекс-таблицы. Первая интерация:
←
↑ Вторая интерация:
 ←
↑
Третья интерация:
Найдено оптимальное решение: Мы видим, что кратчайший путь пролегает через узлы 1,2 и 4 по рёбрам 1 и 4.
Рис.3.Найденный кратчайший путь
Использованная литература
Ларин Р.М., Плясунов А.В., Пяткин А.В.. Методы оптимизации. Примеры и задачи: Учеб. Пособие / Новосиб. ун-т. Новосибирск, 2003. 115 с. Гасс С.И.. Линейное программирование (методы и приложения) / М.: Гос. Изд-во физ- мат. лит-ры, 1961. 303 с. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 215. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
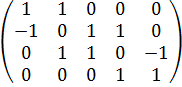


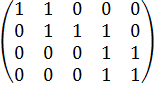


 .
. Найдём кратчайший путь на сети, подставив значения переменных в функцию:
Найдём кратчайший путь на сети, подставив значения переменных в функцию: