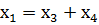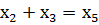Постановка задачи линейного программирования

Введение

Задача о кратчайшем пути - задача поиска самого короткого пути между двумя точками, в которой минимизируется сумма весов рёбер, составляющих путь. В нашей задаче мы рассмотрим путь как сеть трасс. Совершенно не важно, какой тип у этих трасс. Они могут быть воздушными, автомобильными, морскими, велосипедными или просто пешими.Заданная сеть представлена на рисунке ниже.

Рис. 1. Заданная сеть

Стрелки показывают, в каком направлении может двигатьсяобъект на каждом участке сети.

Задача данного типа часто используется в системе управления воздушным движением, так как её решение позволяет находить наиболее кратчайшие обходные маршруты и оптимизировать совместное использование воздушного пространства рейсами государственной и гражданской авиации.

Данную задачу необходимо решать, применяя метод линейного программирования. Дадим определение данному методу.

Линейное программирование — математическая дисциплина, изучающая теории и методы решения экстремальных задач на множествахвекторного пространства, задаваемых системами линейных уравнений и неравенств.

Далее необходимо подобрать наиболее удобную математическую модель, чтобы описать данную задачу. Такой моделью будет граф.

Граф - совокупность множества вершин и наборов пар вершин.

В данной задаче места пересечения трасс - узлы графа, а сами трассы - рёбра графа. При этом мы получаем математическую модель, представленную ниже.

Рис. 2. Модель сети

Следует учесть, что графы бывают ориентированными и не ориентированными. По рисунку видно, что вершины графа соединены дугами, соответственно, переход из одного узла графа в другой возможен только в единственно возможном направлении. Это означает, что данный граф являетсяориентированным.

В противном случае вершины графа были бы соединены рёбрами, и граф являлся бы неориентированным.В этом случае необходимо представить каждый участок в виде двух дуг, направленных в разные стороны и соединяющих одни и те же вершины. Такой вид решения не распространяется на данную задачу.

Существует несколько методов решения задачи о кратчайшем пути. Например, алгоритм нидерландского учёного Дейкстры. Но в этой работе мы рассматриваем метод линейного программирования, а конкретно - симплекс-метод. Дадим определение данному методу.

Симплекс-метод — алгоритм решения задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.

Для рассмотрения решения задачи сиплекс-методом удобно данную нам задачу о кратчайшем пути свести к задаче о потоке минимальной стоимости. В качестве коэффициентов стоимости нужно взять длины рёбер графа. Составим таблицу исходных данных, пронумеровав рёбра, как на рисунке 2:

Коэффициент, задающий длину i-того ребра, обозначим как С_i.

Переменную, которой соответствует коэффициент С_i, обозначим x_i. Переменные показывают, какой поток проходит по каждому ребру графа.

Постановка задачи линейного программирования

Воспользуемся законом о сохранении потока: поток, приходящий в узел, численно равен потоку, выходящему из него.

Рассмотрим каждые узлы отдельно, обратившись для этого к модели сети.

Первый узел:

Второй узел:

Третий узел:

Четвёртый узел:

Таким образом, система уравнений будет выглядеть так:

А сама функция цели имеет вид: 42x₁ + 48x₂+ 36x₃ + 33x₄ + 41x₅ → min

АХ = b, где Х и b – вектор-столбцы, аА – матрица размерности m × n.