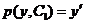Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Часть 2. Уравнения высших порядков допускающие понижение порядка. ⇐ ПредыдущаяСтр 2 из 2 Далее перейдем к уравнениям более высокого порядка. Дифференциальным уравнением порядка Частным решением дифференциального уравнения называется любая функция Задачей Коши для дифференциального уравнения порядка
удовлетворяющего условиям
Известно, что при определенных условиях задача Коши имеет решение и при том единственное. Общим решением дифференциального уравнения 1. При любом наборе произвольных постоянных 2. Для любых начальных условий задачи Коши
В контрольной работе присутствуют два типа уравнений, допускающих понижение порядка. Первый тип -этоуравнения, которые явно не содержат неизвестную функцию и ее производные до некоторого порядка . Пусть дано уравнение порядка n вида то есть в данное уравнение явно не входят неизвестная функция и производные этой функции до порядка k-1 включительно. Введем новую неизвестную функцию  Пример. При x>0 найти общее решение дифференциального уравнения Это уравнение явно не содержит y и Уравнение для определения функции Так как Обозначим Ответ: Пример. Найти общее решение дифференциального уравнения Данное уравнение не содержит явно неизвестную функцию Полученное уравнение является линейным дифференциальным уравнением первого порядка. Будем искать
Выберем функцию Найдем функцию Тогда Определим
=
Так как
Ответ:
Второй тип уравнений, допускающих понижение порядка, - это уравнения, которые явно не содержат независимую переменную Будем искать производную Подставляя Полученное уравнение является уравнением первого порядка для функции Замечание. При изложенном методе могут быть потерянны решения Пример. Найти решение задачи Коши: Будем искать Полученное для Ответ: Пример. Найти решение задачи Коши: Будем искать Полученное для Ответ: Пример. Решить задачу Коши Будем искать Полученное для Определим произвольную постоянную С. Так как при Следовательно, Ответ: Схема исследования приведенных уравнений сведена в таблицу 2.
Таблица 2. |
||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 136. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
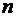 , разрешенным относительно старшей производной, называется дифференциальное уравнение вида
, разрешенным относительно старшей производной, называется дифференциальное уравнение вида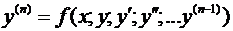 .
. , при подстановке которой в дифференциальное уравнение, оно превращается в тождество.
, при подстановке которой в дифференциальное уравнение, оно превращается в тождество.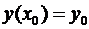 ,
,  ,
,  ,…,
,…,  .
. , где
, где  - произвольные постоянные, удовлетворяющая условиям:
- произвольные постоянные, удовлетворяющая условиям: существует такой набор значений произвольных постоянных
существует такой набор значений произвольных постоянных 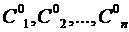 , что выполнены условия
, что выполнены условия  ,
,  ,…….,
,……., .
. ,
, . Производные функции
. Производные функции  выразятся через производные функции
выразятся через производные функции  следующим образом:
следующим образом:  ,…,
,…,  . Подставляя в исходное уравнение, получаем
. Подставляя в исходное уравнение, получаем  . Полученное уравнение для функции
. Полученное уравнение для функции  =
=  .
. . Обозначим
. Обозначим  . Тогда:
. Тогда:  . Подставляя в исходное уравнение, получаем
. Подставляя в исходное уравнение, получаем .
. ;
;  ;
;  ;
;  ;
; 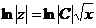 ;
;  ;
;  .
. =
=  . Тогда
. Тогда  .
.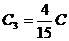 .
. , где
, где  - произвольные постоянные.
- произвольные постоянные. .
. . Введем новую неизвестную функцию
. Введем новую неизвестную функцию 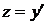 . Тогда
. Тогда  и уравнение преобразуется к виду
и уравнение преобразуется к виду .
. в виде
в виде 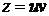 . Тогда
. Тогда 
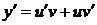 . Подставляя
. Подставляя 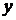 и
и  в исходное уравнение, получаем:
в исходное уравнение, получаем: ;
; 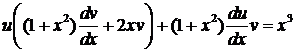 .
.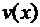 из условия
из условия  . Уравнение для функции
. Уравнение для функции  ;
;  ;
; 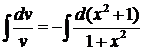 ;
;  ,
,  .
. :
: ;
;  ;
;  .
. =
= 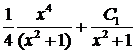 .
.
 =
= =
= .
. является так же произвольной постоянной, то окончательный ответ может быть записан в виде
является так же произвольной постоянной, то окончательный ответ может быть записан в виде .
. . (Мы будем рассматривать только уравнения второго порядка, однако предложенный метод применим и для уравнений более высокого порядка.) Пусть дано уравнение вида
. (Мы будем рассматривать только уравнения второго порядка, однако предложенный метод применим и для уравнений более высокого порядка.) Пусть дано уравнение вида .
. в виде
в виде  , где
, где  - неизвестная функция. Тогда
- неизвестная функция. Тогда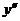 =
=  =
=  =
= 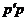 .
.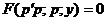 .
. , то есть
, то есть  . Поэтому такие решения рекомендуется выписывать отдельно.
. Поэтому такие решения рекомендуется выписывать отдельно. ,
,  ,
,  .
. . Подставляя
. Подставляя 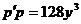 .
. ,
, 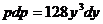 ,
,  ,
,  . Определим произвольную постоянную С. Так как при
. Определим произвольную постоянную С. Так как при 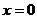 имеем
имеем  при
при  . Тогда 32=32+С, С=0. Следовательно,
. Тогда 32=32+С, С=0. Следовательно,  или
или 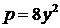 . Знак плюс при извлечении корня выбран потому, что
. Знак плюс при извлечении корня выбран потому, что  . Найдем его решение:
. Найдем его решение:  . Поскольку
. Поскольку 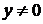 , то
, то  ,
, 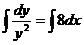 ,
,  ,
,  . Так как
. Так как 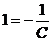 ,
,  . Следовательно,
. Следовательно,  .
. ,
,  ,
,  .
. в виде
в виде 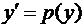 . Тогда
. Тогда  . Подставляя
. Подставляя  и
и 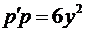 .
. уравнение является уравнением с разделяющимися переменными. Найдем его решение:
уравнение является уравнением с разделяющимися переменными. Найдем его решение:  ,
,  ,
,  ,
,  . Определим произвольную постоянную С. Так как по условию при
. Определим произвольную постоянную С. Так как по условию при  имеем
имеем 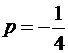 при
при  . Тогда
. Тогда  =
=  или
или  . Знак минус при извлечении корня выберем потому, что
. Знак минус при извлечении корня выберем потому, что  определяем из уравнения
определяем из уравнения  . Найдем его решение:
. Найдем его решение:  ,
,  ,
,  ,
,  ,
,  . Так как
. Так как  ,
,  . Следовательно,
. Следовательно,  .
. ,
,  ,
,  .
. .
.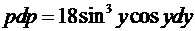 ,
,  ,
, 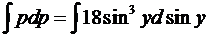 ,
,  .
. имеем
имеем  при
при 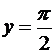 . Тогда
. Тогда  , С=0. Следовательно,
, С=0. Следовательно,  или
или  . Знак плюс при извлечении корня выберем плюс потому, что
. Знак плюс при извлечении корня выберем плюс потому, что  . Неизвестную функцию
. Неизвестную функцию  . Найдем его решение:
. Найдем его решение: 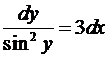 ,
,  ,
,  . Так как
. Так как  ,
,  .
. .
.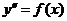
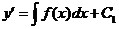


 ,
,  Решаем уравнение первого порядка
Решаем уравнение первого порядка 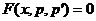 .
Решаем уравнение с разделяющимися переменными
.
Решаем уравнение с разделяющимися переменными 
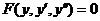
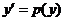 ,
,  Решаем уравнение первого порядка
Решаем уравнение первого порядка  .
Решаем уравнение с разделяющимися переменными
.
Решаем уравнение с разделяющимися переменными