
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения с разделяющимися переменными.Стр 1 из 2Следующая ⇒ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Московский государственный университет Приборостроения и информатики
Кафедра высшей математики ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (решение задач) Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.
Москва 2005
Излагаются основные методы решения обыкновенных дифференциальных уравнений. Пособие является частью пособия для заочного отделения (автор Антонова И.И., МГУПИ), содержащей уравнения с разделяющимися переменными, однородные уравнения, линейные уравнения первого порядка, уравнения Бернулли, некоторые уравнения высших порядков.
Часть 1. Дифференциальные уравнения первого прядка. Прежде чем перейти к решению конкретных типов задач, напомним некоторые общие положения, касающиеся дифференциальных уравнений первого порядка. Дифференциальным уравнением первого порядка, разрешенным относительно производной, называется соотношение вида Частным решением дифференциального уравнения называется любая функция Задачей Коши для дифференциального уравнения первого порядка называется задача отыскания решения дифференциального уравнения
удовлетворяющего условиям, Известно, что если в некоторой области функция  Общим решением дифференциального уравнения первого порядка в некоторой области называется совокупность функций 1.При любом значении произвольной постоянной С функция 2. Для любых начальных условий задачи Коши Если общее решение
Уравнения с разделяющимися переменными. Определение. Уравнением с разделяющимися переменными называется уравнение, которое может быть записано в виде: Можно предложить следующую схему решения этого уравнения. Разделяем переменные, то есть уравнение переписываем в виде: Интегрируя левую и правую части этого уравнения, получаем: где С – произвольная постоянная. Полученное соотношение является общим интегралом исходного дифференциального уравнения. Замечание. Если функция
Пример. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде
Для того, что бы убедиться, что данное уравнение действительно является уравнением с разделяющимися переменными, выразим Тогда Интегрируя правую и левую части, получаем Приведем схему вычисления интеграла: После вычисления интегралов имеем: Ответ: Пример. Найти общий интеграл дифференциального уравнения. Уравнение запишем в виде Тогда В случае Интегрируя правую и левую части, получаем Приведем схему вычисления интеграла
После вычисления интегралов имеем: Потенцируя данное выражение, получаем Ответ:
Пример. Найти общий интеграл дифференциального уравнения
Тогда Интегрируя правую и левую части, получаем После вычисления интегралов имеем: Ответ:
Пример. Найти общий интеграл дифференциального уравнения
Поясним, что такая запись подразумевает под Перенесем выражения, содержащие Разделяем переменные Интегрируя правую и левую части, получаем Приведем схему нахождения интеграла
После вычисления интегралов имеем
Потенцируя полученное выражение, имеем
Ответ:
Однородные уравнения. Определение. Однородным уравнением называется дифференциальное уравнение первого порядка, которое может быть записано в виде: Можно предложить следующий метод его решения. Неизвестную функцию Данное уравнение представим в виде Полученное уравнение является уравнением с разделяющимися переменными для функции Пример. Найти общий интеграл дифференциального уравнения Данное уравнение является однородным. Будем искать неизвестную функцию Полученное уравнение преобразуем к виду Разделяем переменные Интегрируем правую и левую части (В нашем случае произвольную постоянную удобнее обозначить не С, а Потенцируя, имеем Избавляясь от знака модуля, получаем Поскольку Заметим, что в уравнении Решение Ответ: Пример. Найти общий интеграл дифференциального уравнения. Поскольку данное уравнение является однородным, то неизвестную функцию Полученное уравнение преобразуем к виду Разделяем переменные Интегрируем правую и левую части Вычисляя интегралы в правой и левой частях уравнения, получаем Поскольку
Ответ: Пример. Найти общий интеграл дифференциального уравнения Данное уравнение является однородным. Будем искать неизвестную функцию Данное уравнение преобразуем к виду
Поскольку правая часть не равна нулю ни при каких значениях
Интегрируя, имеем
Приведем схему нахождения интеграла
После вычисления интегралов получаем
Поскольку
Ответ:
3. Линейные дифференциальные уравнения первого порядка. Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое может быть записано в виде где Р(х) и Q(х) – известные функции. Можно предложить следующий метод решения этого уравнения. Неизвестную функцию y(x) будем искать в виде Полученное уравнение преобразуем к виду Подберем функцию (Это уравнение для определения функции где С – произвольная постоянная. Тогда общее решение Пример. Найти решение задачи Коши: Вначале найдем общее решение этого уравнения. Будем искать Выберем функцию Найдем функцию Тогда общее решение исходного уравнения имеет вид Произвольную постоянную С определим из условия
Ответ: Пример. Найти общее решение дифференциального уравнения Данное дифференциальное уравнение является линейным дифференциальным уравнением первого порядка. Будем искать Выберем функцию Найдем функцию Тогда общее решение исходного уравнения имеет вид Ответ: Пример. Найти решение задачи Коши Данное дифференциальное уравнение является линейным дифференциальным уравнением первого порядка. Будем искать
Выберем функцию Найдем функцию Тогда общее решение исходного уравнения имеет вид Определим произвольную постоянную С. Так как Ответ:
4. Уравнение Бернулли. Определение. Уравнением Бернулли называется дифференциальное уравнение первого порядка, которое может быть записано в виде Можно предложить следующий метод решения этого уравнения. Неизвестную функцию y(x) будем искать в виде Полученное уравнение преобразуем к виду Подберем функцию (Это уравнение для определения функции Тогда для определения Это уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными и способ его решения изложен ранее. Пример. Найти решение задачи Коши: Вначале найдем общее решение этого уравнения. Будем искать Ответ:
Пример. Найти решение задачи Коши: Данное уравнение является уравнением Бернулли. Будем искать Ответ: Пример. Найти решение задачи Коши: Вначале найдем общее решение этого уравнения. Будем искать
Функцию Интегрируем правую и левую части полученного соотношения
Приведем схему вычисления полученных интегралов.
Для вычисления
Подставляя полученные интегралы в исходное выражение, получаем Используя начальные условия задачи Коши, определим С. Так как Тогда имеем Ответ: Типы рассмотренных уравнений и методы их решения сведены в таблицу 1. Приведем решение еще одного уравнения с использованием указанной таблицы. Пример. Решить уравнение 1.Переменные не разделяются, так как 2.Подставим 3.Выделим линейную часть вида 4.Поменяем ролями функцию и аргумент. Разделим уравнение на Пусть
Ответ:
Таблица 1.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 159. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||


 .
. , при подстановке которой в дифференциальное уравнение, оно превращается в тождество.
, при подстановке которой в дифференциальное уравнение, оно превращается в тождество. при
при  .
. непрерывна вместе со своей частной производной
непрерывна вместе со своей частной производной  , то в этой области задача Коши имеет решение и при том единственное.
, то в этой области задача Коши имеет решение и при том единственное. (С – произвольная постоянная), удовлетворяющая двум условиям:
(С – произвольная постоянная), удовлетворяющая двум условиям: , такое что
, такое что 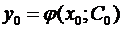 .
. , то такое соотношение называется общим интегралом дифференциального уравнения первого порядка. Далее рассмотрим методы решения тех классов дифференциальных уравнений первого порядка, которые представлены в контрольной работе.
, то такое соотношение называется общим интегралом дифференциального уравнения первого порядка. Далее рассмотрим методы решения тех классов дифференциальных уравнений первого порядка, которые представлены в контрольной работе. .
.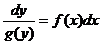 .
. ,
, равна нулю в точках
равна нулю в точках  , то функции
, то функции  ,
,  ,….,
,….,  являются решениями исходного уравнения. При изложенном методе такие решения могут быть потеряны, поэтому их рекомендуется выписать отдельно.
являются решениями исходного уравнения. При изложенном методе такие решения могут быть потеряны, поэтому их рекомендуется выписать отдельно. y(x,y)=C).
y(x,y)=C). .
. . Имеем
. Имеем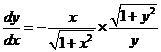
 ,
,  . Заметим, что
. Заметим, что  . Разделяем переменные:
. Разделяем переменные: .
.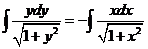 .
. =
=  .
. .
. .
. .
. .
. ,
, 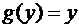 . Заметим, что
. Заметим, что  при
при  . Следовательно, функция
. Следовательно, функция  разделяем переменные:
разделяем переменные: .
. .
.
 ,
, 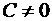 .
. . Отметим, что решение
. Отметим, что решение  .
. ,
,  . Заметим, что
. Заметим, что  . Разделяем переменные:
. Разделяем переменные: .
. .
. .
. .
.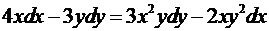 .
. дифференциал независимой переменной, под
дифференциал независимой переменной, под 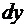 - дифференциал неизвестной функции (
- дифференциал неизвестной функции (  ).
). .
. .
. .
. .
. .
. .
. .
. будем искать в виде
будем искать в виде  , где
, где  - неизвестная функция. Тогда
- неизвестная функция. Тогда  . Подставляя
. Подставляя  и
и  в исходное уравнение, получаем:
в исходное уравнение, получаем: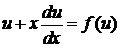 .
. .
. .
. .
. .
. .
. +
+ 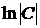 .
.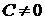 . Вычисляя интегралы в правой и левой частях уравнения, получаем
. Вычисляя интегралы в правой и левой частях уравнения, получаем .
. .
. .
. , то полученное соотношение может быть представлено в виде
, то полученное соотношение может быть представлено в виде .
. , выражение
, выражение  при
при 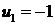 ,
,  . Следовательно, функции
. Следовательно, функции 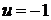 и
и  являются решениями дифференциального уравнения для неизвестной функции
являются решениями дифференциального уравнения для неизвестной функции  и
и  являются решениями исходного дифференциального уравнения.
являются решениями исходного дифференциального уравнения. .
. .
.

 .
. .
. .
.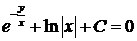 , где С – произвольная постоянная.
, где С – произвольная постоянная. .
. в виде
в виде  . Тогда
. Тогда  . Подставляя
. Подставляя  и
и  в исходное уравнение, получаем:
в исходное уравнение, получаем: .
. .
. , то, разделяя переменные, получаем
, то, разделяя переменные, получаем .
. +С.
+С.
 .
. .
. , то выражение записываем в виде
, то выражение записываем в виде .
. .
.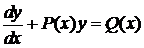 ,
, , где
, где  - некоторая функция, выбранная специальным образом. (Способ выбора
- некоторая функция, выбранная специальным образом. (Способ выбора  равна:
равна: 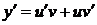 . Подставляя
. Подставляя 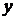 и
и  +
+  .
. .
. .
. . Из этого уравнения при известной функции
. Из этого уравнения при известной функции  ,
,
 ,
,  .
. и
и 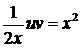 ;
; 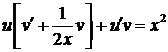 .
. . Уравнение для функции
. Уравнение для функции  ;
;  ;
;  ;
;  .
. ;
; 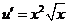 ;
;  ;
; 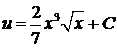 .
. .
. ;
;  .
.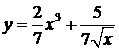 .
.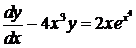 .
. ;
;  .
. . Уравнение для функции
. Уравнение для функции  ;
;  ;
;  ;
; 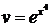 .
. ;
;  ;
;  ;
;  .
. .
.
 ,
,  .
. . Тогда
. Тогда  . Подставляя
. Подставляя  ;
;  .
.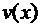 из условия
из условия  . Уравнение для функции
. Уравнение для функции  ;
;  ;
;  ;
;  ,
,  .
. :
: ;
;  ;
;  .
. .
. ,
, 

 .
. 
 +
+  .
. .
. .
.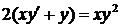 ,
,  .
.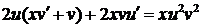 . Функцию
. Функцию  ;
;  ;
;  ;
;  ;
; 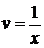 . Определим
. Определим  ;
; 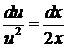 ;
;  +С;
+С;  ;
;  . Следовательно, общее решение имеет вид
. Следовательно, общее решение имеет вид  . Из условия
. Из условия  ;
;  .
. .
. ,
, 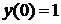 .
. . Функцию
. Функцию  ;
;  ;
;  ;
;  ;
;  . Определим
. Определим 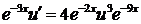 ;
; 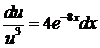 ;
;  +С;
+С;  ;
;  .( Знак плюс при извлечении квадратного корня выбран исходя из начальных условий). Следовательно, общее решение имеет вид
.( Знак плюс при извлечении квадратного корня выбран исходя из начальных условий). Следовательно, общее решение имеет вид  . Из условия
. Из условия  ;
; 
 .
.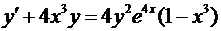 ,
,  .
. ;
;  .
. ,
,  ;
;  ;
;  ;
;  . Определим
. Определим  ;
;  ;
;  .
. 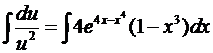 .
. .
. сделаем замену переменных
сделаем замену переменных  ,
,  ,
,  . Тогда получаем
. Тогда получаем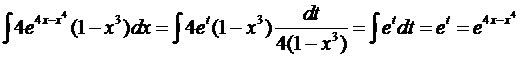

 ,
, 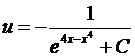 . Следовательно , общее решение имеет вид
. Следовательно , общее решение имеет вид 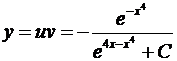 .
.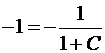 , С=0.
, С=0. .
.
 .
.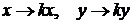 в
в  и
и 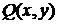 , получим
, получим  . Из скобки
. Из скобки  невозможно вынести
невозможно вынести 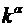 , т.е. функция
, т.е. функция  не является однородной. Вывод: это не однородное уравнение.
не является однородной. Вывод: это не однородное уравнение. . Делим уравнение на
. Делим уравнение на  . Тогда:
. Тогда:  ;
;  , но
, но  . Линейная часть относительно
. Линейная часть относительно 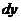 и учтем, что
и учтем, что  . Тогда:
. Тогда:  . В этом дифференциальном уравнении легко просматривается линейная относительно
. В этом дифференциальном уравнении легко просматривается линейная относительно  и
и  часть:
часть:  . В правой части этого соотношения видим
. В правой части этого соотношения видим  и делаем вывод, что это уравнение относится к типу уравнений Бернулли относительно
и делаем вывод, что это уравнение относится к типу уравнений Бернулли относительно  . Тогда:
. Тогда:  ;
;  .
. ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
; 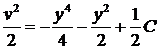 ;
;  . Ответ удобно искать в виде:
. Ответ удобно искать в виде:  ;
;  .
. .
.

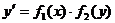

 , преобразовать уравнение к виду
, преобразовать уравнение к виду  и интегрировать обе части
и интегрировать обе части

 и
и 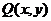 должны быть однородными функциями одного измерения:
должны быть однородными функциями одного измерения:



 приведет уравнение к уравнению с разделяющимися переменными. При этом
приведет уравнение к уравнению с разделяющимися переменными. При этом  или
или 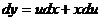
 или
или 
 (или
(или  )
)
 ,
, 