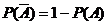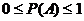Аксиоматическое определение вероятности.

Необходимость формально логического обоснования теории вероятностей, её аксиоматического построения возникла в связи с развитием самой теории вероятностей как математической науки и её приложений в различных областях.

Впервые идея аксиоматического построения вероятностей была высказана российским академиком Бернштейном (Бернштейн Сергей Натанович 1880-1968), исходившим из качественного сравнения событий по их большей или меньшей вероятности.

В начале 30-х годов прошлого столетия академик Колмогоров (Колмогоров Андрей Николаевич 1903-1987) разработал иной подход, связывающий теорию вероятностей с современной метрической теорией функций и теорией множеств.

Приведём систему аксиом, предложенную Колмогоровым.

Аксиоматическое определение.

Вероятностью события А называется число Р(А), которое сопоставляется каждому событию рассматриваемого множества событий и которое удовлетворяет следующим аксиомам:

Аксиома 1: (неотрицательности) Вероятность любого события неотрицательна.

Аксиома 2: (нормировки) Вероятность достоверного события равна 1.

Аксиома 3: (сложения) Вероятность суммы любого конечного множества попарно несовместных событий равна сумме их вероятностей.

Аксиома 4: (однозначности) Эквивалентные события имеют равные вероятности.

Следствия из аксиом:

1. Вероятность невозможного события равна 0.

2. Вероятность события противоположного событию А

3. Вероятность любого события

Аксиомы теории вероятностей позволяют вычислить вероятности любых событий через вероятности элементарных событий.

Вопрос о том, откуда берутся вероятности элементарных событий, при аксиоматическом построении теории вероятностей не рассматривается. На практике они определяются с помощью классического, статистического, геометрического определений.

Таким образом, аксиоматическое определение:

· Обобщает классическое, статистическое, геометрическое определения.

· Постулирует существование вероятности как объективно существующей характеристики реальных событий, не зависящей ни от самого исследователя, ни от количества проведённых им экспериментов.

Теоремы сложения и умножения вероятностей.

Как правило, для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Применяя косвенные методы, мы всегда в той или иной форме пользуемся основными теоремами теории вероятностей – теоремами сложения и умножения вероятностей. Эти теоремы могут быть доказаны только для событий, сводящихся к схеме случаев. Для остальных событий они принимаются аксиоматически.