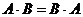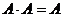Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Различные определения вероятности.Стр 1 из 3Следующая ⇒ ТЕМА 1. СЛУЧАЙНЫЕ СОБЫТИЯ.
Комбинаторика– раздел математики, изучающий методы решения задач на подсчёт числа различных комбинаций. При решении комбинаторных задач применяют следующие правила. Правило суммы (ИЛИ). Если некоторый объект А может быть выбран из совокупности объектов Пример. В ящике 300 деталей. Известно, что 150 из них – 1-го сорта, 120 – 2-го, а остальные – 3-его сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта? Решение. Деталь 1-го сорта может быть извлечена 150 способами, 2-го сорта – 120 способами. Тогда 1-го или 2-го сорта: 150 + 120 = 270 способами. Правило произведения (И). Если некоторый объект А может быть выбран из совокупности объектов Пример. В студенческой группе 25 человек. Сколько существует способов выбрать старосту и заместителя? Решение. Старостой может быть выбран любой из 25 студентов, а его заместителем – любой из оставшихся 24 человек. Тогда общее число способов выбора старосты и заместителя: Выборки без повторений. Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества из k элементов ( Размещениями из n элементов по kназывают комбинации k элементов, составленные из n различных элементов, которые отличаются либо составом элементов, либо порядком их расположения.  Число размещений из n элементов по k обозначается
Пример. Расписание одного дня состоит из 5 пар. Определить число вариантов расписания при выборе из 11 дисциплин. Решение. Если комбинации из n элементов по k отличаются только составом элементов, то их называют сочетаниями из n элементов по k. Обозначают
Пример. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия? Решение. Свойства сочетаний. 1. 2. Перестановками из n элементов называют комбинации, составленные из n различных элементов, которые отличаются только порядком расположения этих элементов. Обозначают
Пример. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьёвки при этом возможно? Решение. Из приведённых определений следует: Выборки с повторениями. Если в выборках (размещениях, сочетаниях, перестановках) некоторые из элементов (или все) могут оказаться одинаковыми, то такие выборки называются выборками с повторениями. Число размещений из n элементов по k с повторениями равно:
Пример. Сколько четырёхзначных чисел можно образовать из нечётных цифр, если цифры могут повторяться? Решение. Нечётные цифры 1, 3, 5, 7, 9. Тогда : Число сочетаний из n элементов по k с повторениями равно:
Пример. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены одинаковые призы? Решение. Так как призы одинаковые, то каждый из вариантов распределения призов представляет комбинацию 5 фильмов из 10, отличающуюся от других только составом фильмов, причём одни и те же фильмы могут повторяться. Тогда: Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется
Пример. Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза? Решение. Каждое семизначное число отличается от другого порядком следования цифр, то есть является перестановкой из 7 элементов с повторениями 3, 2 и 2. Тогда:
Алгебра событий.
На практике часто встречаются такие ситуации, когда исход проводимого нами опыта (эксперимента, испытания) нельзя предсказать заранее с полной уверенностью. Например, невозможно предсказать, какая сторона выпадет при бросании монеты, выпадет ли выигрыш на лотерейный билет с таким-то номером, совпадут ли дни рождения у двух наугад выбранных людей и т.д. Во всех подобных ситуациях мы вынуждены считать результат опыта зависящим от случая, рассматривать его как случайное событие. Случайным событием (возможным событием) называется любой факт, который в результате опыта (эксперимента, испытания) может произойти или не произойти. Событие – не какое-нибудь происшествие, а лишь возможный исход (результат) опыта. События обозначают прописными буквами: А, В, С,… Понятие события – одно из основных понятий теории вероятностей. Если наступление события возможно в опытах, которые можно повторять неограниченное число раз, то такие события называются массовыми.Теория вероятностей занимается изучением закономерностей, присущих массовым случайным событиям. Событие называется достоверным, если в результате опыта оно обязательно должно произойти. Обозначается – U. Невозможноесобытие – событие, которое никогда не наступит при осуществлении данного опыта. Обозначается – V. Пример. Опыт – подбрасывание игральной кости. Выпадение целого числа очков – достоверное событие. Выпадение 0 – невозможное событие. События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании. В противном случае события называются совместными. Пример. Получение студентом на экзамене оценок «отлично», «хорошо», «удовлетворительно» по одной дисциплине – несовместные события, а по трём дисциплинам – совместные события. События называются равновозможными, если условия их появления одинаковы, ни одно из них не является более возможным, чем другое. Пример. Опыт – подбрасывание монеты. Выпадение «Г» или «Ц» - равновозможные события. Группа несовместных равновозможных событий называется полной группой событий, если в результате опыта наступает обязательно одно и только одно событие этой группы. Пример. Опыт – подбрасывание кубика. События
Если при каждом испытании, при котором происходит событие А, происходит и событие В, то говорят, что событиеА влечёт за собой событие В, и обозначают Пример. Опыт – подбрасывание кубика. А – выпадение чётного числа очков, В – выпадение числа очков Очевидно, что для любого события А: Если Операции над событиями. Событием противоположным событию А ( отрицанием А, не А) называется такое событие Пример. Опыт – подбрасывание монеты. Выпадение «Г» или «Ц» - противоположные события. Противоположные события частный случай событий, образующих полную группу. Свойства: 1. 2. 3. Суммой событий А и В (или конечного числа событий) называется такое событие А+В (А или В), которое происходит тогда и только тогда, когда происходит хотя бы одно из этих событий. Пример.
Свойства: 1. A + U = U 2. A + V = A 3. A + 4. A + A = A 5. A + B = B + A 6. (A + B) + C = A + (B + C) 7. Если 8. Для полной группы событий Произведением событий А и В (или конечного числа событий) называется такое событие Пример. Опыт – подбрасывание кубика. А – выпадение чётного числа очков. В – выпадение числа очков, кратных 3. Тогда Свойства: 1. 2. 3. 4. 5. 6. 7. 8. 9. Если Разностью двух событий А и В называется такое событие А-В (А без В), которое происходит тогда и только тогда, когда событие А произойдёт, а событие В не произойдёт. Пример. Опыт – подбрасывание кубика. А – выпадение чётного числа очков. В – выпадение «2». Тогда А-В – выпадение «4», «6». Свойства: 1. А - 2. А - U = V 3. А - V = А
Различные определения вероятности.
Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определённое число, которое тем больше, чем более возможно событие. Такое число мы назовём вероятностью события. Таким образом, вероятность события есть численная мера степени объективной возможности этого события. Первым по времени определением вероятности следует считать классическое, которое возникло из анализа азартных игр и применялось вначале интуитивно.
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 288. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Элементы комбинаторики.
Элементы комбинаторики. способами, а другой объект В может быть выбран из той же совокупности
способами, а другой объект В может быть выбран из той же совокупности 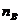 способами, то выбор одного из объектов А или В может быть осуществлён
способами, то выбор одного из объектов А или В может быть осуществлён 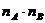 способами.
способами. способов.
способов. ).
). и определяется формулой:
и определяется формулой:

 и вычисляют по формуле:
и вычисляют по формуле:



 , вычисляют:
, вычисляют:






 раз, 2-й -
раз, 2-й -  раз,…, k-й -
раз,…, k-й -  раз, (причём
раз, (причём 

 - выпадение i очков.
- выпадение i очков. - полная группа событий.
- полная группа событий. .
. .
. 
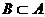 , то события называются эквивалентными (или равными) А=В.
, то события называются эквивалентными (или равными) А=В. , которое происходит тогда и только тогда, когда событие А не происходит.
, которое происходит тогда и только тогда, когда событие А не происходит.


 - при n выстрелах хотя бы одно попадание.
- при n выстрелах хотя бы одно попадание. (А и В), которое происходит тогда и только тогда, когда происходят оба события одновременно.
(А и В), которое происходит тогда и только тогда, когда происходят оба события одновременно.