
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Последовательность проектного расчета закрытой передачиСтр 1 из 7Следующая ⇒ ЛЕКЦИЯ 4 Конические зубчатые передачи Коническая передача состоит из двух конических зубчатых колес (рис.1) и служит для передачи крутящего момента между валами с пересекающимися осями под углом Колеса конических передач выполняют с прямыми (рис.2, а), косыми (рис.2, б), круговыми зубьями (рис.2, в).
а). б). в). Рис.1. Коническая передача Рис.2. Конические колеса Геометрические параметры конического зубчатого колеса Для конических колес различают размеры средние, внешние и внутренние (рис.3). Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом е. Размеры в среднем сечении сопровождают индексом m. Размеры по внешнему торцу удобнее для измерения, их указывают на чертежах. Размеры в среднем сечении используют при силовых расчетах.
 Рис.3. Геометрические параметры конического зубчатого колеса Основные геометрические параметры конической прямозубой передачи
Передаточное отношение конической передачи: Проектный расчет конической передачи Основной задачей проектного расчета конической передачи является определение внешнего делительного диаметра Последовательность проектного расчета закрытой передачи 1. Определить передаточное отношение u. Номинальные значения передаточных отношений (от u = 1 до u = 6,3) и углы делительных конусов шестерни и колеса 2. В зависимости от условий работы передачи выбрать материалы колес, назначить термическую обработку и значения твердости рабочих поверхностей зубьев. 3. Определить внешний делительный диаметр колеса
где 4. Задать число зубьев шестерни z1, определить число зубьев колеса z2 Число зубьев меньшего колеса рекомендуется z1 = 18...30. 5.Рассчитать внешний модуль 6. Определить числа зубьев эквивалентных колес: zV1 и zV2: zv1 = z1/ cosδ1, zv2 = z2/ cosδ2 и по справочным таблицам - коэффициенты формы зуба шестерни YF1 и колеса YF2. 7. Выбрать коэффициент 8. Произвести геометрический расчет передачи (см. табл.). |
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 399. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . Наиболее распространена в машиностроении коническая передача с углом между осями
. Наиболее распространена в машиностроении коническая передача с углом между осями  =900 (рис. 1), но могут быть передачи и с
=900 (рис. 1), но могут быть передачи и с  900 . Конические зубчатые передачи по сравнению с цилиндрическими имеют большую массу и габариты, сложнее в изготовлении и монтаже, так как требуют точной фиксации осевого положения зубчатых колес.
900 . Конические зубчатые передачи по сравнению с цилиндрическими имеют большую массу и габариты, сложнее в изготовлении и монтаже, так как требуют точной фиксации осевого положения зубчатых колес. При окружных скоростях до 2… 3 м/с применяют конические колеса с прямыми зубьями, при больших скоростях используют колеса с круговыми зубьями, которые обеспечивают более плавное зацепление и имеют большую нагрузочную способность и проще в изготовлении.
При окружных скоростях до 2… 3 м/с применяют конические колеса с прямыми зубьями, при больших скоростях используют колеса с круговыми зубьями, которые обеспечивают более плавное зацепление и имеют большую нагрузочную способность и проще в изготовлении.

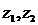

 ,
, 
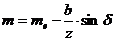
 ,
, 
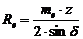



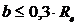
 . (1)
. (1) колеса.
колеса.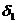 и
и  .
. , (2)
, (2) коэффициент концентрации нагрузки. Принимают 1,1…1,2.
коэффициент концентрации нагрузки. Принимают 1,1…1,2. и средний модуль
и средний модуль  .
. длины зуба.
длины зуба.  .
.