
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Начала термодинамики и их применениеНачалами термодинамики называют постулаты (законы), которые были эмпирически установлены на основе многовековых наблюдений. Существует 5 начал ТД. Первый постулат ТД
Первый постулат называют общим началом термодинамики (о существовании состояния ТД равновесия): у изолированной ТД системы существует состояние термодинамического равновесия, в которое она переходит с течением времени и никогда самопроизвольно из него не выходит.
Второй постулат ТД
Второй постулат называют нулевым началом термодинамики (о существовании связи между параметрами): в состоянии термодинамического равновесия существует функциональная связь между макропараметрами, т. е. при изменении хотя бы одного из равновесных параметров меняются и другие. Эта связь математически (количественно) выражается в виде уравнения состояния вещества. Уравнения состояния бывают: • термические (связь между p, V и T), • калорические (связь между p, V, T и U). Для идеального газа термическим уравнением состояния служит уравнение Менделеева – Клапейрона
или
Оно содержит в себе в виде частных случаев все газовые законы (законы идеального газа). 1. Закон Авогадро: если давления, объемы и температуры газов одинаковые, то газы содержат одинаковое число молекул
2. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений компонент смеси
3. Закон Бойля-Мариотта: при изотермическом процессе давление идеального газа обратно пропорционально его объёму
Зависимость p(V) на координатной плоскости (p,V) изображается гиперболой, которая называется изотермой (рис.):  Давление есть сила, с которой все молекулы действуют на поверхность. Единицей измерения давления в СИ является паскаль:
На практике значение давления измеряют с помощью специальных приборов – барометров.
4. Закон Гей-Люссака: при изобарном процессе объём идеального газа прямо пропорционален его температуре
Зависимость V(T) на плоскости (V,T) изображается прямой, которая называется изобарой, выходит из начала координат и имеет тангенс угла наклона (рис.).
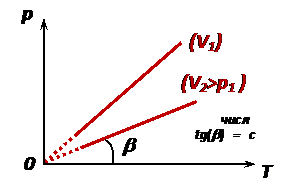
5. Закон Шарля: при изохорном процессе давление идеального газа прямо пропорционально его температуре
Зависимость p(T) на плоскости (p,T) изображается прямой, которая называется изохорой, выходит из начала координат и имеет тангенс угла наклона (рис.):
Для реального газа термическим уравнением состояния служит уравнение Ван-дер-Ваальса
В отличие от уравнения Менделеева - Клапейрона, оно содержит поправки к давлению, оказываемому газом на стенки сосуда, и к объёму сосуда, занимаемому газом. Поправка «внутреннее давление» учитывает действие сил притяжения, которые препятствую разбеганию частиц после столкновения на далёкие расстояния и обеспечивают самосжатие газа. В реальном газе давление на стенки сосуда несколько меньше, чем в идеальном; эта поправка равна
где а – постоянная Ван-дер-Ваальса, характерная для данного газа,
Поправка «собственный объём» учитывает действие сил отталкивания, препятствущих сближению молекул на расстояния, меньшие эффективного диаметра. Доступный объём для движения частиц оказывается меньше, чем в идеальном газе:
Множитель «4» обусловлен наибольшей вероятностью попарных столкновений молекул, b – постоянная Ван-дер-Ваальса, характерная для данного газа,
Следовательно,
На изотермах Ван-дер-Ваальса: • газообразные состояния соответствуют участкам с параметрами
• жидкость соответствует участкам с параметрами
•
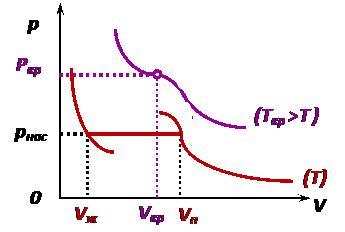
Теоретические изотермы Ван-дер-Ваальса в целом удовлетворяют экспериментально полученным изотермам Эндрюса (рис.), кроме физически невозможных участков, на которых одновременно при сжатии вещества падаем давление. Критические параметры определяются по формулам:
Состояние с критическими параметрами называют «критическим», т. к. если параметры превышают критические, реальный газ невозможно сжать до жидкого состояния. При этом критическая температура выше температуры кипения. Например:
Для идеального газа калорическим уравнением состояния служит уравнение, в котором внутренняя энергия газа из молекул определённого типа зависит лишь от температуры
Внутренняя энергия идеального газа равна сумме кинетических энергий всех его N частиц, поскольку
В случае реального газа калорическим уравнением состояния служит уравнение, в котором внутренняя энергия газа из молекул определённого типа зависит не только от температуры, но и отобъёмавещества.
Это обусловлено тем, что молекулы после столкновения взаимодействуют с силами притяжения, т. е. есть потенциальная энергия. Работа сил притяжения равна
(a – постоянная Ван-дер-Ваальса, n - количество вещества). Внутренняя энергия реального газа зависит и от кинетической энергии частиц (температуры), и от потенциальной энергии взаимодействия частиц (объёма вещества):
Таким образом, статистический смысл величины «внутренняя энергия вещества» состоит в том, что она равна сумме 1) кинетической энергии хаотического поступательного и вращательного движения молекул; 2) потенциальной энергии взаимодействия молекул на расстояниях (притяжение); 3)потенциальной и кинетической энергий колебательного движения атомов в молекулах.
Третий постулат ТД
Третийпостулат называют первым началом термодинамики (о существовании способов изменения внутренней энергии): существует два способа изменения внутренней энергии ТД системы - передача (сообщение или отнятие) теплоты и совершение работы внешними системами над данной системой
Количество теплоты и работа являются способами изменение внутренней энергии, поэтому имеют различные значения в разных процессах, т. е. характеризуют не состояние системы, а процесс изменения состояния. Рассмотрим первое начало термодинамики в применении к различным процессам в идеальном газе. Изохорный процесс – это процесс при неизменном объёме вещества:
В этом случае ТД система работу не совершает:
Тогда всё отдаваемое системе (или отбираемое) количество теплоты при изохорном процессе идёт только на изменение её внутренней энергии (кинетической энергии):
Поскольку
то С точки зрения классической теории теплоёмкости молярная изохорная теплоёмкость не зависит от температуры, определяется лишь числом степеней свободы и является постоянной величиной для данного газа. В частности,
Изобарный процесс – это процесс при неизменном давлении вещества:
В этом случае ТД система совершает работу:
Тогда всё отдаваемое системе (или отбираемое у системы) количество теплоты при изобарном процессе идёт на изменение её внутренней энергии совершение системой работы против окружающей среды:
Поскольку
то С точки зрения классической теории теплоёмкости молярная изобарная теплоёмкость не зависит от температуры, определяется лишь числом степеней свободы и является постоянной величиной для данного газа. При этом
и справедливо уравнение Мáйера:
В частности,
Изотермический процесс – процесс при неизменной температуре вещества:
В этом случае ТД система совершает работу:
Поскольку внутренняя энергия не меняется
то всё отдаваемое системе (или отбираемое у системы) количество теплоты при изотермическом процессе идёт только на совершение системой работы против окружающей среды:
При этом с точки зрения классической теории теплоёмкости молярная изотермическая теплоёмкость бесконечно велика:
Адиабатическим называют процесс, протекающий без теплообмена между ТД системой (веществом) и окружающей средой
Тогда
т. е. при адиабатическом процессе работа ТД системы над окружающей средой происходит за счёт убыли внутренней энергии системы:
Поскольку
то работа равна
Молярная адиабатическая теплоёмкость равна нулю:
Адиабатический процесс является изоэнтропийным (энтропия не меняется):
Все другие параметры {p, V, T} меняются. Их взаимосвязь выражается уравнением Пуассона (в разных переменных):
Величина g называется коэффициентом Пуассона (показатель адиабаты) и равна
В частности,
следует, что адиабата на координатной сетке (p, V) «круче» изотермы (рис.). Теоретическое рассмотрение теплоёмкостей всех процессов показало, что они не зависят от температуры. Однако опыты свидетельствуют, что при охлаждении вещества его теплоёмкость уменьшается и в пределе при абсолютном нуле температуры стремится к нулю. Это привело к необходимости создания новой теории теплоёмкости – квантовой теории – для области низких температур. Классическая МКТ и ТД оказываются не справедливыми при исследовании веществ с очень низкими температурами.
Четвёртый постулат ТД Четвёртый постулат называют вторым началом термодинамики (о существовании и неубывании энтропии): в состоянии термодинамического равновесия у системы существует макропараметр энтропия, которая в случае адиабатически изолированной системы (нет обмена теплотой) не убывает
Для обратимого (равновесного) процесса в изолированной системе энтропия не меняется
Для необратимого (неравновесного) процесса в изолированной системе энтропия возрастает
Согласно второму началу ТД в виде полученного неравенстваКлаузиуса, необратимый процесс в изолированной системе всегда происходит в определённом направлении так, что энтропия системы не убывает:
При этом термодинамическая трактовка изменения энтропии – суммарная приведённая теплота. Однако термодинамика не рассматривает микроскопическое строение вещества, поэтому для более глубокого понимания смысла 2 НТД следует обратиться к статистической трактовке энтропии. Л. Больцман выдвинул гипотезу: между термодинамической вероятностью макросостояния системы и её энтропией существует однозначная связь. Он доказал, что эта связь имеет вид уравнения Больцмана: Термодинамическая вероятность – это число способов реализации данного макросостояния системы, т. е. число микросостояний, обусловленных движением и «перестановкой» частиц. Когда система находится в состоянии равновесия, то: - частицы равномерно (равновероятно) распределены, - число микросостояний системы (термодинамическая вероятность) максимально - энтропия системы максимальна Таким образом: • энтропия есть мера беспорядка, хаоса; • наиболее вероятными процессами в природе являются самопроизвольные процессы перехода в состояние равновесия и беспорядка с максимальной энтропией. Однако в системе многих частиц всегда есть флуктуации, отклонения от общих закономерностей. Они становятся более существенными в системах небольшого числа частиц. Поэтому процесс роста энтропии оказывается лишь более вероятным, и есть вероятность процессов с уменьшением энтропии. Пятый постулат ТД Пятыйпостулат называют третьим началом термодинамики или тепловой теоремой Нернста (о существовании и недостижимости абсолютного нуля температуры): при приближении к абсолютному нулю температуры энтропия любой ТД системыперестаёт зависеть от каких-либо ТД параметров и принимает одно и то же постоянное значение
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 316. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
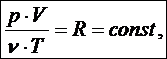
 .
.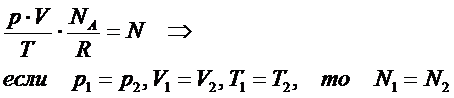
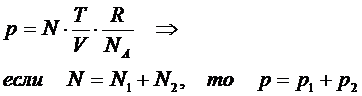

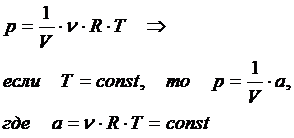
 .
.
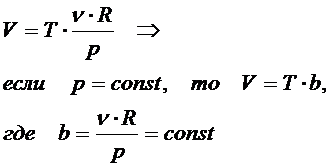

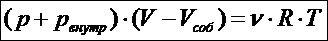 .
.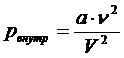
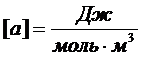 .
.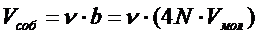 .
.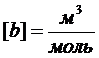 .
.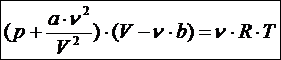 .
.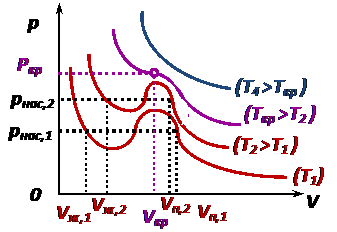 Уравнение Ван-дер-Ваальса позволяет описывать фазовый переход «газ ↔ жидкость», что невозможно было сделать на основе уравнения состояния идеального газа (рис.).
Уравнение Ван-дер-Ваальса позволяет описывать фазовый переход «газ ↔ жидкость», что невозможно было сделать на основе уравнения состояния идеального газа (рис.).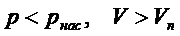 ;
;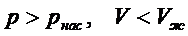 ;
; двухфазные состояния соответствуют участкам с параметрами
двухфазные состояния соответствуют участкам с параметрами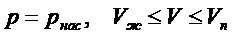
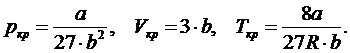
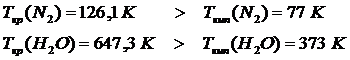
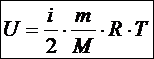 .
.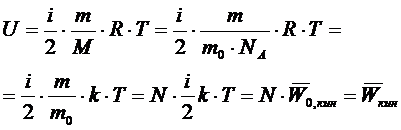
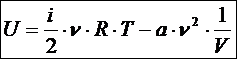 .
.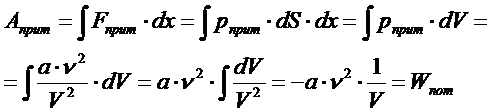
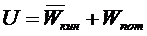
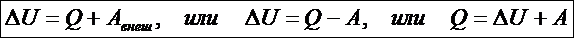 ,
,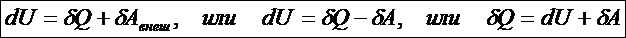 .
.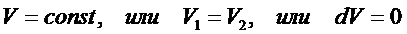
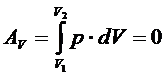
 .
. ,
,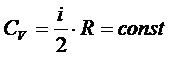


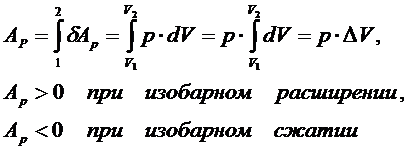
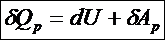
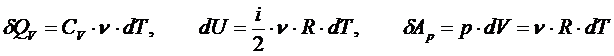 ,
,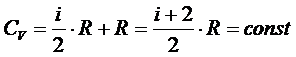
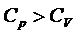
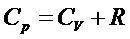 .
.
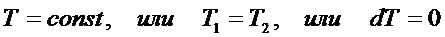
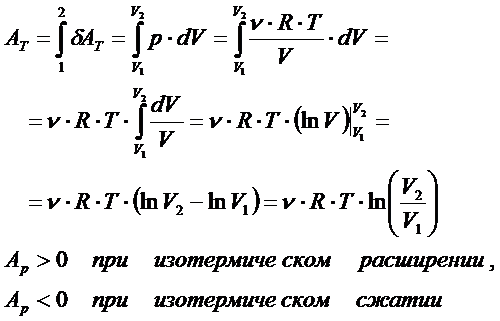
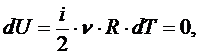
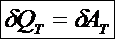
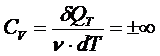
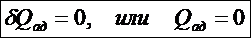

 .
.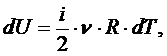

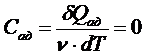
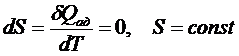
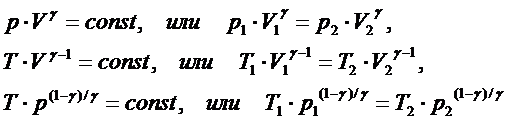


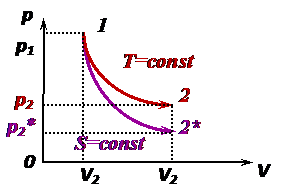 Из сравнения уравнения Пуассона в переменных (p, V) и уравнения Бойля – Мариотта (для изотермического процесса) с учётом
Из сравнения уравнения Пуассона в переменных (p, V) и уравнения Бойля – Мариотта (для изотермического процесса) с учётом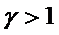
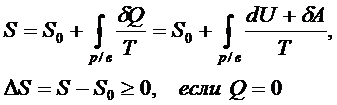
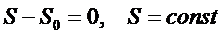 .
.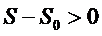 ,
, 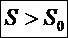 .
.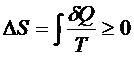
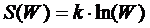
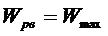
 .
.