
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Частицы взаимодействуют друг с другом
Силами взаимодействия являются силы Ван-дер-Ваальса – силы притяжения и отталкивания. Они существенно, но по-разному зависят от расстояния между частицами (рис.):
• На далёких расстояниях между частицами силы притяжения и отталкивания пренебрежимо малы (рис.), и частицы движутся равномерно, без ускорений
• При сближении частиц силы Ван-дер-Ваальса возрастают (рис.), при этом притяжение преобладает над отталкиванием:
• При дальнейшем сближении силы отталкивания существенно возрастают (рис.), компенсируя силы притяжения (энергия взаимодействия частиц минимальная):
• На малых расстояниях между частицами силы отталкивания преобладают над силами притяжения (рис.), и происходит столкновение частиц – они не могут сблизиться на расстояние, меньшее эффективного диаметра
Частицы совершают тепловое движение
Тепловое движение – это непрерывное хаотическое движение частиц, которые сталкиваются друг с другом случайным образом. Во время столкновения силы отталкивания заставляют частицы «разлетаться», при этом у каждой частицы изменяются (рис.): • модуль и направление скорости (по закону сохранения импульса), • кинетическая энергия, • пройденный путь до следующего столкновения. •
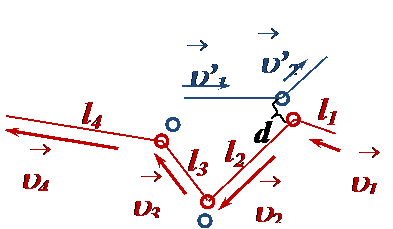
После столкновения силы Ван-дер-Ваальса быстро убывают, и движение молекул можно считать равномерным, «свободным». Случайность столкновений (вероятностный процесс) означает, что длина свободного пробега (пути) между столкновениями, скорость и кинетическая энергия любой молекулы являются случайными величинами. Поэтому физический смысл имеют средние значения этих величин.  • Средняя длина свободного пробега молекулы
Вакуум - это состояние газа, в котором средняя длина свободного пробега частиц сопоставима и больше линейных размеров сосуда, т. е. частицы практически не сталкиваются друг с другом. Понятие вакуума относительно: чем больше характерный размер сосуда, тем при меньшем давлении наступает состояние вакуума, и наоборот. Например, для воздуха в пористых телах с диаметром пор менее 10-7 м (< 0,1 мкм), состояние воздуха можно считать вакуумом даже при атмосферном давлении. • Средняя арифметическая скорость молекулы
(f(u) – плотность вероятности, определяемая функцией Максвелла)
• Средняя квадратичная скорость молекулы
• Средняя кинетическая энергия молекулы
Основные законы теплового движения Основное уравнение МКТ
Взаимосвязь макро- и микропараметров называется основным уравнением молекулярно-кинетической теории строения вещества. Основное уравнение МКТ идеального газа устанавливает количественное соотношение между давлением газа на стенки сосуда (макропараметр) и средней квадратичной скоростью или средней кинетической энергией молекулы (микропараметр)
Теорема о равнораспределении энергии
Молекулы газа в общем случае (реальный газ) могут двигаться не только поступательно, но и вращаться, а также существует колебательное движение атомов в молекуле. Поэтому число степеней свободы (возможных движений) равно
Теорема о равнораспределении средней кинетической энергии по степеням свободы: на каждую степень свободы приходится средняя кинетическая энергия
(k – постоянная Больцмана). Частные случаи (рис. 4): 1) если молекула газа одноатомная, то
2) если молекула газа «жёсткая» двухатомная, то
3) если молекула газа «жёсткая» трёх- и многоатомная, то
Температура – мера энергии
Из теоремы о равнорапределении энергии следует, что термодинамическая температура служит мерой кинетической энергии. При охлаждении вещества сначала «замораживаются» поступательные степени свободы – газ переходит в жидкость, уменьшается число «кочующих» молекул, увеличивается число «осёдлых». При дальнейшем охлаждении «замораживаются» вращательные степени свободы – жидкость превращается в твёрдое тело, частицы которого преимущественно колеблются около положений равновесия. В пределе – при абсолютном нуле температуры – движение молекул прекращается с точки зрения классической физики. На такой трактовке температуры была построена теоретическая шкала Кельвина – термоднамическая шкала:
Практически применяют эмпирическую шкалу Цельсия:
Однако даже при «абсолютном» нуле термодинамической температуры остаётся внутриатомное, внутриядерное и др. движения, описываемые квантовой физикой, и выводы классической физики на основе МКТ теряют прежний физический смысл. 4.1.3. Статистические распределения молекул Распределение Максвелла
Молекулы вещества при одной той же температуре движутся с разными скоростями. Распределение молекул по скоростям или кинетическим энергиям называется распределением Максвелла и имеет вид (рис.):
Плотность вероятности (функция Максквелла)
показывает, какая доля молекул от общего их числа (т. е. вероятность) движется со скоростями в заданном интервале значений скоростей: 1) Доля медленных молекул мала
2) Доля быстрых молекул мала
3) Большинство молекул движется с наивероятнейшейскоростью
Распределение Максвелла: - справедливо для равновесного состояния газа (с постоянной температурой), т. е. при отсутствии явлений переноса; - не учитывает действие внешних потенциальных полей (поле силы тяжести).
Распределение Больцмана
Полем силы тяжести нельзя пренебрегать. Оно влияет на концентрацию молекул в зависимости от удаления от поверхности Земли. Это влияние описывает распределение Больцмана – распределение молекул по потенциальным энергиям (рис.):
Поскольку
то справедлива и барометрическая формула
Распределение Больцмана и барометрическая формула выполняются: - для равновесного состояния газа (с постоянной температурой), т. е. при отсутствии явлений переноса, - для нижнего слоя атмосферы (тропосферы), имеющего толщину 10 - 11 км, поскольку в пределах этого слоя можно пренебречь зависимостью изменением ускорения свободного падения от высоты.
Вследствие закона сохранения энергии, оба распределения можно объединить в общее, которое называется распределением Максвелла – Больцмана, также справедливое для равновесного состояния газа. Термодинамика 4.2.1. Основные понятия термодинамики Термодинамическая система – система огромного числа частиц (атомов, молекул), способная обмениваться своим веществом и энергией с другими системами. Термодинамическое состояние – способ существования ТД системы, который характеризуется ТД параметрами. Состояния бывают: • равновесные – неизменные с течением времени, причём при постоянных внешних условиях внутри системы нет потоков (явлений переноса); на координатных сетках (p, V), (V,T), (p,T), (S,T) изображаются точками; • неравновесные состояния характеризуются явлениями переноса, после прекращения которых переходят в равновесные. Термодинамические параметры (макропараметры) – физически величины, описывающие состояние ТД системы в целом (объём, температура, давление, внутренняя энергия, энтропия и др.). В равновесном состоянии они имеют постоянные значения. Термодинамические процессы – переходы из одного ТД состояния в другое. Процессы бывают: • равновесные – достаточно медленные процессы перехода между равновесными состояниями (в газах: изотермический, изобарический, изохорический); на координатных сетках (p, V), (V,T), (p,T), (S,T) изображаются сплошными линиями; • неравновесные – сравнительно быстрые процессы перехода между неравновесными состояниями (в газах: адиабатический); на координатных сетках (p, V), (V,T), (p,T), (S,T) нельзя изобразить линиями. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 347. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
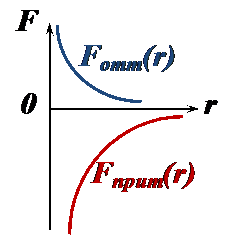
 ,
, ,
, 
 Рассмотрим зависимость сил Ван-дер-Ваальса от расстояния между частицами газа.
Рассмотрим зависимость сил Ван-дер-Ваальса от расстояния между частицами газа.
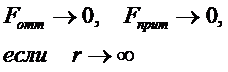 .
.
 .
.
 .
. .
. направление траектории (в течение некоторого времени наблюдения она приобретает вид ломаной линии из отрезков разной длины).
направление траектории (в течение некоторого времени наблюдения она приобретает вид ломаной линии из отрезков разной длины).
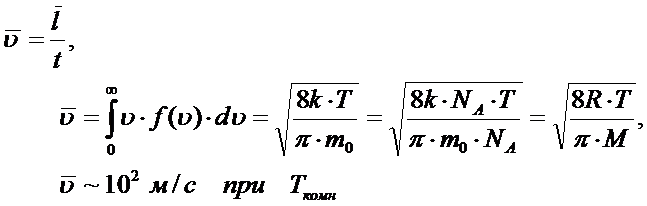




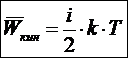










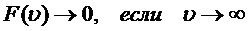


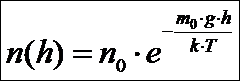

 или
или 